حذف نویز از سیگنال دیجیتالی با فیلتر در متلب - انجام پروژه متلب |پروژه متلب | انجام پروژه متلب برق | شبیه سازی با متلب

حذف نویز از سیگنال دیجیتالی با فیلتر در متلب

حذف نویز از سیگنال دیجیتالی با فیلتر در متلب :پروژه متلب

پروژه متلب :

روشهاي مختلف حذف نويز

روشهاي مختلف حذف نويز سيگنالهاي ديجيتال به دو دسته کلي کلاسيک و غيرکلاسيک تقسيم ميشوند.

روشهای کلاسيک شامل تفريق طيف، فيلتر وينر و فیلترهای تطبيقي ميباشند.

در روش غيرکلاسيک، از ايده عبور از آستانه با استفاده از تبديل ويولت و يا تبديل  کسينوس استفاده مي شود.

روشهاي فوق همگي عمومي بوده و براي کليه سيگنالهاي يک بعدي قابل اعمال هستند. فرض خاصي روي مشخصات سيگنال نشده، ولي در تمام کار نويز در نظر گرفته شده، گوسي با متوسط صفر است.

تا حد امکان تلاش شده کيفيت عملکرد روشهاي مختلف با معيار SNR که نسبت سیگنال به نویز می باشد نشان داده شود.

می دانیم که هرچه مقدار عددی SNR بیشتر باشد سیگنال دارای نویز کمتری می باشد.در روش کلاسیک همانطور که از اسم آن پیداست با عبور سیگنال از فیلترهای ذکرشده سیگنال خروجی را بدست می اوریم که فرایندی ماشینی می باشد و ایده ای برای بهبود آن به طور چشمگیر وجود ندارد.

اما در روش غیر کلاسیک می توان از الگوریتم های بهبود یافته برای حذف نویز استفاده کرد،مثلا برای حذف نویز در سیگنال می توان ار روش میانگین گیری از نمونه های اطراف استفاده کرد که روش های متفاوتی برای این کار با SNR های متفاوت موجود می باشد که در این پروژه به دو مورد از آنها اشاره خواهیم کرد.

پروژه متلب : در هر کدینگ دیجیتالی، یک محدوده مشخص به دو قسمت تقسیم می‌شود. قسمتی به نام ولتاژ بالا (High Voltage یا HV) و قسمتی به نام ولتاژ پایین (Low Voltage یا LV) شناخته می‌شود. اگر ولتاژ سیگنال در محدوده High Voltage باشد، حالت آن سیگنال به عنوان یک منطقی و اگر در محدوده Low Voltage باشد حالتش صفر منطقی خواهد بود.

در تکنولوژی‌های مختلف مدارات دیجیتالی، قراردادی که برای HV و LV تعیین کرده اند متفاوت است مثلاً در مدارات CMOS که در کامپیوتر استفاده می‌شوند، محدوده LV از صفر ولت تا ولتاژ تغذیه تقسیم بر ۲ و محدوده HV از ولتاژ تغذیه تقسیم بر ۲ تا خود ولتاژ تغذیه است یعنی اگر ولتاژ تغذیه ۵ باشد، از ۰ تا ۲.۵ ولت به عنوان صفر منطقی و از ۲.۵ تا ۵ ولت به عنوان یک منطقی شناخته خواهد شد.

یک نمودار ایده‌آل برای سیگنال‌های دیجیتالی مانند عکس زیر خواهد بود:

پروژه متلب : با این حال در عمل چنین نموداری حاصل نمی‌شود. به دلیل نویزهای موجود، معمولاً ولتاژ کمی تغییر می‌کند ولی به دلیل قرار داد موجود، همچنان صفر و یک منطقی به درستی تشخیص داده می‌شود. برای مثال در تصویر زیر می‌توانید سیگنال‌های دیجیتالی با نویز نسبتاً زیاد را ببینید که ۰ و ۱ شان هم نشان داده شده است:

یک مثال کاربردی

پروژه متلب : برای درک بیشتر نحوه عملکرد این دو نوع سیگنال، فرض کنید که قصد ضبط صدا، ذخیره کردن آن و پخش صدای ذخیره شده را داشته باشیم.

برای ضبط کردن صدا از یک میکروفون استفاده می‌کنیم که بسته به ضربه صوتی‌ای که به آن زده می‌شود، سیگنال‌های آنالوگی را تولید می‌کند که برابر صدای دریافتی است. ما نمی‌توانیم آنالوگ را بر روی حافظه‌های جانبی ذخیره کنیم چون مثلاً هارد دیسک، در هر مکان ذخیره داده مثل یک آهنربا دو حالت دارد: یا S به سمت ما است یا N یعنی یا صفر یا یک. در حافظه‌های فلش نیز چنین است یا ترانزیستورها به اصطلاح باز اند یا بسته یعنی یا صفر یا یک. حتی در قدیمی ترین حافظه‌ها مثل کارت‌های سوراخ دار هم دو حالت وجود دارد یا مکان حافظه داده‌ها سوراخ است یا نیست یعنی باز هم یا یک یا صفر.

حافظه‌های جانبی می‌توانند داده‌های دیجیتالی را ذخیره کنند اما ورودی ما آنالوگ است! در این میان یک مبدل آنالوگ به دیجیتال، داده‌های آنالوگ را معادل سازی کرده و در قالب دیجیتال به حافظه جانبی می‌فرستد و در آن جا به عنوان صفر و یک های منطقی ذخیره می‌شوند.

در هنگام پخش صدا نیز داده‌های باینری از روی حافظه خوانده شده و به چیپی که وظیفه تبدیل داده‌های دیجیتالی به آنالوگ را دارد، تحویل داده می‌شود. حال که داده‌هال آنالوگ صدا در اختیار ماست، کافیست با استفاده از یک تقویت کننده صدا را بلند تر کرده و به اسپیکر یا هر خروجی صدای دیگری ارسال کنیم. در اسپیکر هم لرزاننده هوا با توجه به قدرت سیگنال آنالوگ در لحظه، به هوا ضربه وارد کرده و در نتیجه به گوش ما می‌رسد.

تبدیل سیگنال آنالوگ به دیجیتال (Analog to Digital Conversion)

نمونه‌برداری (Sampling)

پروژه متلب :  بر اساس قضیه نمونه‌برداری نایکوییست-شانون (Nyquist-Shannon Sampling Theorem)، اگر از یک سیگنال پیوسته با بسامدی دست کم دو برابر بسامد بیشینه آن نمونه‌برداری کنیم، می‌توانیم با استفاده از مقادیر نمونه‌برداری شده، سیگنال اصلی را دقیقاً بازسازی کنیم. به این مقدار بسامد، بسامد نایکویست گفته می‌شود. حاصل نمونه‌برداری از سیگنال پیوسته را سیگنال گسسته می‌گویند (البته گسسته در زمان ولی پیوسته در دامنه).

مقداردهی یا کوانتش (Quantization)

برای دیجیتال کردن سیگنال گسسته (در زمان) که در واقع دارای دامنۀ پیوسته است، باید آن را از نظر دامنه هم گسسته کرد (مقادیر دامنه آن را هم به مقادیر خاصی محدود کرد). به این کار، مقداردهی (کوانتش) می‌گویند. دلیل کوانتش آن است که مقادیر پیوستۀ نمونه‌ها را نمی‌توان ذخیره کرد.

دیجیتال‌سازی (Digitization)

پروژه متلب : مقادیر کوانتیده (quantized) سیگنال را می‌توان به دیجیتال (یعنی به رشتهٔ صفر و یک) تبدیل کرد. با این کار، سیگنال دیجیتال به‌دست می‌آید.

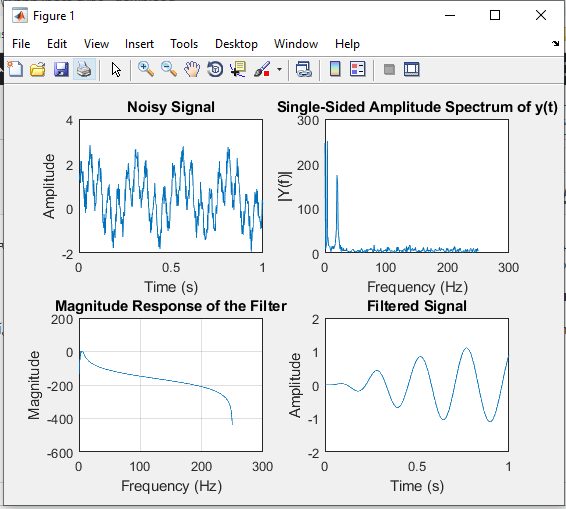
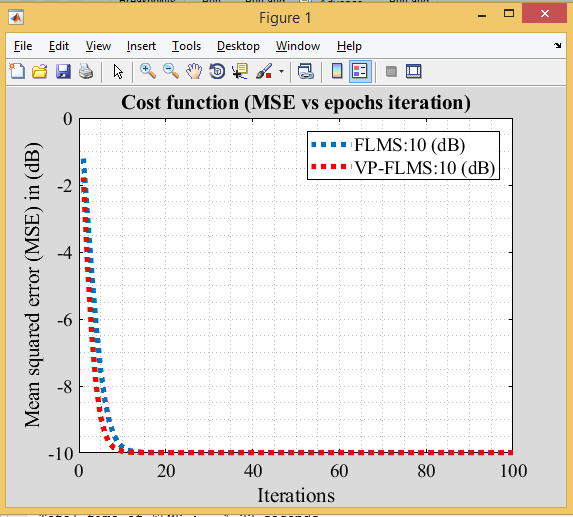
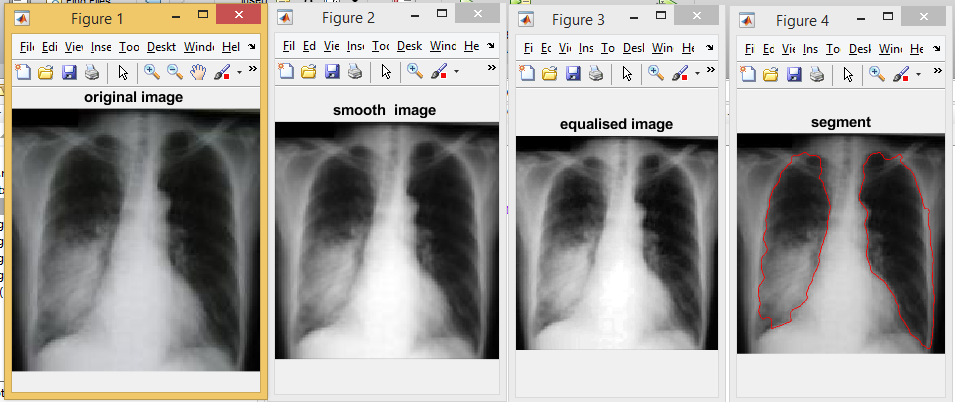
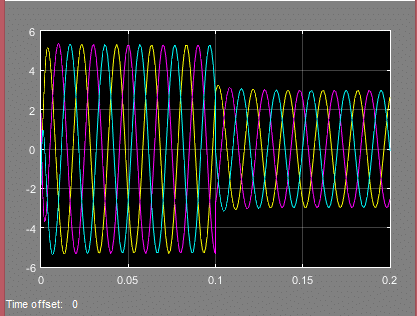
خروجی متلب: