تشخیص دایره با کمک تبدیل هاف و پردازش تصویر در متلب
تشخیص دایره با کمک تبدیل هاف و پردازش تصویر در متلب :پروژه متلب
در این پروژه با کمک تبدیل هاف پیکسل های تصویر سگمنت گذاری و لبه یابی و به وسیله تبدیل هاف مشخص می گردد.
در ابتدا، تعریف ابتدایی از «تصاویر دیجیتال» (Digital Images) و محیط برنامهنویسی متلب ارائه خواهد شد. سپس، مجموعهای از عملیات ابتدایی پردازش تصویر در متلب مورد بررسی قرار خواهد گرفت. از جمله مهمترین فرایندهای پردازشی مقدماتی روی تصاویر دیجیتال، میتوان به مواردی نظیر «خواندن تصویر» (Image Reading)، «نمایش تصویر» (Image Display) و «ذخیرهسازی تصویر» (Image Storing) اشاره کرد. در ادامه نیز، مجموعهای از توابع پردازش تصویر پیشرفته در متلب مورد بررسی قرار خواهد گرفت و چگونگی استفاده از آنها برای پردازش تصویر در متلب شرح داده خواهد شد.
پروژه متلب یک مشکل رایج در بینایی ماشین تعیین موقعیت، تعداد یا جهت اشیاء خاص در تصویر میباشد. به عنوان مثال مسئله میتواند تعیین جادههای مستقیم در تصاویر هوایی باشد. این مشکل با استفاده از تبدیل هاف برای خطوط قابل حل میباشد. اغلب اشیاء مورد علاقه شکلهایی غیر از خط دارند مثل دایره، بیضی یا هر شکل دلخواه دیگر. با وجود اینکه پیچیدگی تبدیل هاف با افزایش تعداد پارامترهای مورد نیاز برای توصیف شکل مورد نظر افزایش می یابد، تبدیل عادی و عمومی هاف میتواند روی هر نوع شکلی استفاده شود. در ادامه به بررسی تبدیل هاف برای دایره (تبدیل هاف مُدَوَّر) خواهیم پرداخت.
نمایش پارامتری
پروژه متلب تبدیل هاف به عنوان تبدیل یک نقطه در صفحه x-y به فضای پارامتری توصیف میشود. فضای پارامتر بر اساس شکل شیء مورد نظر تعریف میشود. یک خط راست که از نقاط (x1,y1) و (x2,y2) عبور میکند در صفحه x-y با معادله زیر تعریف میشود :
دایره در مختصات کارتِزیَن به صورت زیر بیان میشود:
انباره
پروژه متلب پروسه یافتن دایره در یک تصویر به کمک تبدیل هاف به صورت زیر است : ابتدا تمام لبهها در تصویر مشخص میشوند. این بخش ارتباطی به تبدیل هاف ندارد و هر تکنیک تشخیص لبه دلخواه مثل سوبل یا کَنی یا هر عمل ریختشناسی دیگر میتواند مورد استفاده قرار گیرد.
سپس در هر نقطه لبه یک دایره به مرکزیت نقطه مورد نظر با شعاع دلخواه ترسیم میشود. این دایره در فضای پارامتری طوری ترسیم میشود که محور x مؤلفه a و محور y مؤلفه b و محور z شعاع دایره را مدل میکند. در مختصاتی که متعلق به محیط دایره ترسیم شده هستند، مقدار ماتریس انباره که اندازهای برابر با فضای پارامترها دارد، افزایش داده میشود. بدین طریق تمامی نقاط لبه تصویر اصلی با ترسیم دایرهای به شعاع دلخواه و افزایش مقادیر در انباره، بررسی میشوند. پس از این، انباره شامل اعدادی است که بیانگر تعداد دایرههای عبورکننده از یک مختصات منحصربهفرد میباشد. بنابراین اعداد بزرگتر که به صورت هوشمند با توجه به شعاع انتخاب میشوند، متناظر با مراکز دایرههای در تصویر اصلی میباشند.
الگوریتم
پروژه متلب الگوریتم تبدیل هاف دایرهای به صورت زیر خلاصه میشود :
- یافتن لبه ها
- برای هر نقطه لبه : // تبدیل هاف شروع میشود//
- یک دایره با مرکزیت نقطه لبه با شعاع r رسم میشود و در انباره تمام مختصاتی که محیط دایره از آنها عبور میکند، افزایش می یابند.
- نقاط ماکزیمم در انباره پیدا میشود. // تبدیل هاف تمام میشود//
- پارامترهای پیدا شده (r,a,b) مطابق با نقاط ماکزیمم پیدا شده روی تصویر اصلی مشخص میشوند.
پیادهسازی
با توجه به الگوریتم ارائه شده در قسمت ۴ میتوان به پیادهسازی الگوریتم اقدام کرد. ولی قبل از آن چند نکته بایستی مد نظر قرار گیرد.
چگونه دادهها ذخیره میشود؟
آرایه انباره که سه بعدی است، در صورتیکه شعاع ثابت در نظر گرفته نشده باشد، خیلی سریع میتواند از لحاظ اطلاعات ذخیره شده رشد پیدا کند. سایز این آرایه به تعداد شعاعها و مخصوصاً به اندازه تصویر وابسته است. هزینه محاسباتی برای محاسبه کردن تمام دایرههای مربوط به نقاط لبه با افزایش نقاط لبه افزایش می یابد که تعداد نقاط لبه معمولاً تابعی از اندازه تصویر میباشد. زمان کلی محاسبات تبدیل هاف دایرهای در تصاویر بزرگ با نقاط لبه زیاد میتواند به سرعت به مقدار مهار نشدنی از زمان برسد.
چگونه در فضای گسسته دایره رسم میشود؟
پروژه متلب دایره در فضای گسسته با استفاده از رابطه (۴) مستقیماً رسم میشود، اما یک مشکل وجود دارد. چگونه مقادیر گسسته یا وضوح {\displaystyle \theta } انتخاب شود ؟ یک راه حل اینست که وضوح بالای {\displaystyle \theta } استفاده شود و مقادیر گرد شوند. اما این کار سبب ترسیم بیش از یک بار پیکسلهای لبه شده یا اگر شعاع خیلی بزرگ باشد سبب کمبود پیکسلها میشود. راه دیگر گرد کردن sin و cos پس از ضرب مقادیر با شعاع میباشد. برای اطمینان از ترسیم تمام پیکلها، وضوح {\displaystyle \theta } بایستی بسیار بالا باشد، اما این کار سبب افزایش یافتن هزینه محاسباتی میشود. یک روش که میتواند هزینه محاسبات را پایین بیاورد، محاسبه سریع مقادیر برای توابع sin و cos با استفاده از جدول مراجعه میباشد. اگر چه روشهای عنوان شده عملی هستند، ولی راه حلهای بهتری نیز وجود دارد. به جای استفاده از رابطه (۴)، الگوریتم بِرزِنهام را میتوان برای رسم دایره استفاده کرد. این الگوریتم جهت ترسیم خط یا دایره برای مانیتورهای دیجیتالی بدون مشکل ترسیم بیش از یک بار پیکسلها طراحی شده و برای تبدیل هاف دایرهای مناسب میباشد . یک ویژگی خوب در این الگوریتم اینست که میتوان فهمید که تعداد دقیق پیکسلهای مورد استقاده برای ترسیم دایره چقدر است و این اطلاعات زمانی میتواند مناسب باشد که مرکز دایرهها از دادههای انباره پیدا میشوند. کد پیادهسازی این الگوریتم در [] موجود است.
چگون دایره از درون دادههای تبدیل هاف پیدا میشود؟
پروژه متلب اگرچه این بحث مربوط به تبدیل هاف نیست ولی برای استخراج اطلاعات دایرهها از دادههای انباره مفید است. اگر دربارهٔ تعداد دایرهها و شعاعهای آنها اطلاعاتی وجود ندارد، این پروسه خیلی دردسر ساز است. یک رویکرد آنست که قلههای صفحه a و b هر یک متناظر با یک شعاع خاص هستند در انباره داده پیدا شود. اگر ارتفاع قله (ها) در مقایسه با تعداد پیکسلهای لبه مربوط به دایرهای با شعاع خاص برابر باشد، مختصات قله (ها) شاید متناظر مرکز چنین دایرهای باشد. اما مثلاً در حالتی که دایره کامل نباشد یا یک شکل بیضی مانند داشته باشیم، مرکز دایره میتواند با ارتفاعی کمتر از تعداد پیکسلهای لبه نمایش داده شود. در نهایت اگر مشخص کردن دقیق قلهها سخت است، انباره داده را میتوان هموار کرد.
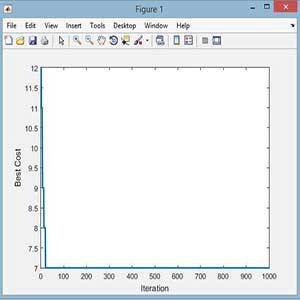
خروجی متلب :

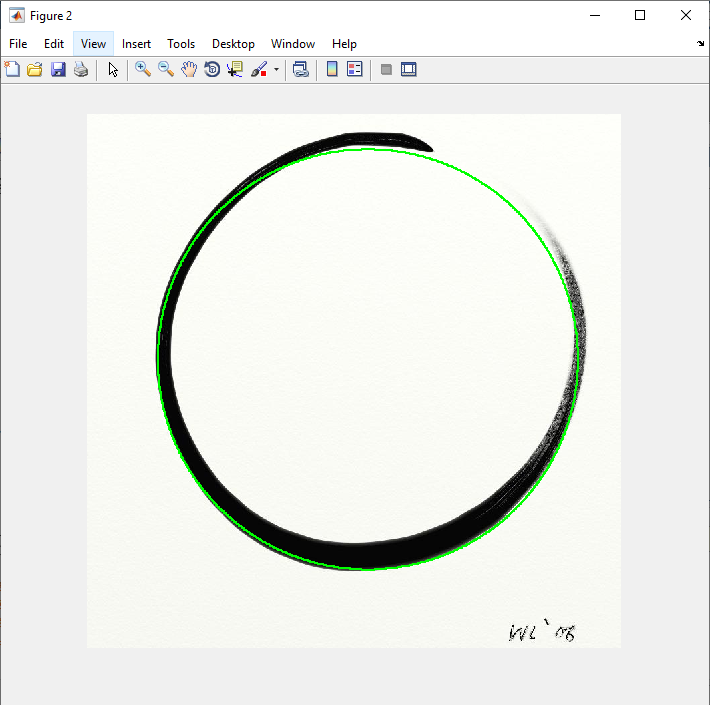
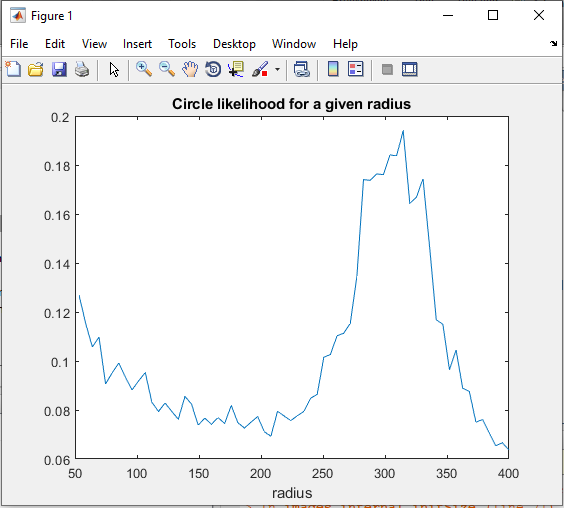

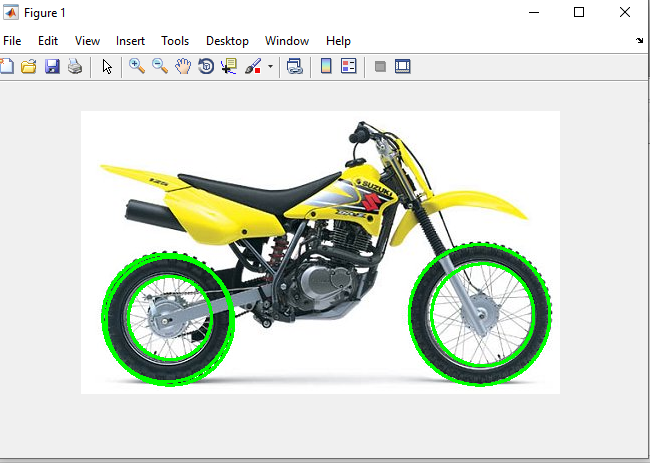










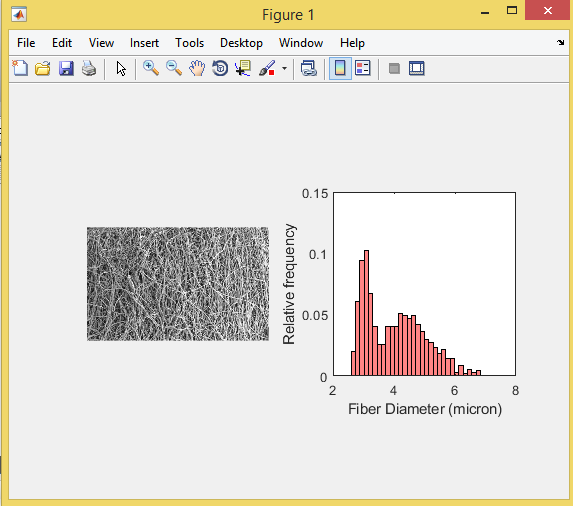


لطفاً براي ارسال دیدگاه، ابتدا وارد حساب كاربري خود بشويد