simulink project
شبیه سازی موتور القایی در سیمولینک متلب : آموزش متلب
چکیده:
آموزش متلب از موتور های DC جهت کنترل سرعت در صنعت فراوان استفاده میشود.بنابراین کنترل
دور موتور DC از اهمیت فراوانی برخوردار است.جهت کنترل دور در این موتور پارامترهای فرکانس
و ولتاژ تغییر داده میشوند.در این پروژه پارامتر مورد نظر ولتاژ میباشد که توسط یک کنترل کننده فازی
کنترل میشود.
شبیه سازی حالت بلوک دیاگرامی
موتوری که ما قصد طراحی آن را داریم یک موتور با توان ۳hp(سه اسب بخار) می باشد که در جدول زیر مشخصات مربوط به آن را مشاهده می نمایید؛
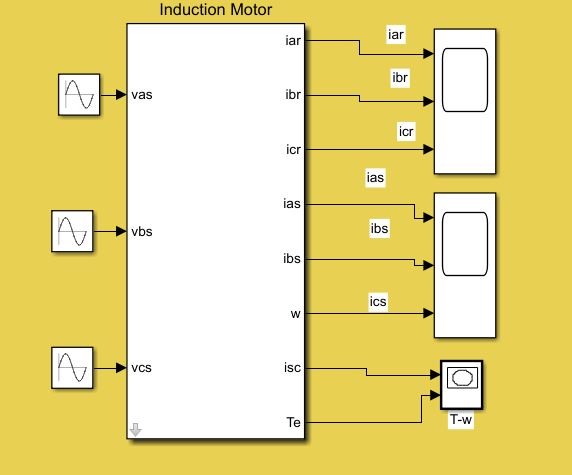
در ابتدا موتور القایی ۳ فاز را به صورت بلوک دیاگرامی طبق روابط ریاضی آن طراحی می کنیم که در زیر تصویر آن قرار داده شده است.
آموزش متلب در نهایت با توجه به ورودی های لازم این بلوک، آن را به ۴ بلوک ویژه سیگنال ورودی متصل می کنیم و از سمت دیگر ۷ خروجی که شامل جریان های سه فاز استاتور، جریان های سه فاز رتور و سرعت موتور می باشد متصل می کنیم.
در نهایت تصویر زیر کل پروژه ما را نشان می دهد؛
البته در نظر داشته باشید که ما هیچ یک از عوامل تلف زا مانند؛ اصطحکاک، مقاومت هوا و … را در نظر نگرفته ایم.
تحلیل حالت بلوک دیاگرامی
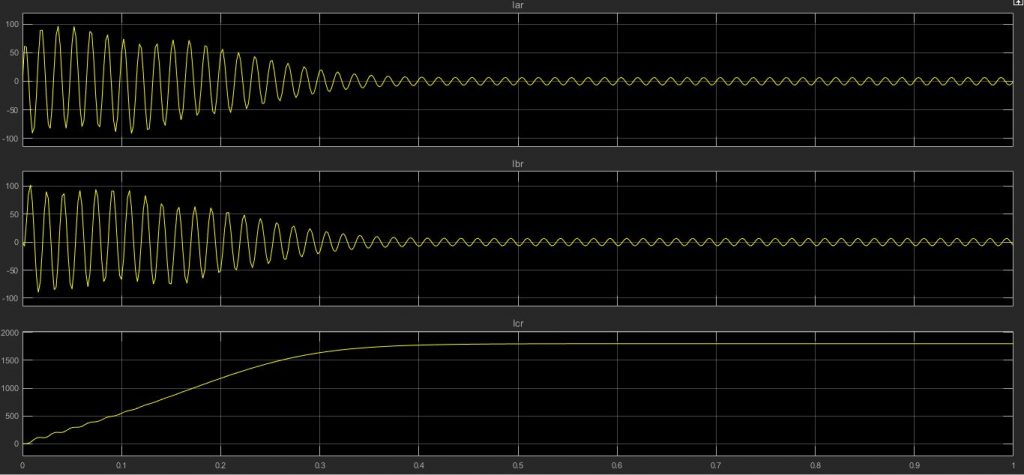
همانگونه که در نمودار های زیر مشاهده می کنید برخلاف تصور نوسانات جریان های استاتور بیشتر از رتور بوده و آموزش متلب حتی در زمان میرا شدن هم شاهد تفاوت زیادی بین این دو جریان هستیم؛ به گونه ای که جریان های رتور نسبت به استاتور زودتر میرا شده اند.
شبیه سازی موتور با M فایل
با توجه به اینکه ماشین های القایی با توان پایین(۳hp) دارای لغزش نسبتا بالایی هستند و به همین دلیل گشتاور نامی در سرعتی خیلی کمتر از سرعت نامی ظاهر می شود قصد داریم با شبیه سازی این موتور این مطلب را در قالب نمودار مشاهده(اثبات) نماییم، و ببینیم در چه سرعتی شاهد گشتاور نامی خواهیم بود.
پس در ابتدا شروع به وارد کردن داده های موتور القایی به صورت زیر می نماییم، توجه داشته باشید که این موتور دقیقا همان موتور شبیه سازی شده در قسمت قبلی می باشد؛
|
۱
۲
۳
۴
۵
۶
۷
۸
۹
۱۰
۱۱
۱۲
۱۳
۱۴
۱۵
۱۶
۱۷
۱۸
۱۹
|
clear all
clc
J=.089;
rr=.816;
t=0;
i=0;
dt=.0001;
P=4;
Tl=11.9/2;
Te=0;
tet0=0;tetr0=0;tet=0;tetr=0;
rs=.435;
Wr0=0;
Xlr=.754;
Xls=.754;
Wb=120*pi;
Xm=26.13;
Xss=Xls+Xm;
Xrr=Xlr+Xm;
|
و سپس طبق معادلات بیان شده برای ماشین القایی به صورت غیرخطی عمل می کنیم و روابط ریاضی را به صورت ماتریسی می نویسیم که در زیر آورده شده اند؛
|
۱
۲
۳
۴
۵
۶
۷
۸
|
D=(Xss*Xrr)–(Xm^2);
vqr=0;vdr=0;vor=0;
Q0=[0;0;0;0;0;0];
Qqs=0;Qds=0;Qos=0;Qqr=0;Qdr=0;Qor=0;
while t<=3 Vas=220*(.8165)*cos(Wb*t); Vbs=220*(.8165)*cos((Wb*t)–(2*pi/3)); Vcs=220*(.8165)*cos((Wb*t)+(2*pi/3)); Ks=(2/3)*[cos(tet0) cos((tet0)–(2*pi/3)) cos((tet0)+(2*pi/3));sin(tet0) sin((tet0)–(2*pi/3)) sin((tet0)+(2*pi/3));.5 .5 .5]; V1=Ks*[Vas;Vbs;Vcs]; vqs=V1(1,1);vds=V1(2,1);vos=V1(3,1); Q=[Qqs;Qds;Qos;Qqr;Qdr;Qor]; V=[vqs;vds;vos;vqr;vdr;vor]; Wr=Wr0; W=Wr; A=[rs*Xrr/D (W/Wb) 0 (–rs*Xm/D) 0 0;(–W/Wb) rs*Xrr/D 0 0 –rs*Xm/D 0;0 0 rs/Xls 0 0 0;–rr*Xm/D 0 0 rr*Xss/D (W–Wr)/Wb 0;0 (–rr*Xm/D) 0 (–(W–Wr)/Wb) rr*Xss/D 0;0 0 0 0 0 rr/Xlr]; B=[1/Wb 0 0 0 0 0;0 1/Wb 0 0 0 0;0 0 1/Wb 0 0 0;0 0 0 1/Wb 0 0;0 0 0 0 1/Wb 0;0 0 0 0 0 1/Wb]; Brev=inv(B); Arev=–inv(B)*A; Q01=Arev*Q+Brev*V; Te=(P/2)*(3/2)*(Xm/(D*Wb))*((Q(1,1)*Q(5,1))–(Q(2,1)*Q(4,1))); Wr01=(P/2)*((Te–Tl)/J); tet01=W; tetr01=Wr; Wr=Wr0+(Wr01*dt/2); tet=tet0+(tet01*dt/2); tetr=tetr0+(tetr01*dt/2); Q=Q0+(Q01*dt/2); Q02=Arev*Q+Brev*V; Te=(P/2)*(3/2)*(Xm/(D*Wb))*((Q(1,1)*Q(5,1))–(Q(2,1)*Q(4,1))); Wr02=(P/2)*((Te–Tl)/J); Wr=Wr0+(Wr02*dt/2); W=Wr; tet02=W; tetr02=Wr; tet=tet0+(tet02*dt/2); tetr=tetr0+(tetr02*dt/2); Q=Q0+(Q02*dt/2); Q03=Arev*Q+Brev*V; Te=(P/2)*(3/2)*(Xm/(D*Wb))*((Q(1,1)*Q(5,1))–(Q(2,1)*Q(4,1))); Wr03=(P/2)*((Te–Tl)/J); Wr=Wr0+(Wr03*dt); W=Wr; tet03=W; tetr03=Wr; tet=tet0+(tet03*dt); tetr=tetr0+(tetr03*dt); Q=Q0+(Q03*dt); Q04=Arev*Q+Brev*V; Te=(P/2)*(3/2)*(Xm/(D*Wb))*((Q(1,1)*Q(5,1))–(Q(2,1)*Q(4,1))); Wr04=(P/2)*((Te–Tl)/J); Wr0=Wr0+(Wr01+2*Wr02+2*Wr03+Wr04)*(dt/6); W=Wr0; tet04=W; tetr04=Wr; tet0=tet0+(tet01+2*tet02+2*tet03+tet04)*(dt/6); tetr0=tetr0+(tetr01+2*tetr02+2*tetr03+tetr04)*(dt/6); Q0=Q0+(Q01+Q02*2+2*Q03+Q04)*(dt/6); Qqs=Q0(1,1);Qds=Q0(2,1);Q0s=Q0(3,1);Qqr=Q0(4,1);Qdr=Q0(5,1);Q0r=Q0(6,1); Te=(P/2)*(3/2)*(Xm/(D*Wb))*((Q(1,1)*Q(5,1))–(Q(2,1)*Q(4,1))); I=(1/D)*[Xrr 0 0 –Xm 0 0;0 Xrr 0 0 –Xm 0;0 0 D/Xls 0 0 0;–Xm 0 0 Xss 0 0;0 –Xm 0 0 Xss 0;0 0 0 0 0 D/Xlr]*Q; iqs=I(1,1);ids=I(2,1);ios=I(3,1);iqr=I(4,1);idr=I(5,1);ior=I(6,1); Kr=(2/3)*[cos((tet0–tetr0)) cos(((tet0–tetr0))–(2*pi/3)) cos(((tet0–tetr0))+(2*pi/3));sin((tet0–tetr0)) sin(((tet0–tetr0))–(2*pi/3)) sin(((tet0–tetr0))+(2*pi/3));.5 .5 .5]; Irotor=inv(Kr)*[iqr;idr;ior]; iar=Irotor(1,1);ibr=Irotor(2,1);icr=Irotor(3,1); Ks=(2/3)*[cos(tet0) cos((tet0)–(2*pi/3)) cos((tet0)+(2*pi/3));sin(tet0) sin((tet0)–(2*pi/3)) sin((tet0)+(2*pi/3));.5 .5 .5]; Istator=inv(Ks)*[iqs;ids;ios]; ias=Istator(1,1);ibs=Istator(2,1);ics=Istator(3,1); i=i+1; time(i)=t; Iar(i)=iar; Tee(i)=Te; Ias(i)=ias; WW(i)=(30*Wr0)/(2*pi); t=t+.0001; if t>=1.5
Tl=11.9;
end
end
|
در ادامه از دستور plot استفاده کرده و خروجی های مدنظر را ترسیم می نماییم؛
|
۱
۲
۳
۴
۵
۶
۷
۸
۹
۱۰
۱۱
۱۲
۱۳
۱۴
|
plot(time,WW);xlabel(‘t’) ;ylabel(‘Wr’)
grid on
figure
plot(time,Ias);xlabel(‘t’) ;ylabel(‘ias’)
grid on
figure
plot(time,Iar);xlabel(‘t’) ;ylabel(‘iar’)
grid on
figure
plot(time,Tee);xlabel(‘t’) ;ylabel(‘Te’)
grid on
figure
plot(WW,Tee);xlabel(‘wr’) ;ylabel(‘Te’)
grid on
|
تحلیل شبیه سازی حالت M فایل
قاعدتا انتظار ناحیه گذرا را داریم، و شاید در نگاه اول انتظار تاثیر حالت گذرا بروی جریان های استاتور که به شبکه سه فاز متعادل متصل است را نداشته باشیم، و بیشتر انتظار نوسانات شدید را بروی رتور داشته باشیم.
در برنامه ای که نوشته ایم در ابتدا از موتور خواسته ایم که به سرعت پایدار خود بدون بارداری برسد که توانسته در سرعت ۱۷۶۳٫۱ به پایداری مد نظر برسد.
همانگونه که می بینید در این حالت بدلیل استارت از حالت سکون شاهد بیشترین نوسانات در جریان استاتور، جریان رتور و گشتاتور هستیم.
از طرفی به دلیل پایین بودن توان ماشین(۳hp)؛ موتور در سرعت کمتری به گشتاور نامی رسیده است(لغزش بالاست) با دقت در نمودار گشتاور – سرعت، در سرعت ۱۰۰۰rpm موتور به گشتاور نامی خود رسیده است.
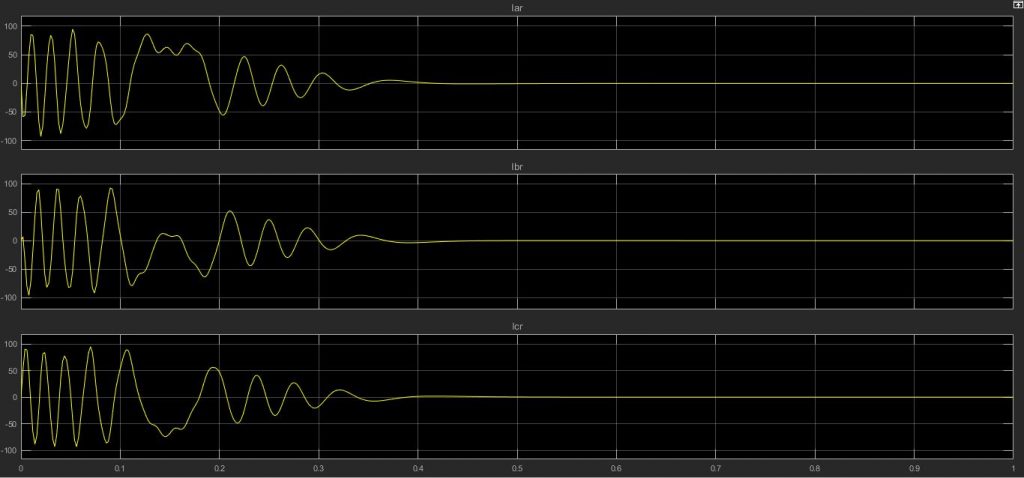
مطالب بیان شده در نمودار های زیر قابل مشاهده هستند؛
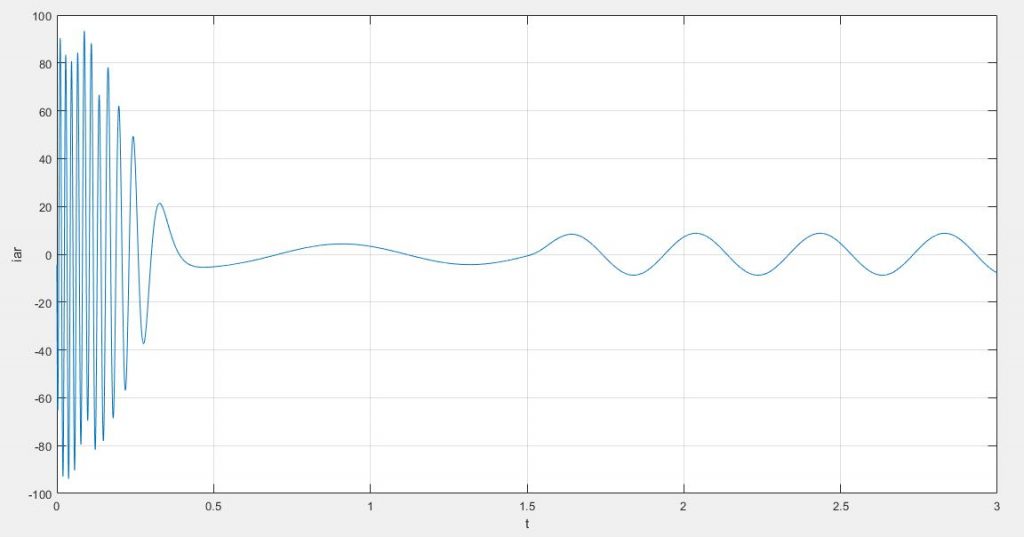
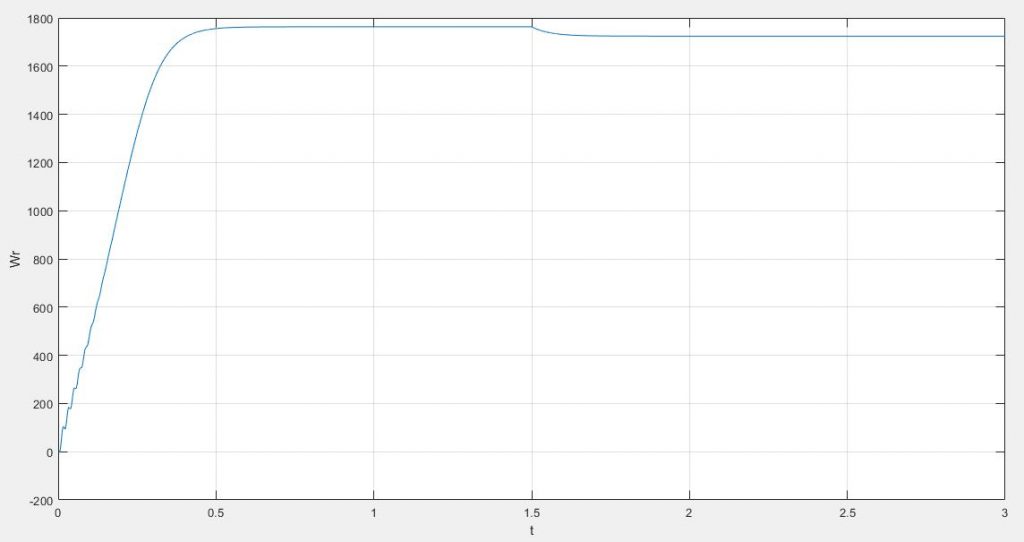
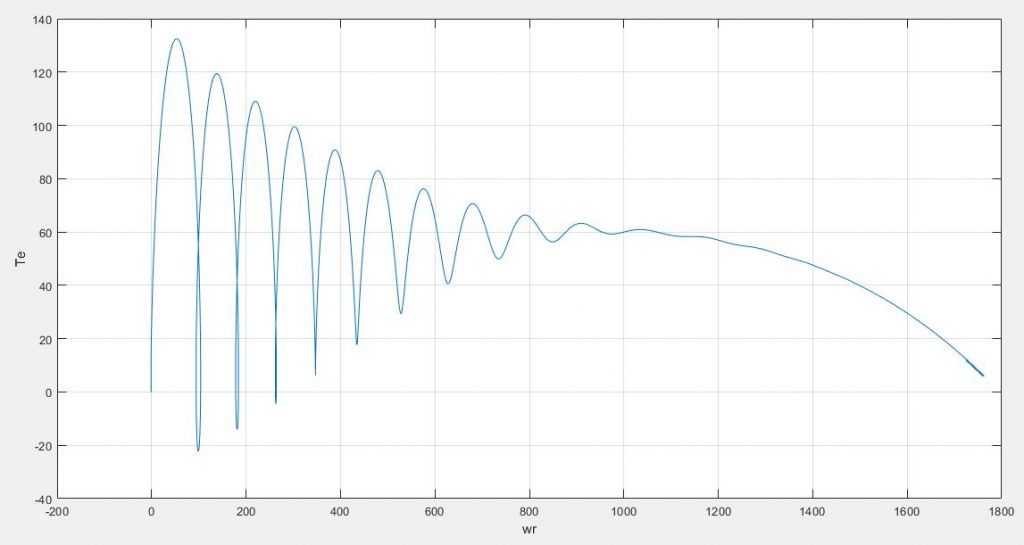
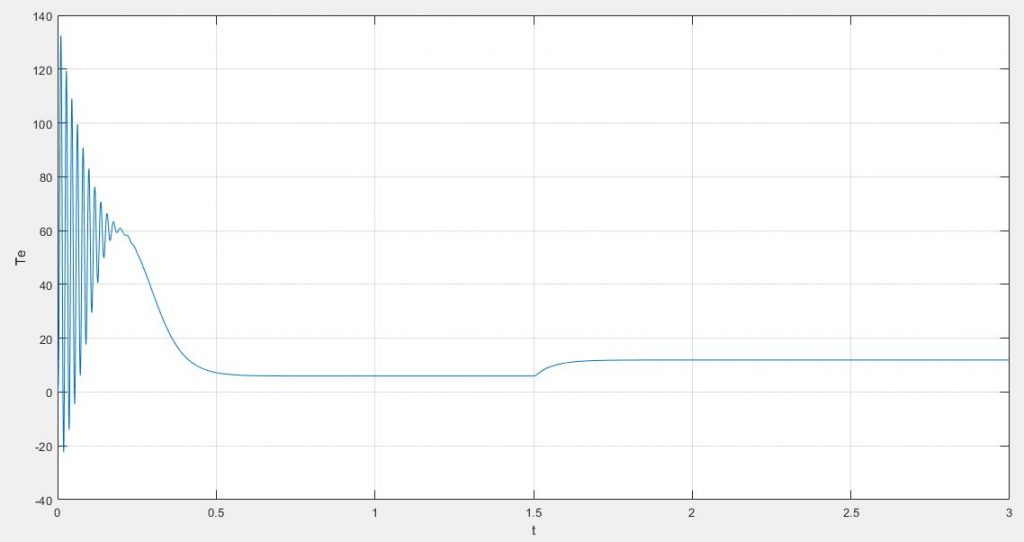
در ادامه در زمان ۱٫۵ ثانیه به موتور یک بار متصل کرده ایم که در جریان استاتور و رتور تاثیر گذاشته و عملا باعث افزایش جریان عبوری در استاتور شده است، از طرفی نیز باعث افزایش و ایجاد هارمونیک در جریان های رتور نیز گشته است
مقدمه: حسن این روش در این است که کنترل کننده موردنظر بر دانش و خواسته انسان منطبق
است بنابراین کنترل مطلوب تری خواهیم داشت.
بلوک دیاگرام سیستم ما به صورت زیر میباشد:
ورودی های کنترل کننده ما خطای سرعت و مشتق آن بمنظور ردیابی سرعت می باشد هر یک از ورودیها دارای سه تابع تعلق میباشند که به صورت زیر تعریف میشوند:
ورودی اول:خطای سرعت
ورودی دوم:مشتق خطای سرعت
خروجی:سیگنال کنترلی موتور
توابع تعلق شتاب و ولتاژ نیز مشابه سرعت میباشد.
قواعد:
میدانیم که کنترل کننده فازی بر پایه قواعد اگر- آنگاه فازی استوار است.این قواعد در این پروژه به شکل زیر زیر در نظر گرفته میشوند:
سطح قوانین بصورت زیر در می آید:
و مشاهده سطوح کنترلر بصورت زیر در می آید:
سیستم:همانطور که در بلوک دیاگرام دیده میشود سیستم ما توسط تابع تبدیل تعریف شده است که
معرف یک موتور DC میباشد.
ورودی آن سیگنال کنترلی و خروجی آن سرعت میباشد.
در این سیتم از تابع اشباع برای محدود کردن ورودی ها و خروجی ها استفاده شده است.
ورودی مرجع در این سیستم تابع پله میباشد. البته میتوانستیم از توابع دیگر نیز استفاده نماییم.
شکل موج سیگنال مرجع بصورت زیر می باشد:
شکل موج خروجی این چنین بدست می آید:
همانطور که در شکل مشخص است سرعت بر روی ۱۵۰۰rpm ثابت باقی میماند که نمایش دهنده کنترل کامل بر روی سرعت موتور می باشد و دقیقا سرعت ردیابی و یا SPEED TRACKING کامل انجام شده است.
نتایج:
- در بعضی از نقاط کاری عملکرد کنترل کننده فازی از سایر کنترل کننده ها مناسب تر است.
- با گسترش membership function ها و دامنه آنها میتوان محدوده کاری سیستم را تغییر داد.
فیلم خروجی :
شبیه سازی مدار rlc در سیمولینک :