تشخیص لبه تصاویر با الگوریتم کانتور فعال در متلب همراه مقاله (Active Countor)
تشخیص لبه تصاویر با الگوریتم کانتور فعال در متلب همراه مقاله شبیه سازی شده (Active Countor):پروژه متلب
پروژه متلب :
در این پروژه لبه یابی در واقع مجموعه عملیات ریاضی می باشد که به کمک آنها می توان نقاطی از تصویر که در آنها روشنایی بطور شدید تغییر می کند را شناسایی کرد. لبه ها معمولا بصورت خطوطی که دارای انحنا هستند مشخص می شوند.
از لبه یابی می توان برای تشخیص تغییرات شدید در روشنایی که معمولا نشانه رویدادی مهم یا تغییر در محیط است، استفاده کرد. همچنین می توان از لبه یابی در object recognition (تشخیص اشیا) و segmentation(جدا سازی عکس و تبدیل آن به چند عکس) و بینایی ماشین استفاده کرد.
برای مدل کردن لبه ها، می توان عکس ها را تابع فرض کرد.
ایده ی ابتدایی برای لبه یابی این است که همسایه هایی با تغییرات شدید را پیدا می کنیم. که برای این کار مشکلاتی وجود دارد. از جمله اینکه تا چه فاصله ای پیکسل های هماسیه را جزو همسایگی در نظر بگیریم و چگونه تغییرات را تشخیص دهیم.
پروژه متلب همانطور که گفته شد لبه ها محلی هستند که در آن تابع شدت روشنایی دچار تغییرات شدید می شود. در تصویر بالا، شکل وسط، تغییرات روشنایی عکس سمت چپ در محور افقی را نشان می دهد. شکل سمت راست مشتق اول شکل وسط را نشان می دهد. و لبه ها در واقع همان قله ها در تابع مشتق اول است.
برای اینکه مشتق اول را روی شکل پیاده سازی کنیم، از یک ماتریس (کرنل) استفاده می کنیم و آن را روی پیکسل ها حرکت می دهیم. همچنین باید یک treshold(آستانه) تعیین کنیم که بیشتر از چه مقدار تغییر در شدت روشنایی را به عنوان لبه در نظر بگیریم.
پروژه متلب گرادیان به جهتی اشاره می کند که بیشترین تغییرات شدید در روشنایی به وجود آمده. در عکس سمت چپ در محور افقی تغییرات داریم پس مشتق جزیی نسبت به x وجود دارد و مشتق جزیی نسبت به y صفر است. در عکس وسط در محور عمودی تغییرات داریم پس مشتق جزیی نسبت به y وجود دارد و مشتق جزیی نسبت به x صفر است و در عکس سمت راست در هردوجهت تغییرات داریم پس هردو مشتق جزیی وجود دارد.
برای تابع دو بعدی f(x,y) مشتق جزیی برای x به صورت بالا می باشد
برای داده های گسسته می توان از فاصله های محدود و متناهی استفاده کرد(بجای ε)(با پیکسل کار می کنیم که یک داده گسسته است. یعنی فاصله را یک در نظر می گیریم)
پروژه متلب در تصویر بالا اگر مشتق جزیی نسبت به x باشد درواقع لبه ها در محور x را بر می گرداند. شکل کرنل هم بصورت یک متریس ۱*۲ می باشد که -۱ بر روی پیکسل مورد نظر قرار می گیرد و ۱ بر روی پیکسل جلویی(پیکسل فعلی – پیکسل جلویی). اگر هم که مشتق جزیی نسبت به محور y گرفته شود لبه ها در محور y را بر می گرداند. شکل کرنل بصورت ماتریس ۲*۱ می باشد. -۱ و ۱ می تواند جا به جا شود.
اگر که از هر دو کرنل استفاده کنیم شکل بالا بدست می آید.
معمولا فیلتر ها symmetric (به این مفهوم که تعداد سطر و ستون آن برابر و فرد می باشد ) هستند. در حالی که فیلتر سمت چپ در عکس بالا اینگونه نیست. در فیلتر سمت راست که symmetric است, میزان تغییرات نسبت به پیکسل قبلی و بعدی محسابه می شود و از آن میانگین گرفته می شود.
در این حالت اثر پیکسل های همسایه هم با کمک اعداد -۱ و ۱ در نظر گرفته می شود.
در عکس بالا سمت راست، با مشخص کردن آستانه، بعضی از لبه ها که حاصل از تغییرات کمتر بودند حذف شده اند
در عکس بالا، تغییرات همواره وجود دارد ولی در لبه ها بیشتر است. بعد از مشتق گرفتن، تغییرات هم در مکان هایی که لبه هستند و هم در مکان هایی که لبه نیستند، مشخص است و به همین دلیل شناسایی لبه ها سخت تر می شود.
هنگامی که نویز یک تصویر بیشتر می شود در واقع تعداد تغییراتی که لبه نیستند هم افزایش می یابد و باعث می شود که قسمت هایی که لبه نیستند هم در تصویر نهایی نمایش داده شوند.
برای اینکه لبه یابی با دقت بیشتری انجام شود مراحل زیر انجام می شود:
- Smoothing: حذف نویز ها با کمک فیلترهایی مانند gaussian
- Threshold: چه مقداری به بعد لبه حساب شود.
- Thinning: اگر چند لبه در کنار هم و با فاصله کم وجود داشته باشد همه را یک لبه در نظر می گیریم.
- Connect edge pixles
- استفاده از فیلتر Gaussian
- محاسبه گرادیان
- non-maximum suppression: همان عملیات thinning
- اگر که یک لبه را مانند یک خط در نظر بگیریم ممکن است که میزان تغییرا در طول این خط برابر نباشد و مثلا قسمتی از این خط پررنگ تر باشد یا بخاطر آستانه تعریف شده قسمتی از خط حذف شده باشد. می توانیم از دو آستانه استفاده کنیم که مثلا اگر میزان تغییرات از آستانه بزرگتر، بیشتر باشد حتما لبه است و اگر از آستانه کوچکتر، کمتر باشد اصلا لبه نیست ولی اگر بین دو آستانه باشد، بسته به اینکه پیکسل های اطراف آن، لبه هستند یا نه خودش می تواند لبه باشد یا نباشد. مثلا در همان خطی که گفته شد اگر جایی از خط قطع شده، آن را پر می کند.
در عکس سمت راست فقط گرادیان محاسبه شده. در عکس وسط قسمت هایی که لبه نیستند حذف شده. در عکس سمت چپ لبه های نزدیک به هم به یک لبه تبدیل شده و و اگر جایی لبه ای قطع شده آن را ادامه داده.
پروژه متلب مدل کانتور فعال، که مدل مارها نیز نامیده میشود، یک چارچوب در بینایی رایانه ای است که توسط مایکل کاس، اندرو ویتکین و دمتری ترزوپولوس معرفی شده، و برای ترسیم خطوط خارجی یک شیء، از یک تصویر دو بعدی احتمالاً پر نویز تعریف شدهاست. مدل مارها در دیدگاه رایانهای محبوب است و این مدل بهطور گسترده در برنامههای کاربردی مانند ردیابی شی، تشخیص شکل، تقسیمبندی، آشکارسازی لبه و تطبیق استریو مورد استفاده قرار میگیرد.
مدل مار یک انرژی کمینه کننده و اسپلاین قابل اصلاح است که تحت تأثیر محدودیتها و نیروهای تصویر است که آن را به سمت کانتورها و نیروهای داخلی متصل میکند که مقاومت در برابر تغییر شکل را دارند. مدل مارها ممکن است به عنوان یک مورد خاص از روش کلی تطبیق یک مدل ناپایدار به یک تصویر با استفاده از به حداقل رساندن انرژی درک شوند. در دو بعد، مدل شکل فعال، یک نسخه گسسته این رویکرد را نشان میدهد، با استفاده از مدل توزیع نقطه برای محدود کردن محدوده شکل به یک دامنه صریح از یک مجموعه آموزشی یاد میشود.
مارها کل مشکل پیدا کردن خطوط در تصاویر را حل نمیکنند، زیرا این روش نیاز به دانش قبلی شکل کانتورهای طرحی شده دارد. در عوض، آنها به مکانیزمهای دیگر مانند تعامل با یک کاربر، تعامل با برخی از فرآیندهای درک تصویری سطح بالاتر یا اطلاعاتی از دادههای تصویر مجاور در زمان یا فضا بستگی دارد.
پروژه متلب در دیدگاه رایانه، مدلهای کانتور، مرزهای شکل در یک تصویر را توصیف میکنند. مدل مارها بهطور خاص طراحی شدهاند تا مشکلات را حل کنند که در آن شکل تقریبی مرز شناخته شدهاست. با داشتن یک مدل تغییر شکلپذیر، مارها میتوانند به تفاوت و نویز در تطبیق استریو و ردیابی حرکت سازگار شوند. علاوه بر این، این روش میتواند خطوط غیرواقعی در تصویر را با نادیده گرفتن اطلاعات مرزی گم شده پیدا کند.
پروژه متلب در مقایسه با تکنیکهای استخراج ویژگی کلاسیک، مدل مارها مزایای متعددی دارند:
- آنها مستقل و سازگارانه برای حداقل حالت جستجو میکنند.
- نیروهای تصویری خارجی به شیوه ای بصری بر روی مار عمل میکنند.
- ترکیب کردن Gaussian smoothing در تابع انرژی تصویر، حساسیت مقیاسی را نشان میدهد.
- آنها میتوانند برای ردیابی اجزای در حال حرکت مورد استفاده قرار گیرند.
اشکالات کلیدی روش سنتی مارهای عبارتند از:
- آنها به حالتهای مینیمم محلی حساس هستند، که با تکنیکهای انجماد شبیهسازی شده میتوانند خنثی شوند.
- ویژگیهای جزئی اغلب در طول کاهش انرژی در سراسر کانتور نادیده گرفته میشوند.
- دقت آنها بستگی به تدبیر همگرا دارد.
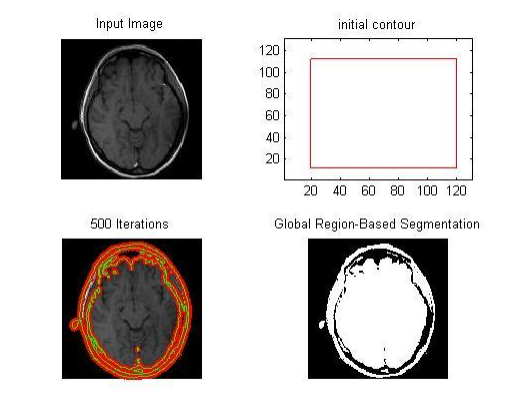
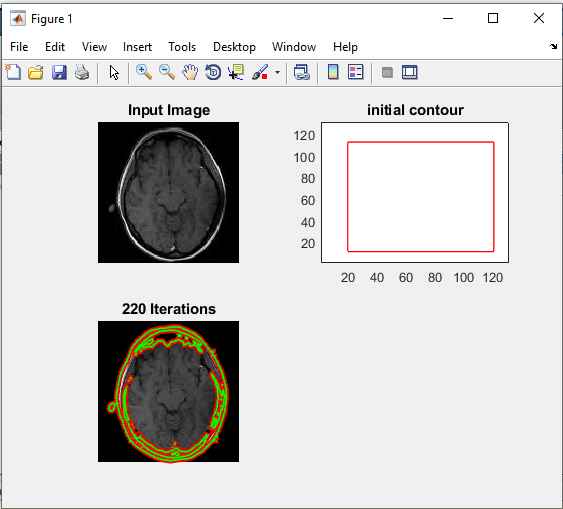
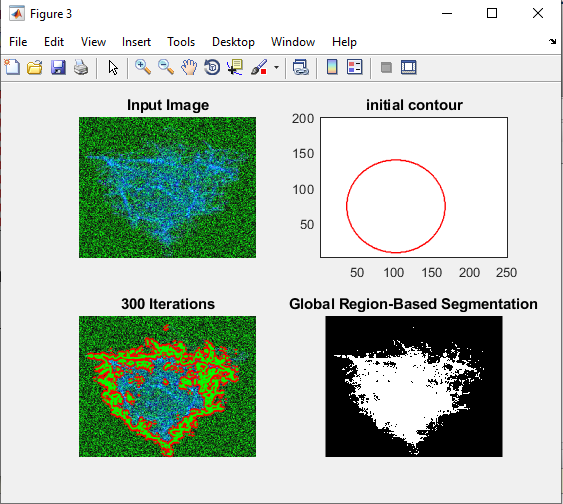
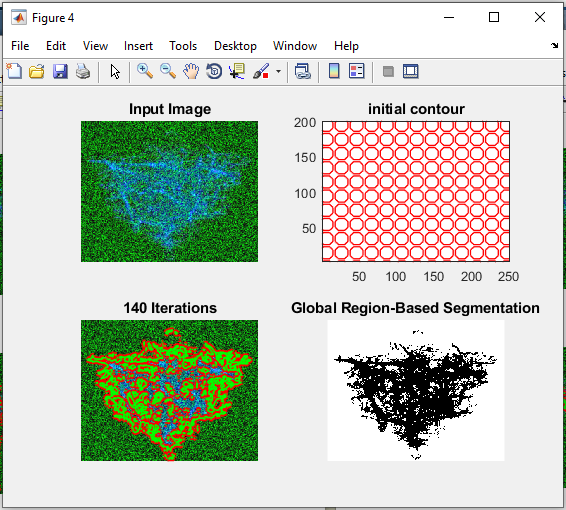
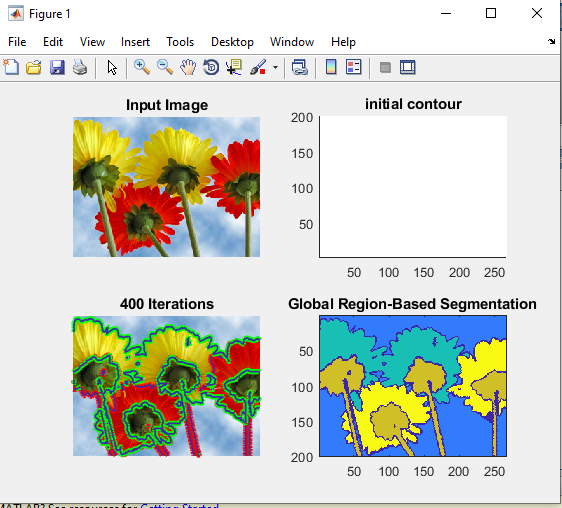
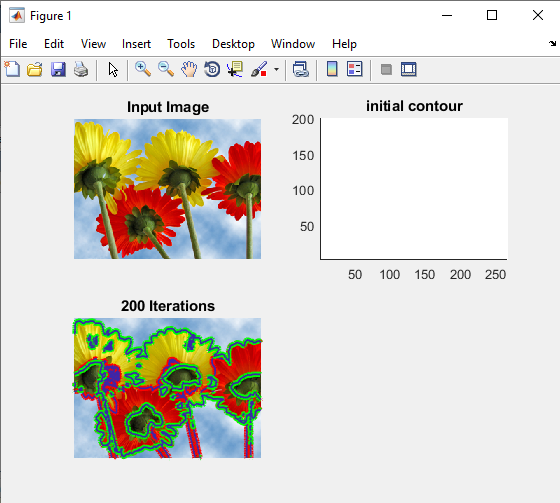
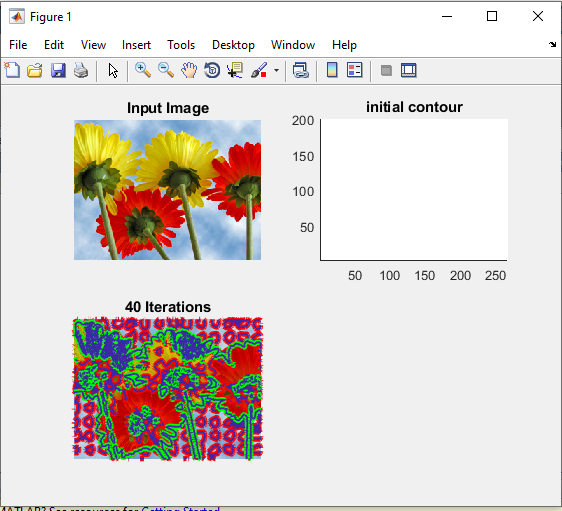
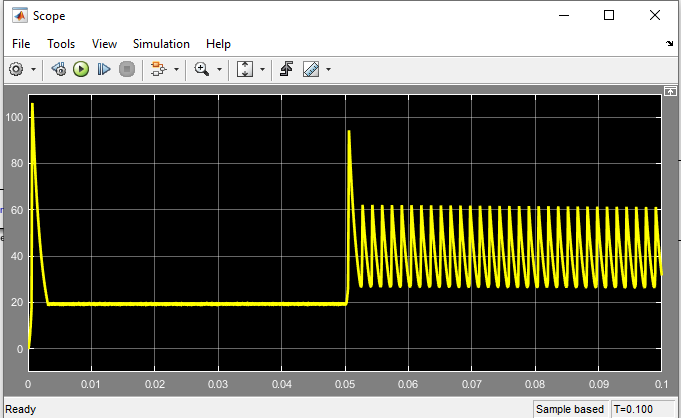
خروجی متلب :

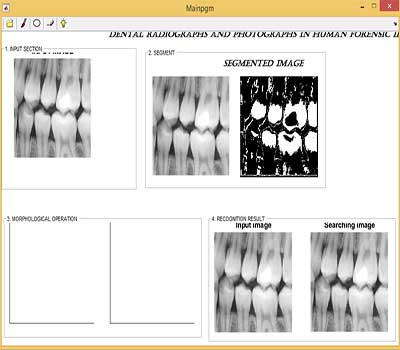

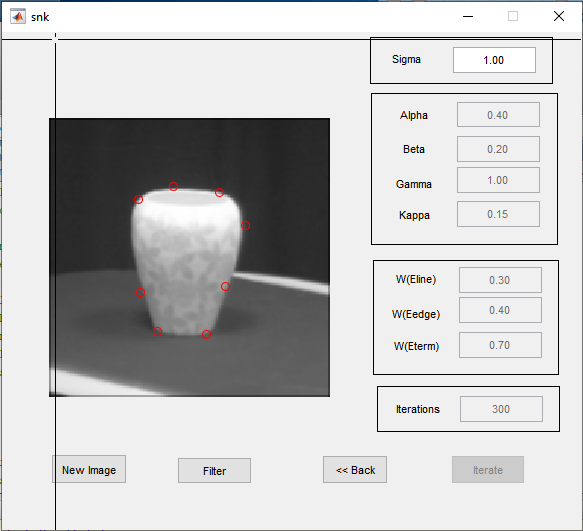
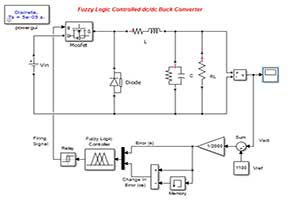
لطفاً براي ارسال دیدگاه، ابتدا وارد حساب كاربري خود بشويد