پروژه الگوریتم ژنتیک کوانتوم (QGA) با نرم افزار MATLAB:پروژه متلب ارزان
پروژه الگوریتم ژنتیک کوانتوم (QGA) با نرم افزار MATLAB:پروژه متلب ارزان
پروژه متلب ارزان: الگوریتم های ژنتیک کوانتوم برپایه دیدگاه محاسبات و کامپیوترهای کوانتومی شکل گرفته اند. مزیت این الگوریتم ها در ایجاد توازن میان تعمق و جستجو است. پژوهش های اخیر نشان می دهد این الگوریتم ها در حلّ مسائلِ بهینه سازیِ ترکیبی مانند مسئله کوله پشتی از کارایی بسیار بالایی برخوردارند. ولی در مجموع این الگوریتم ها نیز دچار مشکل گیر کردن در قلّه محلّی، و کندی سرعت همگرایی هستند. برای همین منظور بایستی روش هایی برای بهبود کارایی این الگوریتم ها پیشنهاد کرد. الگوریتم های ژنتیک کوانتوم مانند سایر الگوریتم های تکاملی یک روش جستجوی عمومی می باشند و تلفیق آنها با رو شهای جستجوی محلّی می تواند بر کارایی آنها بیفزاید. در این پژوهش می کوشیم کارایی الگوریتم های ژنتیک کوانتوم را با استفاده از روش جستجوی محلّی Simulated Annealing بهبود دهیم. نتایج نشان می دهند به کارگیری این الگوریتم موجب افزایش بسیار زیاد کارایی الگوریتم های ژنتیک کوانتوم می شود.
الگوریتم ژنتیک
پروژه متلب ارزان:بدن هر موجود زنده ای از سلول تشکیل یافته است و هر سلول هم از کروموزوم تشکیل یافته است کروموزوم ها نیز از رشته های DNA تشکیل یافته اند. به هر بلوک DNA یک ژن می گویند. و هر ژن نیز از یک پروتئین خاص و منحصر به فرد تشکیل یافته است. به مجموعهای از ژنها یک ژنم (GENOME) می گویند.
از اصطلاحاتی که از مباحث زیست شناسی به مبحث الگوریتم ژنتیک (GE) وارد شده است و باید به آتها اشاره کرد می توان به موارد زیر اشاره نمود.
- تولید مثل(crossover) که به تولید یک کروموزوم جدید توسط ترکیب ژنهای والدین می گویند.
- جهش یا تغییر ناگهانی(mutation): به تغییرات ایجاد شده در DNA میگویند
- صحت و درستی(fitness): برای یک موجود زنده به صورت موفقیت آن موجود در ایجاد حیات و تشکیل خود می گویند. البته ممکن است در نگاه اول مطالب بالا کمی نامفهوم به نظر برسد. اما در ادامه به توضیح بیشتر آنها و همچنین نوع کاربرد آنها در الگوریتم ژنتیک اشاره خواهد شد.
۱-۲-۱-کلیات الگوریتم ژنتیک
الگوریتم های ژنتیک روش قدرتمندی را برای توسعه اکتشافی مسائل بهینه سازی ترکیبی مقیاس بزرگ فراهم آورده است . انگیزه اصلی مطرح کردن الگوریتم ژنتیک می تواند این گونه عنوان شودکه «تکامل تدریجی» به شکل قابل ملاحظه ای در توسعه انواع وگونه های پیچیده از طریق مکانیزم های نسبتاً ساده تکمیلی نمود یافته است . حال سوال اساسی این است : پذیرش کدام ایده از تئوری تکامل تدریجی می تواند به ما در حل مسائل این قلمرو کمک کند ؟ این سوال با توجه به غنای پدیده تکامل تدریجی جوابهای متفاوتی دارد. هالند و دی جانگ (۱۹۷۵) از نخستین کسانی هستندکه با معرفی مفهوم الگوریتم ژنتیک به عنوان یک تکنیک جستجوی عمومی – که از تکامل تدریجی بیولوژیک در قالب بقای افراد اصلح و مبادله ساختارمند و تصادفی اطلاعات الگوبرداری می کند- درصدد پاسخگویی به این سوال برآمدند.
یک الگوریتم ژنتیک مسئله را به صورت مجموعه ای از رشته ها که شامل ذرات ریزهستند کد گذاری می کند ، سپس برای تحریک فرایند تکامل تدریجی ،تغییراتی را بر روی رشته ها ا عمال میدارد. در مقایسه با الگوریتم های جستجوی محلی ، در جستجوی عمومی که تنها یک راه حل قابل قبول وجود دارد ، الگوریتم های ژنتیک جامعه ای از افراد را در نظر میگیرند . کـــار با مجموعه ای از افراد، امکان مطالعه ساختارها و ویژگیهای اصلی افراد متفاوت را که منجر به شناسایی و کشف راه حلهای کارآمد تر می شود، فراهم میسازد . در طی مطالعه ، الگوریتم ژنتیک رشته های متناسب با ارزش را برمی گزیند و آن دسته از رشتههایی را که تنــاسب کمتری با جمعیت مورد بررسی دارند حذف میکنند .
پروژه متلب ارزان:هر کدام افراد جمیعت که تقریبهای از جواب نهایی می باشند به صورت رشته هایی از حروف یا ارغام کدگذاری می شوند این رشته ها را کروموزوم می نامند. متداول ترین حالت نمایش با ارقام صفر و یک است. حالتهای دیگر استفاده از سه رقم، اعداد حقیقی و اعداد صحیح هم مورد استفاده قرار می گیرند. برای مثال یک کروموزوم با دو متغییر a ,b با ساختار شکل ۱-۱ نمایش داده می شود.
۱۰۰۱۱۱۱۰۰۰۱۰۰۰۰۱۰۰۱۱۱
شکل ۱-۱- نمایش یک کروموزوم با ارقام صفر و یک
متغییر a با ده خانه اول سمت راست و b با یازده خانه باقیمانده نمایش داده شده است. این می تواند به علت سطح دقت و یا محدوده متغییر تصمیم گیری باشد.
مقادیرموجود بر روی کروموزومها به تنهایی معنی خاص ندارند بلکه باید از حالت کد شده خارج شوند تا به عنوان متغییرهای تصمیم گیری دارای معنی و نتیجه باشند باید توجه داشت که فرآیند جستجو بر روی اطلاعات کد شده انجام می گیرد مگر در صورتی که از ژنهایی با مقادیر حقیقی شود. بعد از اینکه کروموزومها از حالت کدگذاری شده خارج شدند می توان کارایی یا برازش هر فرد از جمیعت را محاسبه کرد. برازش مقیاس نسبی است که شایستگی افراد برای تولید نسل بعد را نشان می دهد. در طبیعت برازش معادل توانایی فرد برای بقا می باشد. تابع هدف در تعیین برازش افراد نقش تعیین کننده دارد.
در هنگام تکثیر به کمک اطلاعات اولیه ای که از تابع هدف به دست می آید. برازش هر فرد مشخص می گردد. از این مقادیر در فرآیند انتخاب استفاده می شود تا آنرا به سمت انتخاب افراد مناسب سوق دهد. هر چه برازش فرد نیبت به جمیعت بالاتر باشد احتمل بیشتری دارد که انتخاب شود. هر چه برازش نسبی آن کمتر باشد احتما انتخاب آن برای تولید نسل بعد ی کمتر می شود.
وقتی که برازش تمام افراد جمیعت مشخص شد. هر کدام با احتمالی که متناسب با میزان برازش آنهاست می توانند برای تولید نسل بعد انتخاب شوند. عمل تکثیر در الگوریتم ژنتیک برای رد و بدل اطلاعات ژنتیکی بین یک جفت یا تعداد بیشتری از افراد به کار می رود. ساده ترین نوع تکثیر تقاطع یک نقطه است دو رشته شکل را در نظر بگیرید اگر یک عدد صحیح از یک تا تعداد ارقام رشته منهای یک انتخاب شود و اطلاعات دو رشته را در دو طرف این دو نقطه عوض کنید دو رشته جدید به وجود می آیند که آنها را فرزند می نامیم به عنوان مثال اگر عدد شش را برای دو رشته شکل انتخاب کنیم نتیجه تقاطع یک نقطه ای به صورت شکل۱-۲ در می آید.
۱۱۱۰۰۱۰۰۰۱۱۱۰۱
۱۰۰۱۰۱۱۰۱۰۱۱۰۱
شکل ۱-۲-a دو کرموزوم قبل از تقاطع (والدین)
۱۱۱۰۰۱۱۰۱۰۱۱۰۱
۱۰۰۱۰۱۰۰۰۱۱۱۰۱
شکل ۱-۲-b دو کروموزوم بعد از تقاطع (فرزندان)
این عملگر الزاما بر تمامی رشته های یک جمیعت اعمل نمی شود بلکه برای اعمال آن بر یک جفت رشته یک احتمال نسبت داده می شود. بعد از این مرحله با احتمال جدید عملگر جهش بر روی رشته های تولید شده اعمال می گردد. در جهش ، هر فرد به تنهایی با توجه به قوانیین احتما می تواند تغییر کند.
در نمایش دودویی رشته ها، جهش به معنای تغییر مقدار یکی از خانه های رشته از صفر به یک و یا از یک به صفر می باشد. به عنوان مثال جهش در هفتمین خانه اولین فرزند تولید شده در مثال قبل منجر به ایجاد رشته شکل ۱-۳ می گردد.
۱۱۱۰۰۱۰۱۱۰۱۱۰۱ ۱۱۱۰۰۱۰۰۱۱۰۱۱۰۱
شکل ۱-۳ کروموزوم بعد از جهش
پروژه متلب ارزان:به جز دوعملگر تقاطع و جهش که در تمام الگوریتمهای ژنتیک کاربرد دارند عملگرهای دیگر هم هستند که در مسائل خاص استفاده می شوند. از آن جمله می توان عملگر جمع یا عملگر حذف و همچنین عملگر جابجایی را نام برد.
بعد از مراحل تکثیر و جهش کروموزوم ها از حالت کدشده خارج می شوند و مقدار تابع هدف هریک محاسبه می شود سپس به هرکدام برازشی اختصاص داده می شود. حال اگر لازم باشد دوباره مراحل انتخاب و تکثیر و غیره انجام می گیرد. در طول این فرایند انتظار می رود که کارایی متوسط جمعیت جواب ها افزایش یابد. الگوریتم وقتی پایان می یابد که هدف خاصی برآورده شود. به عنوان مثال تعداد مشخصی نسل ایجاد شده باشد، انحراف میانگین کارایی افراد به مقدار مشخصی برسد و یا به یک نقطه خاص در فضای جستجو برسیم.
۱-۲-۲-قسمت های مهم الگوریتم ژنتیک
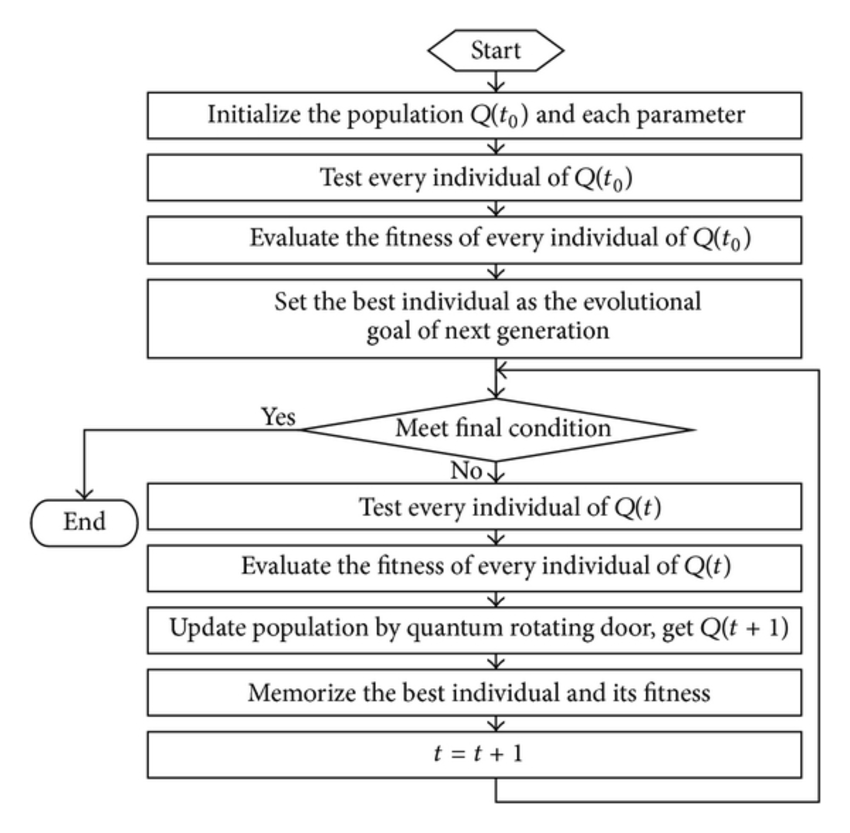
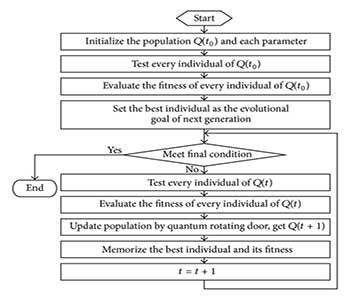
الگوریتم ژنتیک ساده توسط گولبرگ شرح داده شده و در این قسمت برای توضیح قسمت های اصلی ارائه می شود. کد برنامه مجازی در شکل نشان داده شده است که نکات مهم الگوریتم ژنتیک ساده را در بردارد. جمعیت در زمان t با متغیر وابسته به زمان P(t) نشان داده شده است. به کمک این برنامه اجزای مهم الگوریتم ژنتیک شرح داده می شود. این برنامه در زیر نشان داده شده است:
{
Generate initial population Pt
Evaluate population Pt
while stopping criteria not satisfied
repeat
{
Select elements from Pt to put
into Pt+l
Crossover elements of Pt and put
into Pt+l
Mutate elements of Pt and put
into Pt+l
Evaluate new population Pt+l
Pt = Pt+l
}
}
پروژه متلب ارزان:الگوریتم ژنتیک بر روی مجموعه ای از جواب ها که جمعیت نامیده می شوند اعمال می گردد. افراد یک جمعیت رشته هایی از اعداد هستند که کروموزوم نامیده می شوند و حاوی اطلاعات کد شده پارامترهای تصمیم گیری اند. به صورت معمول جمعیت شامل ۳۰ تا ۱۰۰ فرد است. اگرچه تاحدود ۱۰ فرد هم به کار می رود.
معمولی ترین شیوه نمایش کروموزوم ها در الگوریتم ژنتیک به شکل رشته های دودویی است. هر متغیر تصمیم گیری به صورت دودویی در آمده و سپس با کنار هم قرار دادن این متغیرها کروموزوم ایجاد می شود. اگرچه این روش گسترده ترین شیوه کدگذاری است اما شیوه های دیگری مثل نمایش اعداد حقیقی در حال گسترش است. در فضای بعضی از مسائل این بحث پیش آمده که نمایش دودویی طبیعت جستجو را پیچیده می کند و علاوه بر آن مشکلات دیگری هم دارد. به عنوان مثال دو عدد کدشده ۱۰۰۰۰۰۰۰ و ۰۱۱۱۱۱۱۱ را در نظر بگیرید.مقادیر حقیقی این دو عدد فقط یک واحد با هم اختلاف دارند. ولی مقادیر کد شده از لحاظ ظاهری اختلاف زیادی با هم دارند. این اختلاف در هنگام اعمال عملگرهای معمول ژنتیک، مشکل زا می شود. به بیان دیگر یک تغییر کوچک در فضای کدشده مشابه آن تغییر در فضای کدنشده را ایجاد نمی کند.
نمایش ژن ها با اعداد حقیقی برای به دست آوردن امتیازاتی در بهینه سازی توابع عددی مطرح شد. این شیوه نمایش به علت اینکه نیازی به خارج شدن از حالت کدشده ندارد و به حافظه کمتری نیاز دارد مورد استفاده قرار می گیرد. در این شیوه چون تبدیل به حالت دودویی نداریم از دقت مقادیر به علت این تبدیل کاسته نمی شود. کدگذاری با اعداد حقیقی برای بهینه سازی توابع بهترین نتایج را می دهد.
نکته مهمی که در هنگام کدگذاری باید به آن دقت شود طبیعت مسأله و قیود آن است. بعد از این اعمال عملگرهای ژنتیک به کروموزوم ها، جواب های جدیدی به دست می آید که ممکن است در قیدهای مسأله صادق نباشند. این حالت در بسیاری از مسائل دارای قید به وقوع می پیوندد. ساده ترین راه حل استفاده از تابع جریمه در تابع هدف است. با این شیوه برازش جواب های خارج از قیود به شدت کم می شود. در نتیجه فرآیند انتخاب به سمت کروموزوم هایی که در قیدها صادقندگرایش پیدا می کند. هرچه میزان جریمه بیشتر باشد الگوریتم با سرعت بیشتری همگرا می شود و در ضمن احتمال رسیدن به بهینه موضعی افزایش می یابد. به همین دلیل میزان جریمه را در مسائل مختلف به وسیله سعی و خطا مشخص می کنند و این مورد اشکالی است که از تابع جریمه گرفته می شود. با توجه به مطالب بین شده نکات مهم در الگوریتم های ژنتیک به شرح زیر است:
۱- شرایط جمعیت اولیه میتواند در سرعت رسیدن به جواب بسیار تأثیرگذار باشد. یعنی اگر جمعیت اولیه مناسبتر باشد، بسیار سریعتر به جواب میرسیم. بنابراین گاهی در بعضی از مسئلهها به جای آن که جمعیت اولیه به صورت تصادفی ایجاد شود، از اعمال شرایط خاص مسئله به جمعیت اولیه نیز استفاده میشود.
۲- با توجه به وجود پارامترهای تصادفی در الگوریتم مسئله حتی در صورت استفاده از جمعیت اولیه یکسان ممکن است در اجراهای مختلف الزاماً جوابهای یکسان به دست نیاید و البته در صورت استفاده از جمعیت اولیه متناوت این پدیده ملموستر خواهد بود.
۳- تابع ارزش در اینگونه از الگوریتمها از اهمیت بسزایی برخوردار است؛ چرا که معمولاً در اکثر مسائل در اثر ترکیب، حالتهایی رخ میدهد که منطبق بر شرایط مسئله نیست و حتی فاقد معنی و مفهوم است. بنابراین تابع ارزش باید به گونهای طراحی شود که به ازای این حالات مقادیر بسیار کمی برگرداند و از طرفی باید برای نزدیک شدن به هدف بسیار خوب تخمین بزند.
۴- یکی از پدیدههای جالب این است که ممکن است در نسلهای میانی نمونههایی بروز کنند که از نظر تابع ارزش و خوب بودن بسیار مناسب باشند. یک روش این است که اینگونه موارد را شناسایی کنیم و در نسل بعدی نیز از آنها استفاده کنیم. به این تکنیک نخبهگرایی میگویند که عملاً تأثیر بسزایی در رسیدن به جواب مسئله دارد.
۱-۲-۲-۱-تابع هدف و تابع برازش
تابع هدف شاخصی از نحوه عملکرد افراد در فضای مسأله به ما می دهد. به عنوان مثال در مسأله ای که هدف مینیمم سازی باشد مناسب ترین فرد آن است که تابع هدفش کمترین مقدار را داشته باشد. این اطلاعات خام معمولاً به عنوان یک مرحله میانی در تعیین کارایی نسبی افراد در الگوریتم ژنتیک بکار می روند. تابع بعدی در این مرحله تابع برازش است. این تابع برای تبدیل مقادیر تابع هدف به مقیاسی برای سازگاری و کارایی نسبی افراد بکار می رود. مقادیر برازش را مثبت در نظر می گیرند. بنابراین در مواردی که مقدار تابع هدف منفی می شود یکی از کارهای تابع برازش مثبت کردن این مقادیر است.
در بعضی از موارد مقدار تابع برازش متناسب با تعداد فرزندانی است که انتظار می رود از آن کروموزوم تولید شود. یک روش معمول این است که برازش هر فرد برابر حاصل قسمت تابع هدف بر مجموع توابع هدف در نظر گرفته شود. این روش در مواقعی که توابع هدف منفی هستند با مشکل مواجه می گردد. از یک تبدیل خطی و مثبت سازی برای غلبه بر این مشکل استفاده می شود.
استفاده از تبدیل خطی ممکن است باعث ایجاد همگرایی زودرس شود. الگوریتم انتخاب کروموزوم ها را بر پایه برازش آن ها انتخاب می کند. استفاده از تبدیل خطی باعث می شود که تعداد فرزندانی که از هر کروموزوم انتظار می رود متناسب با کارایی آن باشد. اگر هیچ قیدی در نظر گرفته نشود آنگاه کروموزوم هایی که کارایی بالا دارند بر دیگر کروموزوم ها چیره شده و نسل جدید را فرزندان آن ها تشکیل می دهند. با این عمل احتمال این که به نقاط بهینه نسبی و نه بهینه کلی برسیم زیاد می شود. به صورت مشابه اگر پراکندگی جمعیت کم باشد با تبدیل خطی زمان لازم برای رسیدن به بهینه کلی زیاد خواهد شد.
با محدود کردن میزان تکثیر کروموزوم ها هیچ کروموزومی نمی تواند بیش از حد فرزند ایجاد کند. این کار مانع همگرایی زودرس می شود. می توان برازش افراد را متناسب با جایگاه آن ها در جمعیت و نه مقادیر تابع هدف آن ها انتخاب کرد. متغیری به نام sp (0 < sp < 1) برای تعیین تمایل انتخاب بهترین فرد معین شده و برازش دیگر افراد بوسیله رابطه (۱-۱) مشخص می شود.
(۱-۱)
F مقدار برازش، N تعداد افراد و x فرد دارای مرتبه i در جمعیت است. در بهترین فرد i = 1 و در بدترین فرد i = N است. برای مثال اگر جمعیت ۴۰ عضو داشته باشد و sp = 0.9 باشد آنگاه برازش افراد در محدوده [۰٫۹ ۱٫۱] قرار می گیرد. ضعیف ترین کروموزوم برازش ۹/۰ و بهترین کروموزوم برازش ۱/۱ را دارا خواهد بود فاصله بین مقادیر برازش دو کروموزوم مجاور ۰۰۵/۰ می شود.
روش دیگری نیز برای تعیین برازش افراد بر حسب جایگاه آن ها در جمعیت وجود دارد. در این شیوه برازش از فرمول زیر محاسبه می شود:
(۱-۲)
در این روش فاصله بین مقادیر برازش ها یکسان نیست ولی مجموع مقادیر برازش یک می شود.
۱-۲-۲-۲- انتخاب
انتخاب فرایند تعیین دفعاتی است که یک فرد خاص می تواند در مرحله تکثیر شرکت کند. به بیان دیگر تعداد فرزندانی که از یک فرد بوجود خواهند آمد، در این مرحله مشخص می شوند. انتخاب افراد به طور کلی شامل دو فرایند جداگانه است.
مشخص کردن تعداد دفعاتی که انتظار می رود یک فرد در مرحله تکثیر شرکت کند.
تبدیل اعداد بدست آمده از مرحله قبل به اعداد صحیح.
مرحله اول مربوط به تبدیل برازش افراد به احتمال شرکت افراد در مرحله تکثیر است و بیشتر در مرحله تعیین برازش انجام می شود. مرحله دوم انتخاب احتمالی افراد است که بر اساس برازش نسبی صورت می گیرد و نمونه برداری هم خوانده می شود.
بسیاری از تکنیک های انتخاب از چرخ گردان استفاده می کنند. یک فاصله از صفر تا مجموع برازش ها در نظر گرفته می شود. سپس مقادیر برازش آنها در کنار هم روی این فاصله قرار می گیرند. سایز فاصله مربوط به هر فرد متناسب با برازش آن است. به جای خط راست از یک دایره هم می توان استفاده کرد.
محیط دایره برابر مجموع برازش های کلیه افراد جمعیت است. برای انتخاب یک فرد عددی بین یک و صفر تا مجموع برازش ها انتخاب شده و فردی که این نقطه در محدوده آن قرار می گیرد انتخاب می شود. این فرایند تا انتخاب تعداد افراد لازم تکرار می گردد.
روش انتخاب با چرخ گردان یک نمونه برداری تصادفی با جایگزینی محسوب می شود. اندازه هر قسمت و احتمال انتخاب هر فرد در طی فرایند انتخاب ثابت باقی می ماند. هر فرد که احتمال انتخاب آن صفر نباشد از لحاظ تئوری می تواند والد تمامی نسل بعد باشد.
می توان اندازه هر بخش را بعد از انتخاب شدن تغییر داد. هربار که یک فرد انتخاب شد اندازه بخش مربوط به آن یک واحد کم می شود. اگر اندازه بخش منفی شود آنگاه صفر در نظر گرفته می شود.
از چرخ گردان در یک روش دیگر هم استفاده می شود. در این روش به مقدار جز صحیح برازش هر فرد یک کپی از آن انتخاب می شود. سپس مقادیر اعشاری برازش ها در یک چرخ گردان قرار گرفته و باقی مانده انتخاب ها به یکی از دو روش قبلی با جایگذاری و یا بدون آن مشخص می شوند.
روش دیگر نمونه برداری تصادفی کلی است. در این روش به جای انتخاب یک فرد در هر مرحله تمامی افراد لازم را با هم انتخاب می کنیم. اگر N انتخاب لازم باشد عددی مثل P را در فاصله صفر تا حاصل تقسیم مجموع برازش ها بر N به صورت تصادفی انتخاب کرده سپس افراد را با یک ترتیب تصادفی می چینیم. حال N نشانگر را در موقعیت های P و P + 1 و… P + N -1 قرار می دهیم.
هر فردی که نشانگر بر روی آن قرار گیرد انتخاب می شود. در این شیوه زمان کمتری برای انتخاب صرف می شود.
در بعضی مقالات از انتخاب مسابقه ای استفاده شده است. در این روش هر بار تعداد دو و یا چند کروموزوم بوسیله چرخ گردان انتخاب شده است و از میان آن ها بهترینشان انتخاب می شود و این کار تا انتخاب تمام افراد لازم ادامه می یابد.
روشی برای اعمال قید بدون اعمال تابع جریمه پیشنهاد شده که در مرحله انتخاب انجام می شود. هربار دو فرد بوسیله چرخ گردان انتخاب می شوند و بین آن ها مقایسه صورت می گیرد. اگر هر دو مجاز بودند آنکه برازش بالاتری دارد انتخاب می شود. اگر هر دو غیر مجاز بودند آنکه انحراف از قید کمتری دارد انتخاب می شود. در صورتی که یکی مجاز و دیگری غیر مجاز باشد آنکه مجاز است انتخاب می شود. در این شیوه دیگر نیاز به تابع جریمه نیست و مستقل از نوع مسأله است.
در تمام روش های بالا نظم بین افراد ایجاد شده باید قبل از رفتن به مرحله بعد و اعمال عملگرها بر هم زده شود.
۱-۲-۲-۳- تقاطع
عملگر اساسی در الگوریتم ژنتیک برای تولید کروموزوم عملگر جابجایی می باشد. همانند آنچه در طبیعت وجود دارد، عملگر جابجایی افراد جدیدی تولید می کند که از قسمت های مختلف ژن والدین خود تشکیل شده اند. این عملگر بر روی یک جفت از کروموزوم های انتخاب شده اعمال می شود. این عملگر، مهم ترین عملگر ژنتیکی بوده و به عنوان موتور جستجوی الگوریتم ژنتیک در فضای کاوش می باشد که عملکرد الگوریتم ژنتیک به مقدار وسیعی به نوع عملگر جابجائی به کار رفته در آن بستگی دارد. انجام عمل جابجائی به روش کدگذاری جوابها بستگی دارد. عملگر اصلی ایجاد نسل جدید در مرحله تکثیر تقاطع است. همانند کروموزوم ها در طبیعت فرزندان حاصل از این عمل هریک بخشی از اطلاعات روی کروموزوم های والدین را دارند. ساده ترین نوع تقاطع، تقاطع یک نقطه ای است. در زیر چند نمونه روش جابجائی برای دو حالت کدگذاری دودوئی و حقیقی ارائه شده است.
روش های معمول جابجائی دودویی شامل جابجایی تک نقطه، دو نقطه، چند نقطه و جابجایی یکنواخت می باشد. ساده ترین حالت جابجا کردن، جابجایی تک نقطه ای (Single Point) است. در جابجایی تک نقطه ای، ابتدا جفت کروموزوم والد (رشته دودویی) در نقطه مناسبی در طول رشته بریده شده و سپس قسمت های بعد از نقطه برش، با هم عوض می شوند. بدین ترتیب دو کروموزوم جدید به دست می آید که هرکدام از آن ها ژن هایی را از کروموزوم های والد به ارث می برند.
برای جابجایی چندنقطه ای m موقعیت جابجا شدن، ، که نقطه جابجایی و l طول کروموزوم می باشد، را به صورت تصادفی و بدون تکرار انتخاب می کنیم. سپس جهت ایجاد فرزندی جدید بیت های بین نقاط مشخص شده در والدین با هم عوض می شوند.
به هر بیت از رشته کروموزوم ها یک آلل (Allele) گفته می شود. بخش بین اولین آلل تا اولین نقطه قطع، بین والدین جابجا نمی شود. این عملیات در شکل نشان داده شده است. فلسفه انجام جابجایی در چند نقطه و البته حالت های مختلف دیگر عملگر جابجایی این است که، قسمت هایی از کروموزوم که بیان کننده سهم به سزائی در عملکرد بهتر یک عضو خاص هستند ممکن است در زیر رشته های همسایه یافت نشوند.
به نظر می رسد نحوه عملکرد عملگر جابجایی در چند نقطه (Multipoint Crossover) نسبت به روش همگرایی به مقادیر بالاتر برازندگی به پیشرفت و توسعه جستجو در فضای داده های مربوطه بیشتر کمک می کند، لذا جستجو در دامنه جواب قوی تر می شود.
یانگ عملگر جابجایی چند نقطه را مورد بررسی قرار داده و ثابت کرد که عملگر جابجایی دو نقطه بهتر از تک نقطه بوده و همچنین اضافه کردن نقاط جابجایی بیشتر، عملکرد الگوریتم ژنتیک را کاهش می دهد.
عملگرهای جابجایی یک نقطه ای و چندنقطه ای در جایی اثر می کنند که کروموزوم دقیقاً در آن نقاط فقط می تواند جدا شود، اما عملگر جابجایی یکنواخت پتانسیل جابجاشوندگی را به تمام نقاط یک کروموزوم به صورت یکنواخت نسبت می دهد. به این معنی که احتمال جابجا شدن کروموزوم در هر نقطه برابر خواهد بود. یک الگوی بیان کننده عمل جابجایی (به همان طولی که کروموزوم ها دارند) به صورت تصادفی ایجاد می شود و مقدار تعیین شده در هر بیت از این نمونه نشان می دهد که کدام یک از والدین به عنوان مرجع مقداردهی برای آن بیت از فرزند خواهد بود. تعداد نقاط برش ثابت نیست ولی به طور متوسط برابر است.
دو کروموزوم اولیه (والدین) و الگوی عملگر جابجایی و فرزندان حاصل را در نظر بگیرید.
در اینجا مشاهده می شود که فرزند اول بدین صورت ایجاد شده است که اگر بیت مربوط در الگوی جابجایی (mask) 1 باشد مقدار آن بیت در برابر با مقدار بیت متناظر در و همچنین اگر بیت مربوط در الگوی جابجایی ۰ باشد مقدار آن بیت در برابر با مقدار بیت متناظر در است.
رشته با جابجا کردن و و در نظر گرفتن همین شیوه ایجاد شده است یعنی مقدار ۱ در رشته mask به معنی مقدار بیت متناظر در برای همان بیت در است.
مشخصاً عملگر جابجایی یکنواخت همانند عملگر جابجایی چند نقطه ای باعش کاهش خطای همگرایی، ناشی از طول باینری استفاده شده و نوع کد کردن سری پارامترهای داده شده، می شود. این مسأله کمک می کند گه بر خطای همگرایی موجود در حالت جابجایی تک نقطه ای در زیررشته های کوتاه غلبه کنیم بدون آنکه نیاز به دانستن مقادیر بیت های اعضا در کروموزوم های ارائه شده داشته باشیم.
Spears و Dejong نشان داده اند که چگونه جابجایی یکنواخت به وسیله احتمال عوض شدن و جابجا شدن بیت ها پارامتری می شود. این پارامتر فوق العاده می تواند بدون توصیف یک همگرایی مربوط به طول رشته های استفاده شده، در کنترل مقدار تغییریافته در طول ترکیب بندی مجدد استفاده شود، هنگامی که از عملگر جابجایی یکنواخت در مقادیر حقیقی استفاده می شود به آن ترکیب بندی منفصل گفته می شود.
در مقایسه هایی که بین عملگرهای دودویی به هر دو صورت تئوری و تجربی انجام شده و نتایج به دست آمده نشان می دهد که، هیچ یک از این عملگرها نمی تواند به طور مطلق بهترین بوده و اختلاف در سرعت این روش ها هم نمی تواند بیش از %۲ باشد.
عملگر جابجایی دیگری که مطرح می شود به اسم Shuffle است. یک نقطه قطع مجزا انتخاب می شود اما قبل از اینکه بیت ها تعویض شوند، در هر دو والد بیت ها به صورت تصادفی جابجا می شوند. بعد از ترکیب بندی مجدد بیت ها در رشته فرزند جایگذاری می شوند. این عملگر نیز خطای همگرایی رشته ها را با جابجایی تصادفی بیت ها در هر جایی که عملگر جابجایی انجام می شود حذف می کند.
عکس خروجی برنامه
پروژه متلب ارزان:
http://www.porojeamadematlab.ir
تنها وبسایت پروژه متلب ارزان
پروژه متلب ارزان
الگوریتم ژنتیک، متلب،پروژه آماده،پایان نامه آماده، ژنتیک، الگوریتم کرم شب تاب، مسائل بهینه سازی، متلب،پروژه آماده،پایان نامه آماده،پروژه متلب ارزان



لطفاً براي ارسال دیدگاه، ابتدا وارد حساب كاربري خود بشويد