طراحی الگوریتم پردازش تصویر برای ردیابی اشیاء متحرک قسمت دوم:پروژه متلب برق  - انجام پروژه متلب |پروژه متلب | انجام پروژه متلب برق | شبیه سازی با متلب

طراحی الگوریتم پردازش تصویر برای ردیابی اشیاء متحرک قسمت دوم:پروژه متلب برق 

طراحی الگوریتم پردازش تصویر برای ردیابی اشیاء متحرک قسمت دوم :پروژه متلب برق

روش پیشنهادی

٣-١) مقدمه

پروژه متلب برق : تخمین حرکت ، یک قسمت مهم از هر سیستم پردازش ویدیویی میباشد در این فصل ، تمرکز روی تخمین حرکت دو بعدی است . تخمین حرکـت دو بعـدی عـلاوه بـر اینکـه دامنـۀ وسـیعی از کاربردها شامل تغییر نرخ نمونه برداری١٠، فیلترکردن ، فشرده سـازی ویـدیوئی١١ و غیـره را شـامل میشود، اغلب یک مرحله پیش پـردازش لازم درتخمـین حرکـت سـه بعـدی و همچنـین تخمـین ساختار سهُ بعدی نیز محسوب میشود. بسته به نوع کاربرد، روشهای تخمین حرکت میتوانند بسیار متنوع باشند.برای مثال ، برای کاربردهای بینایی ماشین کـه بردارهـای حرکـت دوُ بعـدی بـرای اسـتخراج ساختار و پارامترهای حرکت سـه بعـدی اسـتفاده مـیشـوند، یـک مجموعـۀ محـدود و پراکنـده از بردارهای حرکت دوبعدی در نقاط مشخصۀ خاص کفایت می کند.

از طرف دیگر، برای کاربردهای فشرده سازی ویدیوئی، بردارهـای حرکـت تخمـین زده شـده ، برای پیش گویی حرکت در یک فریم که باید براساس یک فریم مرجع کـد شـده قبلـی، کـد شـود استفاده      میشوند. هدف نهایی، مینـیمم کـردن تعـداد بیتهـای اسـتفاده شـده بـرای کـدکردن بردارهای حرکت و پیش بینی خطاها میباشد. یک چالش ١٢ بین دقت حرکت تخمـین زده شـده و تعداد بیتهای استفاده شده برای مشخص کردن مشخصات حرکت وجود دارد [١].

پروژه متلب برق :ممکن است حتی هنگامی که حرکت تخمین زده شده یک بیان دقیق از یک حرکـت واقعـی فیزیکی نمیباشد، منجر به پیش بینی مطلوبی از حرکت شود لذا همچنان یـک تخمـین خـوب در نظر گرفته میشود. این فصل ، بر روی انواع الگوریتمهای تخمین حرکت دو بعدی که برای پـردازش حرکت اعم از پیش بینی ، فیلتر کردن و پـالایش ، درون یـابی حرکـت ١٣ و غیـره شـکل گرفتـه انـد متمرکز میشود [٢ ،٣ ۴].

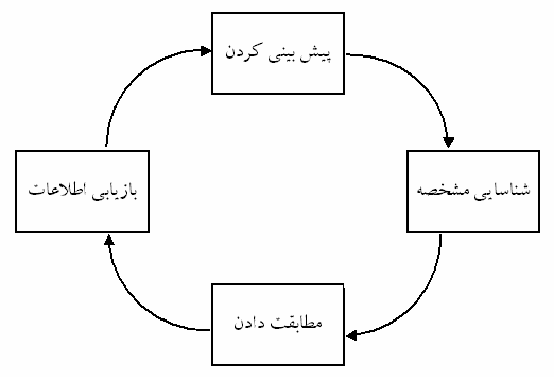
بلوک دیاگرام یک سامانه ردیاب در شکل ٣-١ نشان داده شده  که در ادامـه ابتـدا روشـهای تشخیص شئ متحرک گفته شده و نیز تعدادی از این روش هـا بـا هـم مقایـسه مـی شـود سـپس روشهای مختلف تخمین بر پایه شار نوری گفته شده ودر انتها با هم مقایسه می شوند.

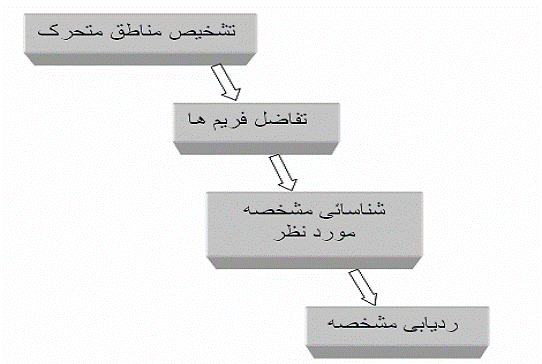
٣-١ بلوک دیاگرام مربوط به یک سامانه ردیاب

-٢ تشخیص مناطق متحرک

در این قسمت به تشریح چگونگی تشخیص اشیاء متحرک می پردازیم ،برای تشخیص منـاطق

متحرک و اشیاء متحرک دو روش را تشریح می نمائیم :

٣-٢-١ روش تفاضل دو تصویر متوالی

پروژه متلب برق :در این روش برای استخراج نواحی حرکت ، از اختلاف دو یا سه قاب متوالی در دنباله تصاویر استفاده می کنند. پس از این عمل ، تصویر حاصل از تفاضل قاب ها را با استفاده از یک تابع ، آستانه ای می – کنند. این روش بسیار سریع و برای محیط های پویا بسیار مناسب است . اما مشکل ایـن روش ایـن است که برخی از نواحی حرکت را ممکن است حذف نماید و یا برخی از نواحی ثابت اطـراف جـسم متحرک را به عنوان ناحیه حرکت در نظر بگیرد. در [۵١] از تفریق زمانی برای بدست آوردن ناحیه

حرکت استفاده کرده اند. آنها قدرمطلق تفاضل دو قاب متوالی را به صورت زیر بدست آورده اند:

سپس با استفاده از آلگوریتم برچسب زنی اجزاء پیوسته نواحی حرکـت را اسـتخراج کـرده انـد. در نسخه اصلاح شده تفریق زمانی از اختلاف سه قاب متوالی استفاده مـی شـود. روش تفریـق زمـانی اگرچه بسیار سریع است ولی به تنهایی از کارایی بالایی برخوردار نیست و نواحی حرکت را به طـور کامل تشخیص نمی دهد. ترکیب این روش با روش های دیگر می تواند نتایج بهتری به دست دهد.

٣-٢-٢  روش حذف پس زمینه

در این قسمت روش هایی که سعی در مدل کردن پس زمینه در طول زمان را دارند را بررسـی مـی- کنیم . در اینگونه از روش ها یک اطلاعات آماری از هر یـک از پیکـسل هـای تـصویر در طـول زمـان بدست میآید و در زمانی که نقطه ای از این آمارگان فاصله گرفت آنرا به عنوان پـیش زمینـه اعـلام میکنند. در این دسته روش های گوناگونی جای میگیرند کـه مـا روش مـدل میـانگین  را بررسـی میکنیم .

-٢-٢-١ مدل میانگین

پروژه متلب برق :در این روش میانگین قاب های متوالی در طول زمانی محدود بدست آورده مـی شـود و بـه عنـوان تصویر زمینه در نظر گرفته می شود. سپس قدر مطلق تفریق تصویر هر قاب از آن محاسبه و با یک مقدار آستانه ، آستانه ای و نواحی حرکت استخراج می گردد [۵٢] و [۵٣].

در [۵٣]  از میانگین زمانی دنباله تصاویر برای بدست آوردن تصویر زمینه استفاده کرده اند. تـصویر

زمینه را در زمان t به صورت زیر بدست آورده اند:

B(x, y,t) =1  t∑I( x, y,t’)                                                            (۳-۳)

tt’=1

که (I)x, y, t مقدار پیکسل (x, y) در زمان t است . فرمول فوق به صورت زیر نیـز قابـل محاسـبه

میباشد:

B(x, y, t) =t1B(x, y, t−۱) +۱I(x, y, t)                    (۴-۳)

با تفریق تصویر از زمینه ، تـصاویر اشـیاء متحـرک بدست می آید که البته این تصویر با مقداری ثابت آستانه ای می شود.

روش میانگین زمانی دنباله تصاویر بسیار سریع است و برای استفاده در محیط های سربسته نتیجه خوبی بدست می دهد، اما نسبت به تغییرات نور، نویز و حرکت های جزیی در محیطهای سرباز مثل حرکت برگ درختان بسیار حساس است و نمی تواند تغییرات زمینه محیطهای سرباز را بـه خـوبی مدل کند.

٣-٣ تخمین حرکت به کمک شار نوری

دراین قسمت پدیده شار نوری تعریف میگـردد و سـپس معـادلات مربـوط بـه آن کـه یـک محدودیت بین گرادیانهای تصویر و بردارهای سرعت تحمیل میکنند بررسی میشـوند. بـسیاری از الگوریتمهای تخمین حرکت بر پایه همین معادلۀ مهم و اساسی میباشند. در ادامه ، روشهای معمول برای تخمین حرکت دو بعدی بیان شده و مشاهده خواهد شد که مشکل تخمین حرکت معمولاً بـه یک مسالۀ بهینه سازی مبدل میشود که شامل سه قسمت کلیدی است : پـارامتری کـردن میـدان حرکت ، فرمول بندی کردن معیار و ملاک بهینه سازی و جستجو برای پارامترهـای بهینـه . در ایـن فصل ، مگر در موارد خاص ، هرجا کلمه  “حرکت ”  بکار برده شود منظور حرکت دوُ بعدی است .

٣ ۴) شار نوری

٣-۴-١) حرکت دوبعدی و معادله شار نوری

پروژه متلب برق : چشم انسان ، حرکت را با استفاده از شناسایی نقاط متناسب در زمانهای مختلف درک میکند. ایـن تناسب معمولاً با استفاده از این فرض که شدت روشنایی یک نقطه پس از حرکت تغییـر نمـیکنـد

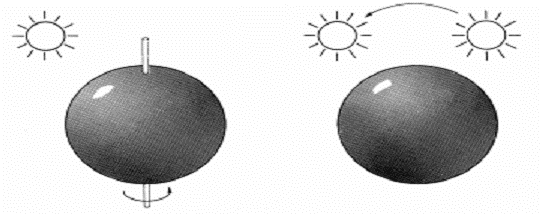
تعیین میشود. توجه شود که حرکت دوبعدی مشاهده شده میتواند با حرکت دوبعدی دیـده شـده واقعی تحت شرایط خاص متفاوت باشد. شکل ٣-٢ دو حالت خاص را نشان میدهد. در مثـال اول ، یک کره با سطح یکنواخت ، در حال چرخش حول محور کره و در یک محیط با روشنایی ثابت است .

از آنجا که هر نقطه روی کره ، رنگ یکسانی را بازتابش میکند، لذا چشم نمیتواند هـیچ تغییـری را در الگوی رنگ کره تصویر شده مشاهده کند، بنـابراین کـره را بـه صـورت سـاکن و غیـر متحـرک مشاهده میکند. درمثال دوم ، کره ثابت و غیر متحرک است ولی با استفاده از یک منبـع روشـنایی نقطه ای که در حال چرخش حول کره میباشد روشن شده است . حرکت منبع نـور باعـث حرکـت ناحیه بازتابش نور روی کره میشود که   میتواند باعث این تصور نادرست در چشم شودکه کره در حال چرخش است .

در ادبیات بینایی ماشین حرکت دو بعدی مشاهده شده تحت عنوان شار نوری بیان میشـود.

ولی مثالهای بالا نشان دادند که شار نوری ممکن است با حرکت دو بعـدی واقعـی یکـسان نباشـد.

زمانی که تنها اطلاعات رنگ تصویر در دسترس است و هیچ اطلاع دیگری راجع به نحوه حرکت در دسترس نیست ، روش امید بخش تخمین حرکت ، پدیده شار نوری یعنی مبنـا قـرار دادن مـشاهده است . در ادامۀ این فصل ، عبارت  “حرکت دو بعدی”  یا به طور ساده تـر عبـارت “حرکـت ”  بـرای اشاره به شار نوری بکار میرود. ممکن است در بعضی مواقع ، شار نوری بـا حرکـت دوبعـدی واقعـی متفاوت باشد.

شکل ٣-٢: دو مثال برای ارزیابی تفاوت حرکت واقعی با حرکت مشاهده شده [١]

٣-۴ ٢) معادله شار نوری و ابهام در تخمین حرکت

یک دنبالۀ ویدیویی که تغییرات روشنایی در آن با تابع (ψ)x, y,t بیـان مـیشـود را در نظـر

بگیرید. فرض کنید نقطه تصویر (x, y) در زمان t بـه نقطـه (    x) در زمـان t+d حرکـتt +d x, y+d yمیکند. تحت فرض شدت روشنایی ثابت ، تصاویر یک نقطۀ یکسان در زمانهای متفاوت دارای مقدار

-۵) کلیات تخمین حرکت یک شئ

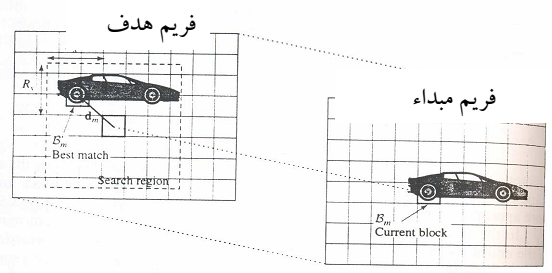
تخمین حرکت برای یک نقطـه خـاص بـین دو فـریم یعنـی ( ,  , ) و (  ,  , ) را در نظـر ψ x y t2  ψ x y t1 بگیرید. بردار حرکت بین دو زمان t و  t در نقطۀ مربوطه به عنوان جابه جایی این نقطه از زمان t تا زمان  t تعریف میشود. فریم مربوط به زمان t، فریم مبدأ یا اصطلاحاً فریم لنگـر١۵ و فـریم  مربوط به زمان  t ، فریم هدف ١۶ نامیده میشود. توجه کنید که فریم مبدأ لزوماً قبل از فریم هدف

قرار ندارد و بسته به نوع کاربرد، میتواند قبل یا بعد از فریم هدف باشد. مطابق شکل ٣-۵ زمانی که t>t باشد، عنوان تخمین حرکت روبه جلو١٧ و زمانی که t<t باشد، عنوان تخمـین حرکـت رو عقب ١٨ بکار برده میشود. برای سهولت ، فریمهای مبدأ و هدف بـه ترتیـب بـا ψ۲   x   ψ۱   x نشان داده میشود.

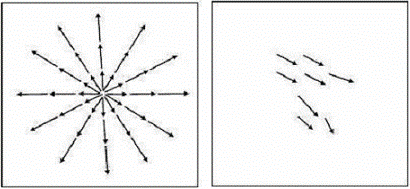به طور کلی، میتوان گفت که بردار حرکت در واقع یک بردار به صورت (d)x;a است که a ،یک بردار شامل کلیه پارامترهای حرکت و به صـورت T[ ]  مـیباشـد. بنـابراین تـابع

a = a1 a2  aL نگاشت متناظر با چنین بردار حرکتی نیز میتوانـد بـه صـورت (x;a)d + =w)x;a(  نـشان داده شود. تخمین حرکت در واقع تخمین بردار پارامترهای حرکت یعنی a است .

روشهایی که تاکنون برای تخمین حرکت مورد استفاده قرار گرفته اند را میتوان به دو گـروه اصلی طبقه بندی کرد:

ـ روشهای مبتنی بر ویژگی ١٩ـ روشهای مبتنی بر شدت روشنایی

در روشهای مبتنی بر ویژگی، نخست مشخصاتی مانند نقطه ، خط ، گوشه و غیره انتخاب شده و در دو فریم جستجو میشوند. سپس تناسبهایی بین دو مشخصۀ یافـت شـده در دو فـریم برقـرار میگردد. آنگاه با استفاده از این تناسبها، پارامترهای مدل حرکت انتخاب شده بدست میآیند.

روشهای مبتنی بر شدت روشنایی، از فرض روشنایی ثابت یا معادله شار نوری درهـر پیکـسلاستفاده میکنند و حرکت را براساس ارضاء این معادله (تا جایی که ممکن است ) تخمین میزنند.این روش زمانی که حرکت نمیتواند به صورت یک مدل ساده بیان شده و مـشخص گـردد وتخمین میدان حرکت پیکسل یا بلوک مورد نیاز میباشد، بسیار مناسب است .

روشهایی که درادامه بیان میشـوند، همگـی مبتنـی بـر روشـنایی بـوده و دارای کاربردهـای گسترده ای در پیش بینی وجبران حرکت هستند. به طور کلی، مسأله تخمـین حرکـت بـر اسـاس شدت روشنایی    میتواند به یک مسأله بهینه سازی که در آن سه پرسش کلیدی باید پاسـخ دادهشوند تبدیل شود:

١)     چگونه میدان حرکت را پارامتری کنیم ؟

٢)     چه معیاری را برای تخمین پارامترها استفاده کنیم ؟

٣)     چگونه پارامترهای بهینه را جستجو کنیم ؟

در این قسمت ، نخست چندین روش برای بیان یک میـدان حرکـت توضـیح داده مـیشـود و سپس معیارهای مختلف تخمین معرفی شده و در نهایت استراتژیهای جستجویی کـه عمـدتاً بـرای تخمین حرکت بکار میروند بیان میشود.

٣-۶) نمایش حرکت

یک مسأله کلیدی درتخمین حرکت ، نحوه پارامتری کردن میدان حرکت است . میدان حرکت

دو بعدی ناشی از حرکت یک شئ یا حرکت دوربین را معمـولاً مـیتـوان بـا چنـد پـارامتر محـدود

مشخص کرد و یک نمایش حرکت سرتاسری ٢١ را برای مشخص کردن میدان حرکت بکار بـرد. امـا این روش ، زمانی کارایی دارد که تنها دوربین در حال حرکت است و یـا صـحنۀ تـصویر شـده تنهـا شامل یک شئ متحرک مسطح میباشد.

ولی از آنجا که معمولاً چندین شئ متحرک کـه دارای حرکتهـای مختلفـی هـستند در یـک صحنۀ تصویر شده وجود دارند، لذا تنها استفاده از مدل پارامتری سرتاسری در اغلب مواقع مناسـب نیست . در واقع ساده ترین روش که هیچ محدودیتی ندارد، تخصیص یک بردار حرکت به هر پیکسل است . به این روش ، بازنمایی حرکت براساس پیکسل ٢٢ گفته میشود. این روش قابل کـاربرد اسـت ، ولی نیاز به تخمین تعداد مجهولهای زیادی به اندازه دو برابر تعداد پیکسلها برای تخمین حرکت در دو جهت x وy دارد.

به طور کلی، برای صحنه های شامل چندین شئ متحرک، بهتر اسـت یـک فـریم تـصویر بـه چندین ناحیه تقسیم شود، به گونه ای که حرکت در داخل هر ناحیه را بتوان به خوبی از طریق یک مدل پارامتری مشخص کرد. این روش تحت عنوان بازنمایی حرکت بر پایۀ ناحیه ٢٣ شناخته میشود و شامل یک الگوی ناحیه بندی٢۴ و چندین مجموعه پارامترهای حرکت که هر کدام به یـک ناحیـه تخصیص دارند میباشد. مشکل یک چنین روشی این است که شخص هیچ اطلاعی از اینکه تعدادی از پیکسلها دارای حرکت مشابهی هستند ندارد. لذا ناحیه بندی و تخمین حرکت در هر ناحیه بایـد به طور متوالی انجام شود که نیاز به محاسبات زیادی دارد و ممکن است در عمل مطلوب نباشد.

یک راه حل برای کاهش پیچیدگی محاسبات روش فوق ، استفاده از یک الگوی ناحیـه بنـدی ثابت است که تصویر را به تعدادی زیادی بلوک کوچک تقسیم میکند، به گونه ای که هر بلوک بـه اندازه کافی کوچک بوده و حرکت در داخل هر بلوک را میتوان به خوبی با یک مدل ساده توصـیف کرد و پارامترهای حرکت را به طور مستقل تخمین زد. این روش تحت عنوان بازنمایی حرکت برپایۀ بلوک ٢۵ شناخته     میشود. ساده ترین مدل حرکت در هر بلوک، یک انتقال ثابت است به گونه ای که مساله تخمین حرکت به یافتن یک بردار حرکت برای هر بلوک محدود میشود. از آنجا که ایـن روش سادگی و دقت قابل قبولی به دنبال دارد، در سیستمهای ویدیویی موفقیت زیادی کسب کرده است .یک مشکل مهم این روش ، عدم تحمیل تمهیدات لازم بر روی بردارهای حرکـت تخمـین زده شده در بلوکهای مجاور است . لذا حرکت شناسایی شده با این روش اغلب دارای عدم پیوسـتگی در مرزهای بلوکها، حتی در مواقعی که میدان حرکت به طور یکنواخت از بلوکی به بلوک دیگـر تغییـر کرده است   میباشد. روش بلوک، روی نواحی داخلی یک شئ که معمولاً دارای حرکت پیوسته ای هستند بسیار مناسب است . ولی برای شناسایی حرکتهای ناپیوسته در مرزهای شـئ از کـارائی لازم برخوردار نیست .

راه حل فائق آمدن بر این مشکل ، استفاده از روش بازنمایی حرکت بر پایـۀ مـش ٢۶ اسـت . در این روش ، فریم تصویر به نواحی فاقد همپوشانی تقسیم میشود و میدان حرکـت روی کـل تـصویر تنها با استفاده از بردارهای حرکت در نقاط گوشۀ نواحی مختلف که اصطلاحاً بـه آنهـا گریـد گفتـه میشود توصیف میگردد. در این روش بردارهای حرکت نقاط داخلی هر ناحیه از بردارهای حرکـت نقاط گوشه مجزا    میشوند. حاصل این روش ، میدان حرکتی است که همه جا پیوسته میباشد.

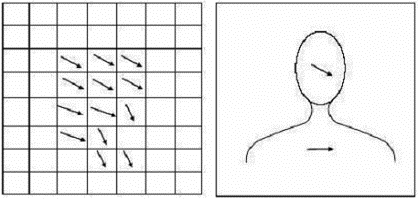
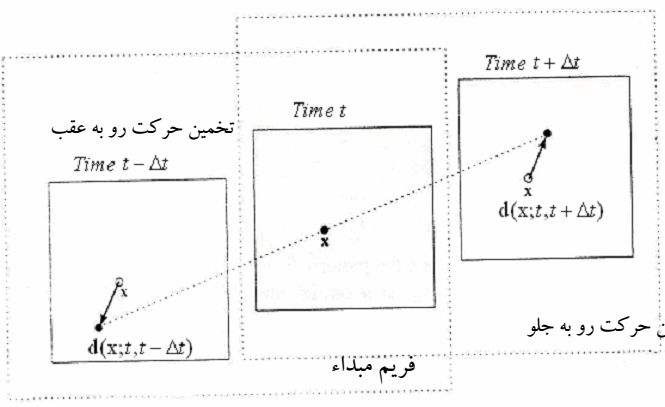
شکل ٣-۶ عملکرد روشهای فوق بر روی یک تصویر شامل سر و شانۀ یک انسان را نشان می- دهد. شکلهای (الف )، (ب )، (ج ) و (د) به ترتیب نمایشهای حرکت سرتاسری، پیکسل ، بلوک و ناحیه هستند.

شکل ٣-۶: انواع نمایشهای حرکت بر روی یک تصویر شامل سر و شانۀ یک انسان

(الف ) سرتاسری (ب ) پیکسل (ج ) بلوک (د) ناحیه [١]

٣-٧) معیار تخمین حرکت مسأله اساسی برای یـک مـدل حرکـت انتخـاب شـده، نحـوه تخمـین پارامترهای مدل است . در این قسمت ، چندین معیار مختلف برای تخمین پارامترهـای حرکـت بیـان می شود.متداول ترین معیار تخمین حرکت ، تفاضل مقادیر روشنایی هر جفت نقطه متناسب در فـریم مبدأ ψ و فریم هدف ψ است . یادآوری می شود که نقطه  xدر فریم ψ به  ( wx;a  ψ )حرکت می کند. بنابراین تابع ویژگی می تواند به صورت زیر نوشته شود:

البته همواره این گونه نیست که مینیمم سازی تابع خطای DFD و یا معادله  شار نوری منجر به یک تخمین حرکت با معنی از لحاظ فیزیکی شود. این اساساً به ایـن دلیـل اسـت کـه در عمـل ، فرض شدت روشنایی ثابت همواره صحیح نیست . شدت روشنایی یک نقطه خاص شئ ممکن اسـت پس از حرکت شئ به علت تغییر اثرات انعکاس نور و سایه ها تغییر کند. دلیل دوم این است که در یک ناحیه مسطح ، تخمین حرکتهای بسیار متفاوتی میتوانند در فـرض شـدت روشـنایی ثابـت یـا معادله شار نوری صدق کنند. نهایتاً اگر حرکت در هر پیکسل را فقط با بردارهای حرکت و بدون در نظر گرفتن پارامترهای مربوط به حرکت توصیف کنیم ، آنگاه معادلـه شـار نـوری کـاملاً نمـیتوانـد بردارهای حرکت را محدود کرده و الزامات لازم را روی آنها قرار دهد. این فاکتورها میتوانند تخمین حرکت را به یک مشکل لاینحل تبدیل کنند. برای دستیابی به راه حل معقول فیزیکـی در تخمـین حرکت ، باید از شروط و تمهیدات اضافی بر روی تخمین حرکت استفاده کرد.

یک ویژگی میدان حرکت این است که به جز در مرزهای اشیاء معمولاً بـه طـور یکنواخـت از پیکسلی به پیکسل دیگر تغییر میکند. برای منظور کردن ایـن اثـر یکنـواختی مـیتـوان از انـدازه اختلاف بین بردارهای حرکت پیکسلهای مجاور در یک همسایگی چهار یـا هـشت پیکـسل x بـه تخمین حرکت بر پایه پیکسلدر روش تخمین حرکت بر پایه پیکسل ، برای هر پیکسل یک بردار حرکت تخمـین زده مـی- شود. اما واضح است که این روش به درستی تعریف نشده است ؛ زیرا اگر یک پیکسل خاص در نظـر گرفته شده و از فرض شدت روشنایی ثابت برای هر پیکـسل در فـریم مبـدأ اسـتفاده شـود، تعـداد زیادی پیکسل در فریم هدف وجود دارند که دقیقاً شدت روشنایی یکسانی با پیکسل مربوطه دارنـد و اگر از معادله شار نوری استفاده شود، هنوز مشکل باقی اسـت ، زیـرا بـرای دو مجهـول تنهـا یـک معادله وجود دارد. برای حل این مشکل ، به طور کلی چهار راه حل وجود دارد [١]:

١) میتوان از تکنیکهای یکنواخت سازی روی میدان حرکت استفاده کـرد، بـه گونـه ای کـه میدان حرکت یک پیکسل جدید متأثر از بردارهای حرکت یافت شده بـرای پیکـسلهای اطـراف آن باشد.

٢) میتوان فرض کرد که بردارهای حرکت در یـک همـسایگی اطـراف هـر پیکـسل یکـسان

هستند و فرض شدت روشنایی ثابت و یا معادله شار نوری را روی کل همسایگی بکار برد [۶].

٣) استفاده از تمهیدات اضافی علاوه بر فرض شدت روشنایی ثابت ؛ مثلاً استفاده از این فـرض

که گرادیان شدت روشنایی در حین حرکت ثابت و بدون تغییر است [٧،٨،٩،١٠].

۴) استفاده از تناسب بین توابع فاز فریم در قبل و بعد از حرکت [٧] .

٣-١١) الگوریتم تطبیق بلوک

مشاهده شدکه یک راه حل برای مشکل تخمین حرکت بر پایـه پیکـسل ، تحمیـل تمهیـدات یکنواختی است . یک روش تحمیل تمهیدات یکنواختی روی میدان حرکت تخمینی، تقـسیم حـوزه تصویر به نواحی کوچک بدون همپوشانی به نام بلوک است و با ایـن فـرض کـه میـدان حرکـت در داخل هر بلوک میتواند بوسیله یک مدل پارامتری ساده برای مثال مدل انتقال ثابت ، مـدل affine و یا مدل bilinear بیان شود. اگر بلوکها به اندازه کافی کوچک باشند، ایـن روش مـیتوانـد کـاملاً دقیق باشد. دراین قسمت ، الگوریتمهای تخمین حرکت که از نمایش حرکت بر پایه بلـوک اسـتفاده میکنند توضیح داده میشوند.

اگر B نشان دهنده mُ امین بلوک تصویر و M تعـداد بلوکهـا باشـد و {M,…,1,2}=m،آنگـاه m بلوکها باید در شرط زیر صدق کنند:

الگوریتمهای جستجوی سریع

واضح است که الگوریتم تطبیق بلوک که در بالا توضیح داده شد، نیـاز بـه محاسـبات زیـادی دارد. برای مثال ، در یک ناحیۀ جستجوی R ± و با گامهای به انـدازه یـک پیکـسل ، تعدادکاندیـدها ٢(١+ R ٢) است که نشان دهنده حجم بالای محاسبات میباشـد. کلیـد کـاهش محاسـبات ، کـاهش تعداد کاندیدها است که برای میسر شدن این امر و برای سرعت بخشیدن به جستجو، الگوریتمهـای جستجوی سریع متعددی برای تطبیق بلوکها پدیـد آمـده انـد. در ادامـه ، بـه توضـیح دو نمونـه از مهمترین الگوریتمهای جستجوی سریع پرداخته میشود.

٣-١٣) روش جستجوی D-log-2

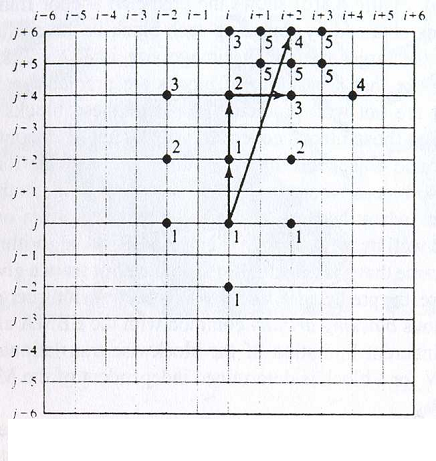
یک الگوریتم جستجوی سریع ، الگوریتم D-log-2 [١١] مطابق شکل ٣-٨ است . این الگوریتم ، جستجو را با مکانی با جابه جایی صفر شروع کرده و در هر مرحله ، پنج نقطه را بررسی و تست می – کند. در مرحله بعد، جستجو با مرکز حرکت داده شده به بهترین نقطۀ منطبق بدست آمده از مرحله قبل تکرار میشود. اندازه گامهای جستجو در مراحل مختلف ثابت باقی میمانند، مگر اینکه بهترین نقطۀ تطبیقی، نقطۀ مرکزی پنج نقطۀ بررسی شده باشـد و یـا مکـان جـستجودر مـاکزیمم شـعاع جستجو قرار داشته باشد که در این حالت اندازه گامها کاهش مییابد. از طرف دیگر مرحلـۀ نهـایی زمانی است که گام جستجو، به یک پیکسل کاهش یابد که در این مرحلـۀ آخـر، ٩ نقطـۀ جـستجو مورد بررسی قرار میگیرند. اندازه گام ابتدایی را معمولاً نصف ماکزیمم شعاع جستجو قرار میدهند.

عیب این روش این است که نمیتوان تعداد مراحل و به تبع تعداد کل نقاطی کـه بررسـی خواهنـد شد را از قبل تعیین کرد.

روش جستجوی سه گام

یک الگوریتم جستجوی سریع دیگر، الگوریتم سـه گـام [١٢] مطـابق شـکل ٣-٩ اسـت . ایـن الگوریتم ، جستجوی را با اندازه گام برابر یا بزرگتر از نصف ماکزیمم شعاع جستجو شروع کـرده و در این مرحله ٩ نقطه را تست و مقایسه میکند. اندازه گام جستجو بعد از هر مرحله نصف مـیشـود و جستجو با اندازه گام یک پیکسل خاتمه مییابد. در هر مرحله جدید، مرکز جستجو به بهترین نقطه تطبیقی بدست آمده از مرحلۀ قبل حرکت داده میشود. به جز مرحله اول که ٩ نقطه بررسی مـی- شود، در مراحل بعدی هشت نقطه مورد بررسی قرار میگیرند. لذا کـل تعـداد نقـاط بررسـی شـده ١+ ۸L است که L تعداد مراحل بوده و به اندازه گام جستجوی ابتدایی بستگی دارد. برخلاف روش جستجوی D-log-2 ، در روش سه گام تعداد مراحل و تعداد نقاطی که بررسی خواهند شد از قبـل قابل پیش بینی است . بـه عـلاوه ایـن روش سـاختار مـنظم تـری نـسبت بـه روش  D-log-2 دارد.

همچنین برای مثال با یک رنج جستجوی ٣٢= R و با روش تطبیـق بلـوک، تعـداد نقـاط جـستجو ۴٢٢۵ است ، در حالی که با روش سه گام ، تعداد نقاط به ۴١ کاهش مییابد. ایـن مشخـصات باعـث شده است روش سه گام ، از نظر الگوریتمهای جستجوی سریع و همچنین از نظر پیاده سازی VLSI بیشتر مورد توجه قرار گیرد.

مقایسۀ الگوریتمهای جستجو

جدول ٣-١، تعداد مراحل جستجو و مینیمم و ماکزیمم تعداد نقاطی که باید بررسی شوند را در سه الگوریتم جستجوی مختلف که در قسمتهای قبل توضیح داده شدند و برای رنج جستجوی    نـشان میدهد. مشاهده میشود که در روش جستجوی معمولی استفاده شده در الگوریتم تطبیـق بلـوک، باید ٢٢۵ نقطه بررسی شود که این حجم بالای محاسبات را نشان میدهد. در صورتی که تعداد این نقاط در روش جستجوی D-log-2 به ماکزیمم ٢۶ نقطه و در روش جستجوی سه گام به ٢۵ نقطه کاهش مییابد. تفاوت دیگری که در جدول ٣-١ مشهود میباشد این است که تعداد نقـاط بررسـی شده و تعداد مراحل در روش سه گام ثابت و قابل پیش بینی است ، در حالی که در مـورد روش -٢ D-log چنین نیست .

الگوریتمهای تطبیق بلوک تغییر پذیر

در الگوریتم تطبیق بلوک که در قسمت قبل توضیح داده شد، فرض شده است که هـر بلـوک فقط دارای یک حرکت انتقالی و بدون هیچ تغییر شکلی باشد. اما این مدل برای بلوکهایی که دارای حالت چرخش ، زوم و غیره هستند مناسب نیست . لـذا بایـد مـدلهای حرکـت مناسـب تـری ماننـد Bilinear ،Affine  و یا projective mapping برای تشریح حرکت هر بلوک استفاده شود. البتـه واضح است که این مدلهای حرکت ، مدل حرکت انتقالی را نیز به عنوان یک حالـت خـاص پوشـش میدهند. بااین مدلها، یک بلوک مربعی در فریم مبدأ مطابق شکل ٣-١٠ به یک چهـار ضـلعی غیـر مربعی در فریم هدف متناظر میشود. بنابراین ، دسته ای از روشهای تخمین حرکت بر پایۀ بلوک را که از مدلهای درجه بالاتر استفاده میکنند، الگوریتمهای تطبیق بلوک تغییر پذیر مینامند.