حل مساله فروشنده دورگرد و مساله چند وزیر با الگوریتم جستجو ممنوعه در متلب
حل مساله فروشنده دورگرد و مساله چند وزیر با الگوریتم جستجو ممنوعه tabu search در متلب :پروژه متلب
پروژه متلب :
الگوریتم جستجوی ممنوعه (Tabu Search) (TS) یک الگوریتم بهینهسازی فراابتکاری است که برای اولین بار در سال ۱۹۸۶ توسط گلووِر Glover معرفی شد.در سال ۱۹۹۷، اولین کتابی که کاملاً به جستجوی ممنوعه اختصاص داشت توسط گلووِر و لاگونا منتشر شد. واژهٔ تابو از تُنگان زبان مردم جزایر پلینزی در اقیانوس آرام گرفته شدهاست. این واژه به معنای شیء مقدسی است که به دلیل قداست نباید آن را لمس کرد. بر اساس واژهنامهٔ وِبستر، امروزه این واژه در معنای «ممنوعیت ایجاد شده به دلیل فرهنگ اجتماعی برای ایجاد اقدام حفاظتی» یا «ممنوعیت چیزی که دارای ریسک است»، به کار میرود.معنای اخیر واژهٔ تابو، با تکنیک جستجوی ممنوعه کاملاً سازگار است. پروژه متلب ریسکی که در الگوریتم جستجوی ممنوعه از آن اجتناب میشود، خطر مسیرهای نامناسب است.
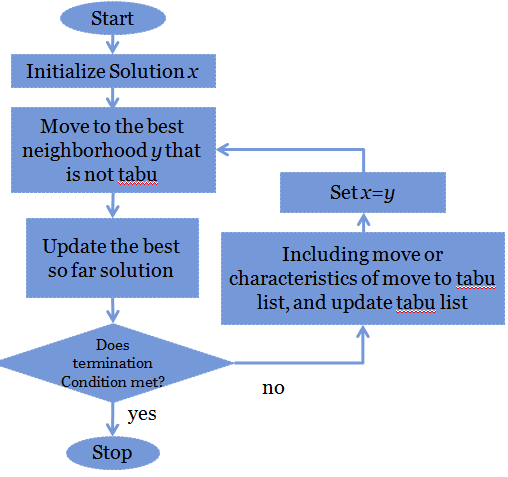
ساختار کلی جستجوی ممنوعه
پروژه متلب برای رسیدن به جواب بهینه در یک مسئله بهینهسازی، الگوریتم جستجوی ممنوعه ابتدا از یک جواب اولیه شروع به حرکت میکند. سپس الگوریتم بهترین جواب همسایه را از میان همسایههای جواب فعلی انتخاب میکند. در صورتی که این جواب در فهرست ممنوعه قرار نداشته باشد، الگوریتم به جواب همسایه حرکت میکند؛ در غیراینصورت الگوریتم معیاری به نام معیار تنفس را چک خواهد کرد. بر اساس معیار تنفس اگر جواب همسایه از بهترین جواب یافت شده تا کنون بهتر باشد، الگوریتم به آن حرکت خواهد کرد، حتی اگر آن جواب در فهرست ممنوعه باشد. پس از حرکت الگوریتم به جواب همسایه، فهرست ممنوعه بروزرسانی میشود؛ به این معنا که حرکت قبل که بوسیلهٔ آن به جواب همسایه حرکت کردیم در فهرست ممنوعه قرار داده میشود تا از بازگشت مجدد الگوریتم به آن جواب و ایجاد سیکل جلوگیری شود. در واقع فهرست ممنوعه ابزاری در الگوریتم جستجوی ممنوعهاست که توسط آن از قرار گرفتن الگوریتم در بهینهٔ محلی جلوگیری میشود. پس از قرار دادن حرکت قبلی در فهرست ممنوعه، تعدادی از حرکتهایی که قبلاً در فهرست ممنوعه قرار گرفته بودند از فهرست خارج میشوند. مدت زمانی که حرکتها در فهرست ممنوعه قرار میگیرند توسط یک پارامتر که زمان ممنوعه (tabu tenure) نام دارد تعیین میشود. حرکت از جواب فعلی به جواب همسایه تا جایی ادامه مییابد که شرط خاتمه دیده شود. شرطهای خاتمه متفاوتی میتوان برای الگوریتم در نظر گرفت. بهطور مثال محدودیت تعداد حرکت به جواب همسایه میتواند یک شرط خاتمه باشد.
استراتژیهای پیشرفتهٔ جستجوی ممنوعه
ساختار کلی جستجوی ممنوعه اغلب جوابگوی مسائل بزرگ نیست؛ بنابراین به منظور افزایش قدرت الگوریتم از استراتژیهای زیر که معروف به استراتژیهای پیشرفته جستجوی ممنوعه هستند استفاده میشود:
- استراتژی فهرست کاندید(Candidate List Strategy): در یک TS عادی، برای حرکت از یک جواب فعلی به یک جواب همسایه، باید مقدار تابع هدف برای هر عنصر از همسایهها ارزیابی شود. این کار میتواند از لحاظ محاسباتی بسیار هزینه بر باشد. روشی دیگر، این است که به جای آن که تمامی همسایهها بررسی شود، تنها یک زیرمجموعهٔ تصادفی از همسایهها در نظر گرفته شود، که در نتیجه هزینهٔ محاسباتی بهطور قابل ملاحظهای کاهش مییابد. انتخاب زیرمجموعهای از جوابهای همسایه به صورت تصادفی، میتواند به عنوان یک مکانیزم ضد چرخه عمل کند؛ این کار اجازه میدهد که از فهرست ممنوعهٔ کوچکتری نسبت به کل همسایگی، استفاده شود. البته باید در نظر داشت که این کار یک عیب مهم دارد و آن احتمال از دست دادن جوابهای خوب است، بنابراین احتمالهایی را نیز میتوان به کار برد تا معیارهای ممنوعه فعال شود.
- استراتژی تقویت (Intensification Strategy): استراتژی تقویت به معنای یافتن حرکتهای خوب و افزایش انجام آن حرکتها در الگوریتم است. تقویت، در بسیاری از پیادهسازیهای TS استفاده میشود، اما همیشه ضروری نیست، زیرا حالتهای بسیاری وجود دارد که در آنها جستجوی معمولی کفایت میکند.
- استراتژی تنوع بخشی (Diversification Strategy): روشهای مبتنی بر جستجوی محلی، آنقدر محلی هستند که زمان زیادی یا تمامی زمان خود را در بخش محدودی از فضای جستجو صرف میکنند. نتیجهای که از این واقعیت میتوان گرفت، این است که هر چند جوابهای خوبی به وسیلهٔ این روشها به دست میآید، اما ممکن است جستجو از اکتشاف مناطق بهتر باز بماند و بنابراین به جوابهایی برسد که از جواب بهینه، بسیار دور هستند. تنوعبخشی، یک مکانیزم الگوریتمیک است که برای حل این مشکل تلاش میکند. برای انجام این کار، تنوعبخشی، جستجو را مجبور میکند به سوی مناطقی که تا کنون کشف نشده، حرکت کند.
- مجوز دادن به جوابهای نشدنی: در حالتهایی که محدودیتهای مسئله بسیار محدودکننده باشند و از جستجوی مؤثر فضای جواب جلوگیری کنند از این استراتژی استفاده میشود. طی این استراتژی محدودیتهای مسئله آزاد شده و بجای آنها یک مقدار جریمه به تابع هدف اضافه میشود.
مسئله چند وزیر یک معمای شطرنجی و ریاضیاتی است که بر اساس آن باید n وزیر شطرنج در یک صفحه n×n شطرنج بهگونهای قرار داده شوند که هیچیک زیر ضرب دیگری نباشند. با توجه به اینکه وزیر بهصورت افقی، عمودی و اُریب حرکت میکند، باید هر وزیر را در طول، عرض و قطر متفاوتی قرار داد.
اولین و مشهورترین شکل این مسئله معمای هشت وزیر است که برای حل آن باید ۸ وزیر را در یک صفحهً معمولی (۸×۸) شطرنج قرار داد. این مسئله ۹۲ جواب دارد که ۱۲ جواب آن منحصر بهفرد است یعنی بقیه جوابها از تقارن جوابهای اصلی بهدست میآید.
مسئله n وزیر در صورتی جواب دارد که n مساوی ۱ یا بیشتر از ۳ باشد. یعنی مسئله دو وزیر و سه وزیر راه حلی ندارند.
الگوریتم عقبگرد
پروژه متلب : از تکنیک عقبگرد Backtracking برای حل مسائلی استفاده میشود که در آنها دنبالهای از اشیاء از یک مجموعه مشخص انتخاب میشود، بهطوریکه این دنباله، ملاکی را در بر میگیرد. عقبگرد حالت اصلاح شدهٔ جستجوی عمقی یک درخت است. این الگوریتم همانند جستجوی عمقی است، با این تفاوت که فرزندان یک گره فقط هنگامی ملاقات میشوند که گره امید بخش باشد و در آن گره حلی وجود نداشته باشد. با توجه به اینکه هیچ ۲ وزیری نباید همدیگر را گارد کنند و در یک سطر نمیتوانند باشند، تعداد کل حالتها برای n=۴ برابر ۴*۴*۴*۴=۲۵۶ است. در شطرنج یک وزیر میتواند به مهرههایی که در خانههای عمود یا مورب به وی قرار دارند حمله کند. یا به عبارت ریاضی، اگر ردیفها و ستونهای شطرنج را از یک تا هشت شمارهگذاری کنیم و وزیر در خانه (i، j) قرار داشته باشد، مهرههایی که در خانههای (i، m) یا (m، j) یا (i ± m، j ± m) قرار دارند توسط وزیر تهدید میشوند.
برای سادگی تشریح این مسئله با استفاده از روش بازگشت به عقب، فرض میکنیم که خانههای شطرنج ۴x۴ و تعداد وزیرها نیز ۴ باشد. سپس بعد از یافتن راه حل برای این مسئله ساده شده، اقدام به نوشتن الگوریتم برای مسئله اصلی میکنیم.
مراحل جستجو برای یافتن جواب را به این صورت دنبال میکنیم که: وزیر اول را در ردیف اول و ستون اول قرار میدهیم.
پروژه متلب در ردیف دوم از اولین ستون به جلو رفته و به دنبال خانهای میگردیم که مورد تهدید وزیر اول نباشد و وزیر دوم را در این خانه قرار میدهیم.
همانند قبل، در ردیف سوم از اولین ستون به جلو رفته و به دنبال خانهای میگردیم که مورد تهدید وزیران اول و دوم نباشد. میبینیم که چنین خانهای موجود نیست. پس به عقب یعنی ردیف دوم برگشته و وزیر دوم را به خانهای دیگر از ردیف دوم منتقل میکنیم که مورد تهدید وزیر اول نباشد.
دوباره در ردیف سوم اولین خانهای را میابیم که مورد تهدید دو وزیر قبلی نباشد. این بار خانه را مییابیم و وزیر سوم را در آن قرار میدهیم.
همانند قبل، در ردیف چهارم به دنبال اولین خانهای میگردیم که مورد تهدید وزیران پیشین نباشد. چنین خانهای موجود نیست. به ردیف قبل یعنی ردیف سوم باز میگردیم تا خانهای دیگر برای وزیر سوم بیابیم. خانه دیگری وجود ندارد. به ردیف قبل یعنی ردیف دوم بر میگردیم تا خانه دیگری برای وزیر دوم پیدا کنیم. به آخرین ستون رسیدهایم و خانه دیگری نیست. به ردیف قبل یعنی ردیف اول بر میگردیم و وزیر اول را یک ستون به جلو میبریم.
در ردیف دوم اولین خانهای را میابیم که مورد تهدید وزیر اول نباشد و وزیر دوم را در آن خانه قرار میدهیم.
در ردیف سوم اولین خانهای را میابیم که مورد تهدید وزیران اول و دوم نباشد و وزیر سوم را در آن خانه میگذاریم.
در ردیف چهارم اولین خانهای را میابیم که مورد تهدید وزیران پیشین نباشد. این بار خانه را مییابیم و وزیر چهارم را در آن خانه قرار میدهیم.
پروژه متلب به یک جواب میرسیم. حال اگر فرض کنیم که این خانه جواب نیست و به مسیر خود ادامه دهیم، احتمالاً” میتوانیم جوابهای دیگری نیز بیابیم.
مسئله فروشنده دورهگرد (به انگلیسی: Travelling salesman problem، بهاختصار: TSP) مسئلهای مشهور است که ابتدا در سده ۱۸ مسائل مربوط به آن توسط ویلیام همیلتون و چوریو مطرح شد و سپس در دهه ۱۹۳۰ شکل عمومی آن به وسیله ریاضیدانانی مثل کارل منگر از دانشگاه هاروارد و هاسلر ویتنی از دانشگاه پرینستون مورد مطالعه قرار گرفت.
شرح مسئله بدین شکل است که:
- تعدادی شهر داریم و هزینه رفتن مستقیم از یکی به دیگری را میدانیم. مطلوب است کمهزینهترین مسیری که از یک شهر شروع شود و از تمامی شهرها دقیقاً یکبار عبور کند و به شهر شروع بازگردد.
پروژه متلب تعداد جوابهای شدنی مسئله، برابر است با {\displaystyle {\frac {1}{2}}(n-1)!} برای n>۲ که n تعداد شهرها میباشد. در واقع این عدد برابر است با تعداد دورهای همیلتونی در یک گراف کامل با n رأس.
مسئله فروشنده دوره گرد یا Traveling Salesman Problem (به اختصار TSP)، یکی از مسائل بسیار مهم و پرکاربرد در علوم کامپیوتر و تحقیق در عملیات است.
سه روش کلی برای کد کردن راه حلهای مسئله TSP ارائه شدهاست که در الگوریتمهای مختلفی قابل استفاده هستند. راه حلهای سهگانه عبارتند از:
الف) نمایش جواب به صورت رشته گسسته جایگشتی که در الگوریتمهای زیر قابل استفاده است: الگوریتم ژنتیک یا Genetic Algorithms (به اختصار GA) شبیهسازی تبرید یا Simulated Annealing (به اختصار SA) جستجوی ممنوعه یا Tabu Search (به اختصار TS) جستجوی همسایگی متغیر یا Variable Neighborhood Search (به اختصار VNS) بهینهسازی کلونی مورچگان یا Ant Colony Optimization (به اختصار ACO) جستجوی هارمونی یا Harmony Search (به اختصار HS) و سایر الگوریتمهای بهینهسازی گسسته
ب) نمایش جواب به صورت کلیدهای تصادفی یا Random Key که در الگوریتمهای زیر قابل استفاده است: الگوریتم ژنتیک یا Genetic Algorithms (به اختصار GA) بهینهسازی ازدحام ذرات یا Particle Swarm Optimization (به اختصار PSO) الگوریتم رقابت استعماری یا Imperialist Competitive Algorithm (به اختصار ICA) تکامل تفاضلی یا Differential Evolution (به اختصار DE) بهینهسازی مبتنی بر جغرافیای زیستی یا Bio-geography Based Optimization (به اختصار BBO) استراتژیهای تکاملی یا Evolution Strategies (به اختصار ES) برنامهریزی تکاملی یا Evolutionary Programming (به اختصار EP) و سایر الگوریتمهای بهینهسازی پیوسته
پروژه متلب پ) نمایش جواب به شکل ماتریسهای شبیه فرومون که توسط تمامی الگوریتمهای اشاره شده در مورد (ب) قابل استفاده میباشد.
- مسئله معادل در نظریه گراف به این صورت است که یک گراف وزندار کامل داریم که میخواهیم کموزنترین دور همیلتونی را پیدا کنیم.
- مسئله تنگراه فروشنده دورهگرد (به انگلیسی: Bottleneck traveling salesman problem، بهاختصار: bottleneck TSP) مسئلهای بسیار کاربردی است که در یک گراف وزندار کموزنترین دور همیلتونی را میخواهد که شامل سنگینترین یال باشد.
- تعمیمیافته مسئله فروشنده دورهگرد دارای ایالتهایی است که هر کدام حداقل یک شهر دارند و فروشنده باید از هر ایالت دقیقاً از یک شهر عبور کند. این مسئله به «مسئله سیاستمدار مسافر» نیز شهرت دارد.
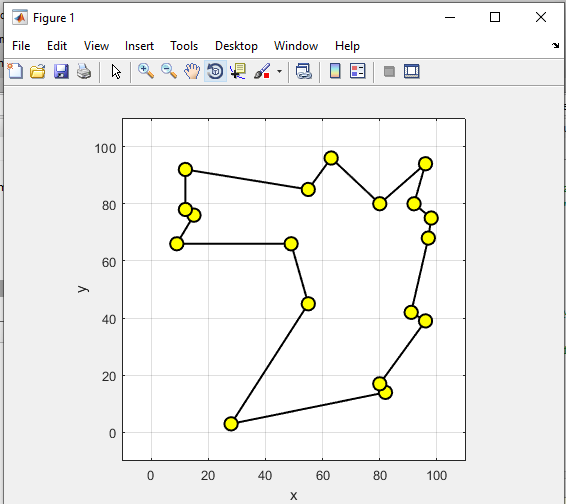
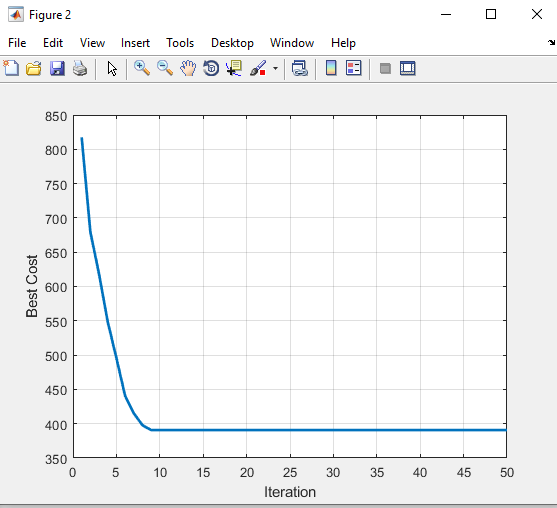
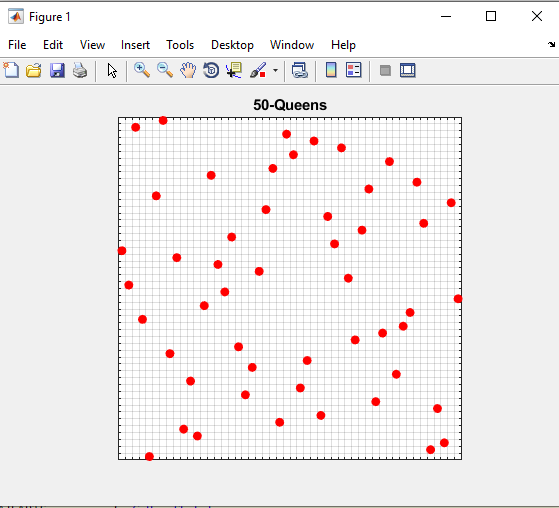
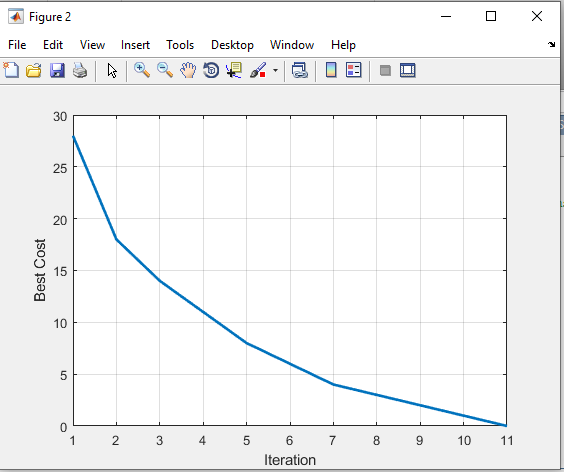
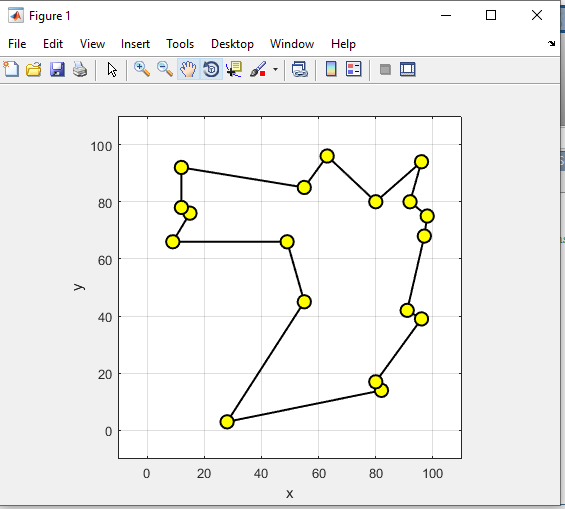
خروجی متلب :


لطفاً براي ارسال دیدگاه، ابتدا وارد حساب كاربري خود بشويد