مسیریابی هدف با کمک الگوریتمA* الگوریتم (A STAR) در متلب - انجام پروژه متلب |پروژه متلب | انجام پروژه متلب برق | شبیه سازی با متلب

مسیریابی هدف با کمک الگوریتمA* الگوریتم (A STAR) در متلب

مسیریابی در گراف با کمک الگوریتمA* الگوریتم (A STAR) در متلب :پروژه متلب

پروژه متلب :در علوم کامپیوتر، الگوریتم A* یک الگوریتم مسیریابی است که برای پیمایش و یافتن مسیر در گراف استفاده می‌شود. به علت عملکرد و دقت بالای این الگوریتم استفاده گسترده‌ای از آن می‌شود. پیتر ای هارت (به انگلیسی: Peter E. Hart)، نیلز نیلسون (Nils Nilsson) و برترام رافائل (Bertram Raphael) اولین کسانی بودند که آن را در سال ۱۹۶۸ میلادی شرح دادند. این الگوریتم در واقع تعمیمی از الگوریتم دیکسترا می‌باشد که با استفاده از روش‌های فرا ابتکاری عملکرد بهتری در زمینه جستجو بدست آورده‌است.

گربه‌‌‌‌ی مسیریاب

تصور کنید که ما یک بازی داریم که در آن گربه‌‌‌‌ای می‌‌‌‌خواهد مسیری را برای رسیدن به یک تکه استخوان پیدا کند.

شاید از خود بپرسید که یک گربه چرا باید به دنبال یک تکه استخوان باشد؟!

خوب! گربه‌‌‌‌ی بازیِ ما بسیار زیرک است و می‌‌‌‌خواهد با جمع کردن استخوان‌‌‌‌ها و دادن آن‌‌‌‌ها به سگ‌‌‌‌ها، از چنگال آن‌‌‌‌ها در امان بماند!

فرض کنید گربه‌‌‌‌ی موجود در شکل زیر می‌‌‌‌خواهد کوتاه‌‌‌‌ترین مسیر برای رسیدن به استخوان را پیدا کند:

متأسفانه گربه نمی‌‌‌‌تواند مستقیماً از مکان فعلی خود به طرف استخوان حرکت کند، چون در مقابلش یک دیوار قرار دارد و گربه‌‌‌‌ی ما هم برخلاف ارواح نمی‏‌تواند از دیوار عبور کند!

از طرف دیگر، گربه‌‌‌‌ی ما خیلی تنبل است و دوست دارد که کوتاه‌‌‌‌ترین راه را پیدا کند.

اما چگونه می‌‌‌‌توانیم الگوریتمی بنویسیم که کوتاه‌‌‌‌ترین مسیر بین گربه و استخوان را پیدا کند؟ اینجاست که از «آ-ستاره» کمک می‌‌‌‌گیریم!

ساده کردن حوزه‌‌‌‌ی جستجو

در گام نخست باید حوزه‌‌‌‌ی جستجو را به چیزی که مدلسازی ریاضی آن آسان باشد نزدیک کنیم.

مثلاً می‌‌‌‌توانیم حوزه‌‌‌‌ی جستجو را پیکسل‌‌‌‌بندی کنیم؛ اما در شرایط فعلی این کاملاً غیرضروری است و فقط کار ما را سخت می‌‌‌‌کند پس بهتر است به چیز ساده‌‌‌‌تری فکر کنیم مثلاً تقسیم‌‌‌‌بندی صفحه به مربع‌‌‌‌های هم اندازه و تا حد ممکن بزرگ. البته می‌‌‌‌توان واحدهای مختلفی برای تقسیم‌‌‌‌بندی صفحه (مثل مثلث یا شش‌‌‌‌‏ضلعی) به کار برد اما مربع آسان‌‌‌‌ترین و بهترین گزینه‌‌‌‌ای است که می‌‌‌‌توان برای این مسئله انتخاب کرد.

با این تقسیم‌‌‌‌بندی می‌‌‌‌توانیم حوزه‌‌‌‌ی جستجو را تبدیل به یک آرایه‌‌‌‌ی دو بعدی کنیم که مانند یک نقشه از حوزه‌‌‌‌ی جستجو، همه چیز را در اختیار ما می‌‌‌‌گذارد. مثلاً اگر سطح یک مربع کاشی شده‌‌‌‌ی ۲۵ در ۲۵ را در نظر بگیریم، حوزه‌‌‌‌ی جستجوی ما یک آرایه‌‌‌‌ی دوبعدی متشکل از ۶۲۵ کاشی مربعی‌‌‌‌شکل خواهد بود. حالا اگر در همین نقشه، بخواهیم از واحد پیکسل استفاده کنیم، حوزه‌‌‌‌ی جستجوی ما تبدیل به یک آرایه‌‌‌‌ی دوبعدی متشکل از ۶۴۰۰۰۰ مربع خواهد شد (با این فرض که ابعاد هر کاشی ۳۲×۳۲ پیکسل باشد)!

بهتر است پس از تقسیم‌‌‌‌بندیِ مربعیِ حوزه‌‌‌‌ی جستجو نگاهی به آن بیندازیم که حالا به یک صفحه با (۶×۷ کاشی =) ۴۲ کاشی مربعی‌‌‌‌شکل تبدیل شده است:

لیست‌‌‌‌های باز و بسته

حالاً که حوزه‌‌‌‌ی جستجو را به شکل ساده‌‌‌‌تری درآوردیم، زمان بحث در مورد الگوریتم آ-ستاره رسیده است.

گربه‌‌‌‌ی ما علاوه بر این که تنبل است، حافظه‌‌‌‌ی چندان خوبی هم ندارد، بنابر این ما به دو لیست نیاز داریم:

یکی برای فهرست کردن تمام مربع‌‌‌‌هایی که تصور می‌‌‌‌شود کوتاه‌‌‌‌ترین مسیر را به دست دهند؛ که آن را لیست باز (Open List) می‌‌‌‌نامیم.

دیگری برای فهرست کردن مربع‌‌‌‌هایی که دیگر لازم نیست مورد ارزیابی قرار گیرند که آن را لیست بسته (Closed List) می‌‌‌‌نامیم.

گربه با اضافه کردن موقعیت فعلی‌‌‌‌اش به لیست بسته، کارش را شروع می‌‌‌‌کند. (ما نقطه‌‌‌‌ی شروع را A می‏‌نامیم.) سپس از میان مربع‌‌‌‌های همسایه‌‌‌‌اش (Adjucent Squares) ، آن‌‌‌‌هایی را که قابل تردد هستند به لیست باز اضافه می‌‌‌‌کند.

این تصویر نمونه‌‌‌‌ای از چیزی است در بالا بیان شد، البته با این فرض که گربه در محیطی باز و بدون مانع قرار داشته باشد. (مربع‌‌‌‌های با حاشیه‌‌‌‌ی سبزرنگ همان لیستِ باز هستند):

حالا گربه باید مشخص کند که کدام یک از این مربع‌‌‌‌ها در کوتاه‌‌‌‌ترین مسیر قرار دارند. اما چگونه؟

خوب، در الگوریتم آ-ستاره این کار با اختصاص دادن امتیاز به هر مربع انجام می‌‌‌‌پذیرد که به آن امتیازدهی مسیر (Path Scoring) گفته می‏شود.

امتیازدهی به مسیر

ما به هر مربع یک امتیاز که حاصل جمع G+H است، اختصاص می‌‌‌‌دهیم:

G

‌هزینه‌‌‌‌‌ی حرکت از نقطه‌‌‌‌ی شروع مسیر تا مکان فعلی است. با این حساب برای مربع همسایه‌‌‌‌ی نقطه‌‌‌‌ی A ، این مقدار برابر ۱ خواهد بود و هرچقدر که از نقطه‌‌‌‌ی آغازِ حرکت دورتر شویم، مقدار G افزایش خواهد یافت.

H

تخمین ما از فاصله‌‌‌‌ی مربعی که اکنون در آن قرار داریم تا نقطه‌‌‌‌ی پایان مسیر (که از این پس آن را نقطه‌ی B می‏‌نامیم) است. این عدد لزوماً مقدار واقعی نیست چون ما هنوز مسیر را نپیموده‌‌‌‌ایم تا مقداد دقیق آن را بفهمیم بلکه فقط یک حدس است.

شاید بپرسید که منظور از ‌هزینه‌‌‌‌‌ی حرکت (Movement Cost) چیست؟ خوب، در این بازی ما بسیار ساده است – صرفاً تعداد مربع‌‌‌‌هایی است که از روی آن‌‌‌‌ها عبور کرده‌‏ایم.

به هر حال باید به یاد داشته باشید که نحوه‌‌‌‌ی محاسبه‌‌‌‌ی G و H متناسب با شرایط بازی می‌‌‌‌تواند تغییر کند. مثلاً:

• اگر شما مجاز به حرکت‌‌‌‌های قطری (اُریب) باشید، باید ‌هزینه‌‌‌‌‌ی حرکت مربوط به حرکت‌‌‌‌های قطری را اندکی بیشتر از حرکت‌‌‌‌های مستقیم (بالا، چپ، پایین و راست) در نظر بگیرید.
• اگر در بازی شما عوارض و موانع طبیعی مختلفی وجود دارد باید ‌هزینه‌‌‌‌‌ی حرکت را برای عبور از باتلاق، دریاچه و هر مانعی که عبور از آن مشکل‌‌‌‌تر است، بیشتر در نظر بگیرید.

این‌‌‌‌ها همگی مفاهیم کلّی بودند – حالا وقت دقیق شدن در جزئیات محاسبه‌‌‌‌ی G و H است.

درباره‌‌‌‌ی G بیشتر بدانید

به یاد بیاورید که G ‌هزینه‌‌‌‌‌ی حرکت (و به طور خاص در بازی ما، تعداد مربع‌‌‌‌های پیموده شده) از نقطه‌‌‌‌ی شروع حرکت یعنی A تا موقعیت کنونی است.

برای محاسبه‌‌‌‌ی G در یک مکان خاص از مسیر، ما باید G مربوط به موقعیتِ والد (Parent) آن (یعنی آخرین مربعی که از آن گذشته‌‌‌‌ایم و به اینجا رسیده‌‌‌‌ایم) را در نظر بگیریم و یک واحد به آن اضافه کنیم. با این دستورالعمل، G مربوط به هر مربع، تعداد مربع‌‌‌‌هایی است که از نقطه‌‌‌‌ی شروع یعنی A تا موقعیت کنونی از روی آن‌‌‌‌ها عبور کرده‌‌‌‌ایم.

به عنوان مثال، نمودار زیرین دو مسیر متفاوت را به سوی دو تکه استخوان متفاوت نشان می‌‌‌‌دهد که مقادیر G مربوط به هر مربع موجود در مسیر روی خود آن مربع نوشته شده است:

درباره‌‌‌‌ی H بیشتر بدانید

به یاد بیاورید که H ‌هزینه‌‌‌‌‌ی حرکت تخمینی (یعنی تعداد مربع‌‌‌‌های باقیمانده) از موقعیت فعلی تا نقطه‌‌‌‌ی پایان مسیر یعنی B است.

هر چقدر که ‌هزینه‌‌‌‌‌ی حرکت تخمینی به اندازه‌‌‌‌ی واقعی نزدیک‌‌‌‌تر باشد، مسیر نهایی درست‌‌‌‌تر خواهد بود. اگر این مقدار تخمینی مورد استفاده قرار نگیرد، ممکن است مسیر نهایی کوتاه‌‌‌‌ترین مسیر نباشد (البته شاید نزدیک به آن باشد). این موضوع بسیار پیچیده است و از این رو در این مقاله پوشش داده نخواهد شد.

برای این که کارمان را ساده کنیم از روش فاصله‌‌‌‌ی منهتن (Manhattan distance method) که با نام‌‌‌‌های طول منهتن (Manhattan Length) یا فاصله‌‌‌‌ی بلوک شهری (City block distance) هم شناخته می‌‌‌‌شود استفاده می‌‌‌‌کنیم. در این روش بدون در نظر گرفتن موانع و عوارض طبیعی موجود در مسیر، فقط فاصله‌‌‌‌ی افقی و عمودی از نقطه‌‌‌‌ی فعلی تا رسیدن به نقطه‌‌‌‌ی نهایی یعنی B را در نظر می‏‌گیریم.

به عنوان مثال، تصویر زیر چگونگی استفاده از «فاصله‌‌‌‌ی بلوکی» را در محاسبه‌‌‌‌ی H نشان می‌‌‌‌دهد (که مقدار آن با رنگ سیاه در مربع مربوطه نوشته شده است):

الگوریتم آ-ستاره

حالا که متوجه شدید چگونه باید امتیاز هر مربع را محاسبه کنیم (که از این به بعد آن را F می‌‌‌‌نامیم و برابر با G+H است)، وقت آن است که ببینیم الگوریتم آ-ستاره چگونه کار می‌‌‌‌کند.

گربه‌‌‌‌ی ما کوتاه‌‌‌‌ترین مسیر را با تکرار کردن مراحل زیر پیدا خواهد کرد:

1. مربعی که کم‌‌‌‌ترین امتیاز را در لیست باز دارد را در نظر می‌‌‌‌گیریم. از این پس این مربع را S می‌‌‌‌نامیم.
2. S را از لیست باز حذف می‌‌‌‌کنیم و به لیست بسته اضافه می‌‌‌‌کنیم.
3. به ازای هر مربعِ T که در همسایگی S قرار دارد:
4. اگر T در لیستِ بسته است: آن را نادیده بگیر. (کاری به کارش نداشته باش.)
5. اگر T در لیستِ باز نیست: آن را به لیست باز اضافه کن و امتیازش (F) را محاسبه کن.
6. اگر T در لیستِ باز است: بررسی کن که با در نظر گرفتن S به عنوان موقعیت والد و محاسبه‌‌‌‌ی مجددِ G ، آیا امتیازِ F آن کاهش می‌‌‌‌یابد؟ اگر پاسخ مثبت است، امتیاز آن را به روز کن و موقعیتِ والد آن را نیز به روز کن.

اگر هنوز هم کمی سردرگم هستید، نگران نباشید چون از این پس با یک مثال و گام به گام پیش خواهیم رفت تا نحوه‌‌‌‌ی عملکرد این الگوریتم را عیناً مشاهده کنید!

مسیر گربه

بگذارید با همان مثالِ گربه‌‌‌‌ی تنبل خودمان و مسیرش به سوی تکه استخوان پیش برویم.

در نمودارهای زیر، مقادیرِ F = G + H مطابق با نکات زیر داخل هر مربع نوشته شده‌‌‌‌اند:

F (امتیاز مربع مربوطه): گوشه‌‌‌‌ی چپ و بالا

G (مسافت پیموده شده از A تا مربع مربوطه): گوشه‌‌‌‌ی چپ و پایین

H (مسافت تخمینی از مربع مربوطه تا B): گوشه‌‌‌‌ی راست و پایین

همچنین، پیکان‌‌‌‌های موجود در هر مربع، جهت حرکتی که برای رفتن به آن مربع نیاز است را نشان می‌‌‌‌دهد.

در نهایت، در هر مرحله، مربع‌‌‌‌های سرخ‌‌‌‌رنگ نشان دهنده‌‌‌‌ی موارد موجود در لیست بسته هستند و مربع‌‌‌‌های سبزرنگ نشان دهنده‌‌‌‌ی موارد موجود در لیست باز هستند.

بسیار خوب، حالا شروع می‌‌‌‌کنیم:

گام اوّل

در گام اوّل، گربه‌‌‌‌ی ما از میان مربع‌‌‌‌های مجاورِ مکان کنونی یعنی A ، مربع‌‌‌‌هایی را که مسدود نیستند شناسایی کرده و امتیازِ F آن‌‌‌‌ها را محاسبه می‌‌‌‌کند و سپس آن‌‌‌‌ها را به لیست باز اضافه می‌‌‌‌کند:

در شکل بالا می‏‌ببینید که مقدار H برای هر مربع نوشته شده است (دو تا از آن‌‌‌‌ها ۶ هستند و یکی ۴). من پیشنهاد می‌‌‌‌کنم که از همان روش شمارش مربع‌‌‌‌ها با توجه به «فاصله‌‌‌‌ی بلوکی» استفاده کنید تا متوجه شوید که چگونه H را محاسبه کرده‏ایم.

همچنین توجه داشته باشید که مقدارِ F (در گوشه‌‌‌‌ی چپ و بالا) صرفاً حاصل جمع G+H است (که در گوشه‌‌‌‌های پایینی نوشته شده‌‌‌‌اند.)

گام دوم

در گام بعدی، گربه‌‌‌‌ی ما مربعی که کم‌‌‌‌ترین مقدار F را دارد، انتخاب کرده و آن را به لیست بسته اضافه می‌‌‌‌کند، از لیست باز حذف می‌‌‌‌کند و مربع‌‌‌‌های مجاور این مربع جدید (که کم‌‌‌‌ترین F را داشته است) را شناسایی می‌‌‌‌کند.

مربعی که کمترین امتیاز را دارد همان مربعی است که مقدارِ F آن برابر ۵ است. گربه تلاش می‌‌‌‌کند که تمام مربع‌‌‌‌های مجاور را به لیستِ باز اضافه کند (و امتیاز آن‌‌‌‌ها را محاسبه کند)، اما باید توجه داشته باشید که او نمی‌‌‌‌تواند مکان قبلی خودش را (که هم اکنون در لیستِ بسته قرار دارد) یا موانع موجود در مسیر مانند مربع‌‌‌‌های هاشور خورده را (که قابل تردد نیستند) به لیست باز اضافه کند.

توجه کنید که برای مربع‌‌‌‌های جدیدی که به لیست باز افزوده می‌‌‌‌شوند، مقدارِ G به اندازه‌‌‌‌ی یک واحد افزایش پیدا می‌‌‌‌کند چون این مربع‌‌‌‌ها به اندازه‏ی ۲ کاشی با نقطه‌‌‌‌ی شروع فاصله دارند. برای اطمینان از مقدار H هم می‌‌‌‌توانید از شمارش «فاصله‌‌‌‌ی بلوکی» استفاده کنید.

گام سوم

دوباره مربعی که کمترین مقدار F (یعنی ۵) را داراست انتخاب کرده و روند پیشین را تکرار می‌‌‌‌کنیم:

در این مرحله تنها یک کاشی می‌‌‌‌تواند به لیست باز اضافه شود، چون دوتا از کاشی‌‌‌‌های همسایه مسدود هستند و یکی هم در لیستِ بسته قرار دارد.

گام چهارم

حالا با یک وضعیت جالب مواجه شده‌‌‌‌ایم. همان‌‌‌‌گونه که در گام سوم مشاهده کردید، ۴ مربع با مقدارِ F یکسان (یعنی ۷) موجودند؛ الآن چه باید کرد؟!

راه حل‌‌‌‌های مختلفی برای این وضعیت وجود دارد اما ساده‌‌‌‌ترین و در عین حال سریع‌‌‌‌ترین راه این است که آخرین مربعی که به لیستِ باز اضافه شده است را برای حرکت بعدی انتخاب کنیم:

این بار دو کاشی قابل تردد در همسایگی وجود دارند که امتیاز آن‌‌‌‌ها را حساب می‌‌‌‌کنیم.

گام پنجم

دوباره مربعی که کمترین مقدار F (یعنی ۷) را داراست و آخر از همه به لیستِ باز افزوده شده است انتخاب می‌‌‌‌کنیم:

در این مرحله فقط یک مربعِ قابلِ تردد به لیست باز اضافه می‌‌‌‌شود. کم کم به استخوان نزدیک می‌‌‌‌شویم!

گام ششم

دیگر خودتان روند کار را یاد گرفته‌‌‌‌اید! مطمئنم که می‌‌‌‌توانید گام بعدی را حدس بزنید:

تقریباً رسیده‌‌‌‌ایم، امّا این بار مشاهده می‌‌‌‌کنید که دو مسیر وجود دارد که هر دو طول یکسانی دارند و کوتاه‌‌‌‌ترین مسیر هستند.  می‌‌‌‌توانیم یکی از آن‌‌‌‌ها را انتخاب کنیم تا به استخوان برسیم:

در مثال ما ۲ مسیر مختلف به عنوان کوتاه‌‌‌‌ترین مسیر وجود دارند:

۶ – ۵ – ۴ – ۳ – ۲ – ۱

۷ – ۵ – ۴ – ۳ – ۲ – ۱

فرقی نمی‌‌‌‌کند که کدام‌‌‌‌یک از آن‌‌‌‌ها را انتخاب کنیم، این موضوع باید در پیاده‌سازی الگوریتم هنگام کدنویسی در نظر گرفته شود.

گام هفتم

بگذارید مسیر را از طریق یکی از این دو مربع ادامه دهیم:

حالا استخوان در لیستِ باز است!

گام هشتم

در وضعیتی که استخوان (نقطه‌‌‌‌ی مقصد) در لیست باز قرار گیرد، الگوریتم آن را به لیستِ بسته اضافه می‌‌‌‌کند:

سپس تنها کاری که الگوریتم باید انجام دهد این است به عقب برگردد و مسیر نهایی را شناسایی کند.

یک گربه‌‌‌‌ی معمولی

در مثال فوق، ما می‌‌‌‌بینیم که وقتی گربه به دنبال کوتاه‌‌‌‌ترین مسیر می‌‌‌‌گشت، غالباً بهترین مربع را انتخاب می‌‌‌‌کرد (آن مربعی که در راستای کوتاه‌‌‌‌ترین مسیرِ آینده‌‌‌‌اش قرار داشت) – گویا گربه‌‌‌‌ی ما می‏‌توانست آینده را پیش‏بینی کند.

اما چه می‌‌‌‌شد اگر گربه‌‌‌‌ی ما نمی‌‌‌‌توانست آینده را ببیند و همواره اوّلین مربعی را که به لیست اضافه می‌‌‌‌شد انتخاب می‌‌‌‌کرد؟

شکل زیر نشان می‌‌‌‌دهد که اگر چنین فرایندی را طی می‌‌‌‌کردیم باید چه مربع‌‌‌‌هایی را مورد بررسی قرار می‌‌‌‌دادیم. شما مشاهده می‌‌‌‌کنید که در این حالت گربه‌‌‌‌ی ما مربع‌‌‌‌های بیشتری را امتحان می‌‌‌‌کند، امّا باز هم کوتاه‌‌‌‌ترین مسیر را پیدا می‌‌‌‌کند (نه دقیقاً همان مسیری که قبلاً پیدا کرده بود امّا مسیر دیگری با طول یکسان پیدا می‌‌‌‌کند):

مربع‌‌‌‌های سرخ‌‌‌‌رنگ در نمودار فوق لزوماً کوتاه‌‌‌‌ترین مسیر را نشان نمی‌‌‌‌دهند، آن‌‌‌‌ها فقط مربع‌‌‌‌هایی را نشان می‌‌‌‌دهند که در مراحل مختلف به عنوانِ مربعِ S در نظر گرفته شده‌‌‌‌اند.

من توصیه می‌‌‌‌کنم که به نمودار بالایی نگاه کنید و سعی کنید که همگام با آن پیش بروید. این بار در هر چندراهی، «بدترین» مسیر را برای رفتن انتخاب کنید. خواهید دید که باز هم با پیمودن کوتاه‌‌‌‌ترین مسیر به انتها می‌‌‌‌رسید!

شما می‌‌‌‌بینید که اگر مربعِ «اشتباه» را دنبال کنید، مشکلی پیش نمی‌‌‌‌آید و شما با کوتاه‌‌‌‌ترین مسیر به انتها می‌‌‌‌رسید هرچند که باید روند الگوریتم را بیشتر تکرار کنید.

در هنگام اجرای الگوریتم، مربع‌‌‌‌ها را با توجه به الگوریتم زیر به لیستِ باز اضافه می‌‌‌‌کنیم:

مربع‌‌‌‌های همسایه به این ترتیب در نظر گرفته می‌‌‌‌شوند:

بالا / چپ / پایین / راست (البته شما می‌توانید ترتیب دیگری انتخاب کنید!)

یک مربع پس از تمام مربع‌‌‌‌هایی که امتیاز یکسانی با آن دارند به لیستِ باز افزوده می‌‌‌‌شود (بنابر این اوّلین مربعی که اضافه می‌‌‌‌شود اولّین مربعی است که گربه انتخاب می‌‌‌‌کند).

این یک نمودار برای عقب‌‌‌‌گرد و بازخوانی مسیر است:

کوتاه‌‌‌‌ترین مسیر با شروع از نقطه‌‌‌‌ی مقصد و عقب رفتن از یک مربع والد به مربع والد دیگر ساخته می‌‌‌‌شود (مثلاً: در مربعِ مقصد می‌‌‌‌بینیم که پیکانِ داخلِ آن به سمت راست است پس مربعِ والد آن در سمت چپ قرار دارد).

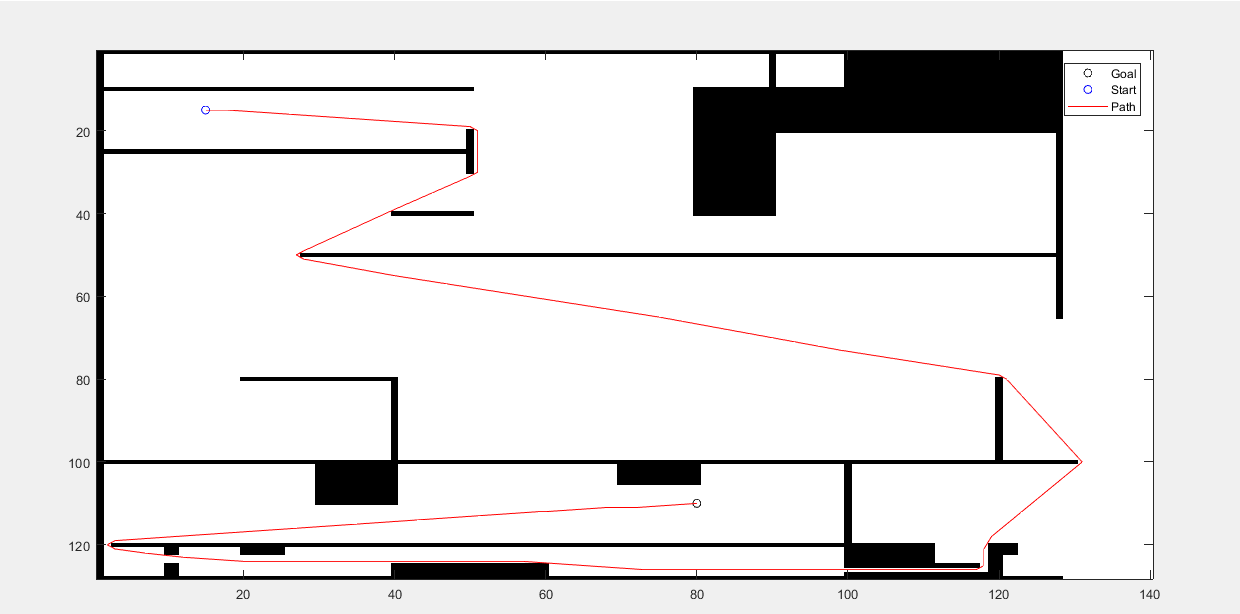
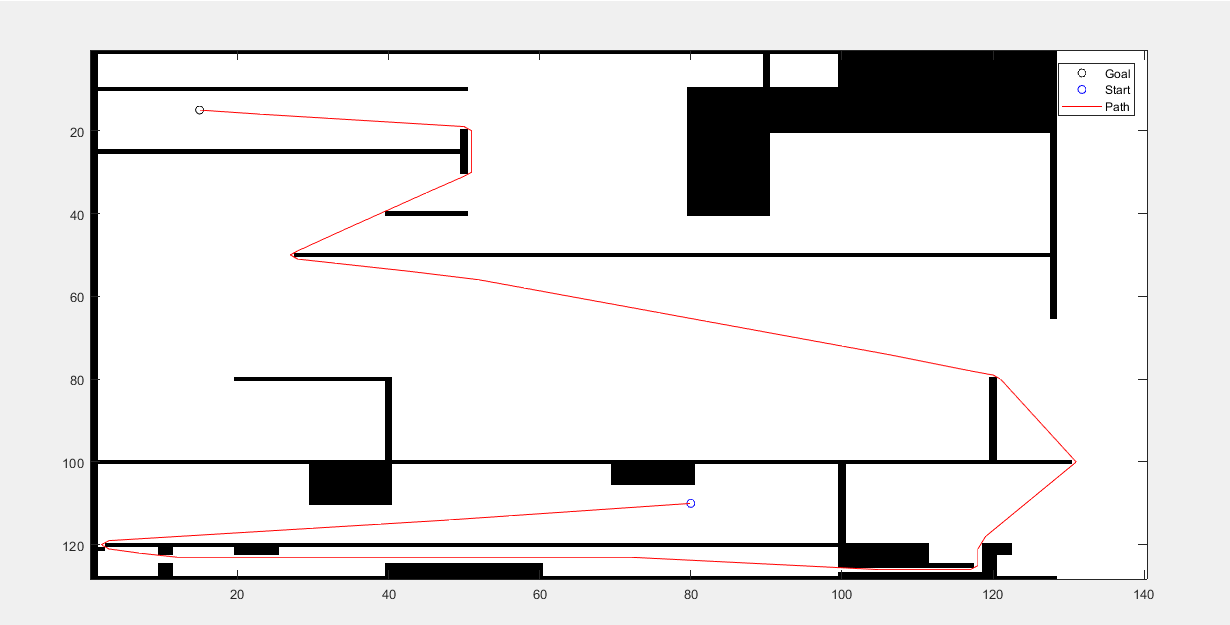
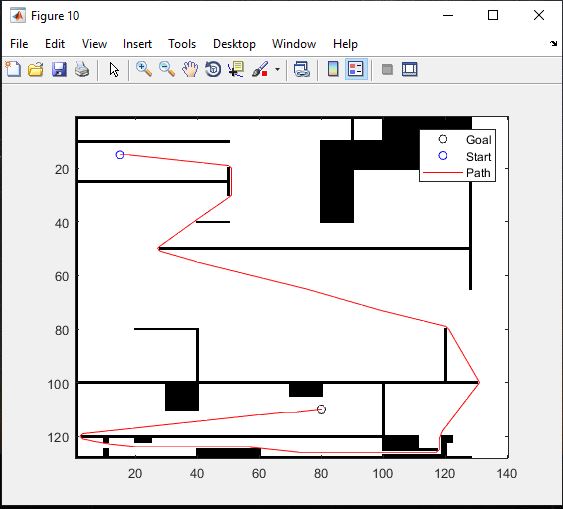
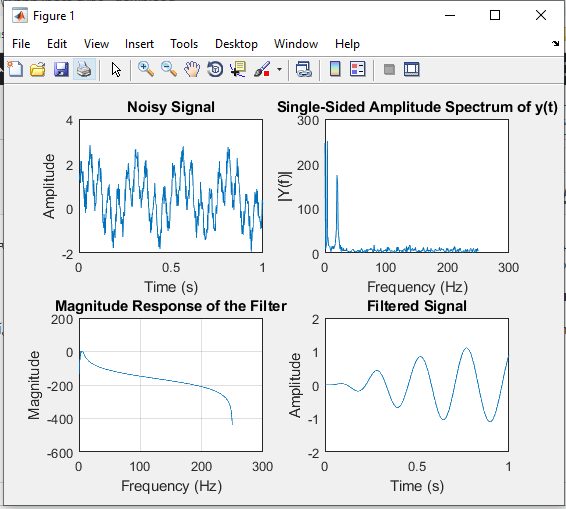
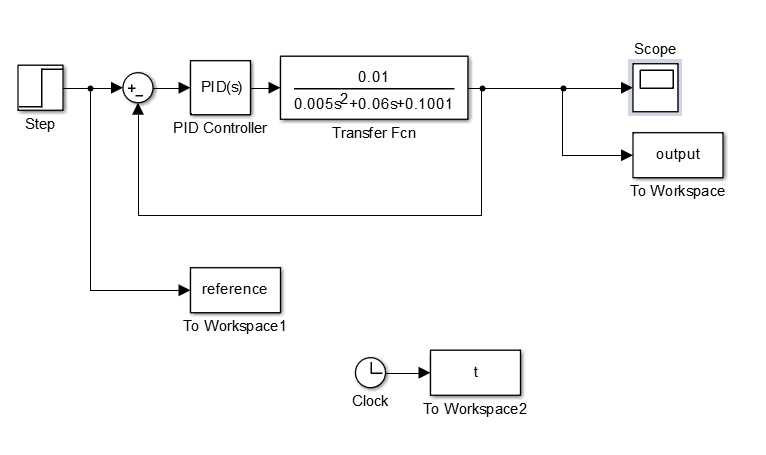
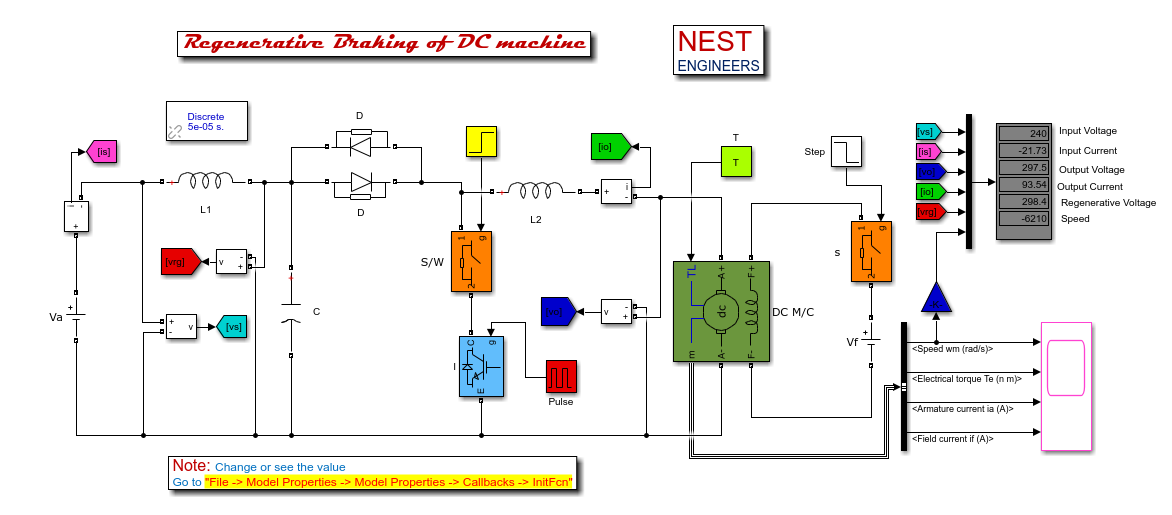
خروجی متلب :