پروژه کنترل بهینه مقطع ارشد با گزارش فارسی کامل
پروژه کنترل بهینه مقطع ارشد با گزارش فارسی کامل: پروژه آماده متلب
کنترل بهینه
پروژه آماده متلب: کنترل بهینه (انگلیسی: Optimal control) بسطی از حسابان تغییرات و یک روش بهینهسازی ریاضی برای به دست آوردن قوانین کنترلی است. این شیوه به طور عمده ناشی از کار لو پونتریاگین و همکارانش در اتحاد شوروی و ریچارد بلمن در آمریکا است.
روش عمومی
پروژه آماده متلب: موضوع کنترل بهینه مسئلهٔ یافتن یک قانون کنترلی برای سیستم داده شده به نحوی است که معیار بهینگی معینی حاصل شود. یک مسئلهٔ کنترلی دارای تابع هزینه است که تابعی است که تابعی از متغیرهای حالت و کنترلی است. یک کنترل بهینه یک مجموعه معادله دیفرانسیل است که مسیرهای متغیرهای کنترلی را توصیف میکند که تابع هدف را بهینه کنند. کنترل بهینه را میتوان از اصل ماکسیمم پونتریاگین به دست آورد.
تابع هدف پیوسته در زمان باید مینیمم شود:
- {\displaystyle J=\Phi \,[\,{\textbf {x}}(t_{0}),t_{0},{\textbf {x}}(t_{f}),t_{f}\,]+\int _{t_{0}}^{t_{f}}{\mathcal {L}}\,[\,{\textbf {x}}(t),{\textbf {u}}(t),t\,]\,\operatorname {d} t}
مقید به شرطهای دینامیک درجه اول:
- {\displaystyle {\dot {\textbf {x}}}(t)={\textbf {a}}\,[\,{\textbf {x}}(t),{\textbf {u}}(t),t\,],}
شرطهای مسیر جبری
- {\displaystyle {\textbf {b}}\,[\,{\textbf {x}}(t),{\textbf {u}}(t),t\,]\leq {\textbf {0}},}
و شرطهای مرزی
- {\displaystyle {\boldsymbol {\phi }}\,[\,{\textbf {x}}(t_{0}),t_{0},{\textbf {x}}(t_{f}),t_{f}\,]=0}
پروژه آماده متلب: که در آن {\displaystyle {\textbf {x}}(t)} متغیر حالت, {\displaystyle {\textbf {u}}(t)} متغیر کنترل, {\displaystyle t} متغیر مستقل (معمولاً زمان), {\displaystyle t_{0}} زمان اولیه و {\displaystyle t_{f}} زمان پایانی است
.
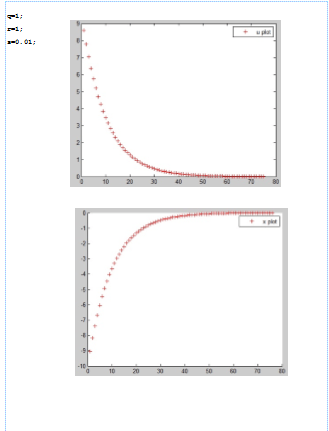
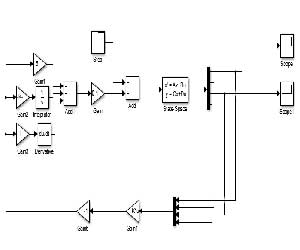
خروجی های متلب:

![{\displaystyle J=\Phi \,[\,{\textbf {x}}(t_{0}),t_{0},{\textbf {x}}(t_{f}),t_{f}\,]+\int _{t_{0}}^{t_{f}}{\mathcal {L}}\,[\,{\textbf {x}}(t),{\textbf {u}}(t),t\,]\,\operatorname {d} t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b888b432e8bef70b322a14309e6bd29bec7bc4bf)
![{\displaystyle {\dot {\textbf {x}}}(t)={\textbf {a}}\,[\,{\textbf {x}}(t),{\textbf {u}}(t),t\,],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d4f9f2e6f7414f1c81d408ced956508a5f9ea65)
![{\displaystyle {\textbf {b}}\,[\,{\textbf {x}}(t),{\textbf {u}}(t),t\,]\leq {\textbf {0}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68da65cbeb1dc4bbeb077b63a45f6a3a451acb98)
![{\displaystyle {\boldsymbol {\phi }}\,[\,{\textbf {x}}(t_{0}),t_{0},{\textbf {x}}(t_{f}),t_{f}\,]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1797c5eddb15c0c730d0f8ea3d907fd1449e3cad)






لطفاً براي ارسال دیدگاه، ابتدا وارد حساب كاربري خود بشويد