حل معادلات دیفرانسیل با متلب (رابط gui) :انجام پروژه متلب
حل معادلات دیفرانسیل با متلب (رابط gui) همراه داکیومنت لاتین :انجام پروژه متلب
انجام پروژه متلب:در این پروژه حل معادلات در نرم افزار انجام میشود و فقط نمودار خروجی رو میتوانیم ببینیم بصورت نموداری و برنامه در دانشگاه اوهایو امریکا نوشته شده است و همراه راهنمای فارسی می باشد.
معادلات دیفرانسیل معمولی (ODE) به آن دسته از معادلات دیفرانسیل گفته میشود که توابع مجهول در آنها بر حسب تنها یک متغیر مستقل باشد. معادله‌ای که بیشتر از یک متغیر مستقل داشته باشد را معادله دیفرانسیل نسبی یا معادله دیفرانسیل با مشتقات جزئی (PDE) پروژه متلب می‌نامند.
حل معادلات دیفرانسیلی سخت و غیرسخت
بسته به نوع معادلات که اصطلاحا به آنها سخت (stiff) و غیرسخت (stiffness) گفته می شود، روش حل آنها در MATLAB کمی متفاوت خواهد بود. اصطلاح سخت (stiff) برای آن دسته از معادلاتی بکار می رود که برای مثال در مقابل متغیر مستقلی همچون t چند متغیر وابسته مانند x و y و… وجود دارد، بگونه ای که اندازه مشتقات متغیرهای وابسته نسبت به متغیر مستقل بطور قابل ملاحظه ای متفاوت است. در غیر اینصورت معادله غیرسخت نامیده می شود. همچنین معادلات سخت شامل آن دسته از معادلات دیفرانسیلی می شوند که حل آنها با روش محاسبات عددی پایدار و همگرا نبوده و تنها راه حل آنها، بسیار کوچک کردن گام (Step) در روش عددی می باشد. اگر در معادله دیفرانسیلی، متغری وجود دارد که باعث تغییرات بسیار زیاد در جواب مساله می شود، این دسته را جز معادلات غیرسخت طبقه بندی می کنند.
| کاربرد | دقت | نوع مساله | دستور |
| اکثر موارد (سعی شود جهت حل معادله ابتدا از این دستور استفاده شود) | متوسط | غیرسخت | ode45 |
| حل مسائل دارای خطای خام (crude error)، حل مسائل تقریبا سخت | پایین | غیرسخت | ode23 |
| حل مساله دارای خطای دقیق، معادلات مربوط به محاسبات عددی زمان بر | پایین تا بالا | غیرسخت | ode113 |
| هنگامی که حل معادله با دستور ode45 بسیار کند پیش رود. | پایین تا متوسط | سخت | ode15s |
| مسائل دارای خطای خام (crude error) ، هنگامی که ماتریس جرم (mass matrix) ثابت باشد | پایین | سخت | ode23s |
| حل معادلات بدون میرایی عددی (numerical damping) | پایین | سخت | ode23t |
| حل مساله با خطای خام و معادله سخت | پایین | سخت | ode23tb |
مثال) حل معادله زیر با دستور ode45
گام اول: بازنویسی مسئله بشکل مجموعه ای از معادلات مرتبه یک. با تغییر متغیر y۱‘=y۲ دو معادله دیفرانسیل مرتبه یک حاصل میشود:
گام دوم: استفاده از ODE های مرتبه یک،:انجام پروژه متلب پس از بازنویسی معادلات مطابق گام اول، باید ان معادلات را برای بکارگیری ode45 کد نماییم:
توجه نمایید که تابع باید دارای دو آرگومان باشد؛ یکی مربوط به متغیر مستقل (t) و دیگری مربوط به متغیرهای وابسته (y). حتی اگر هیچکدام در تابع های مرتبه یک ظاهر نشوند، باید آن را لحاظ نمود:
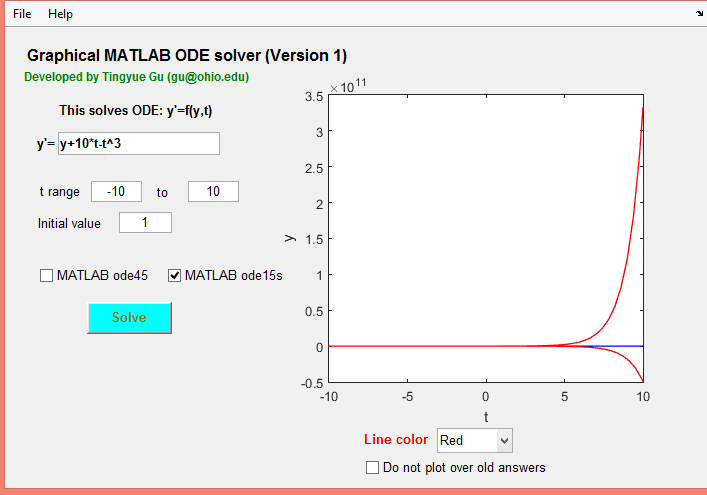
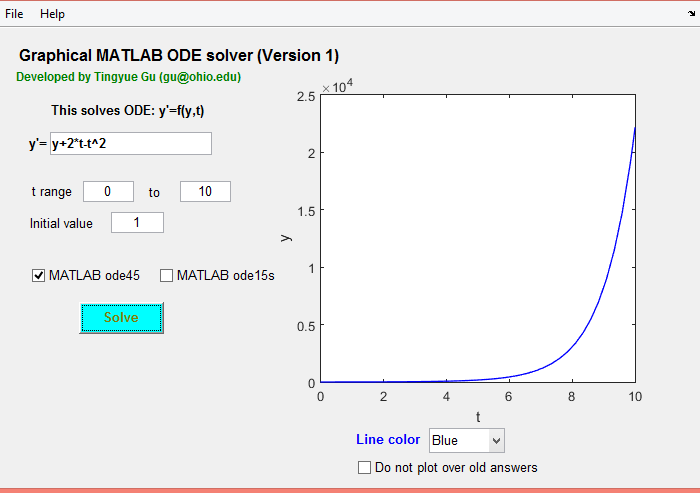
حل، معادلات دیفرانسیل،متلب ،رابط gui،انجام پروژه متلب
انجام پروژه متلب
دیدگاه ها