تشخیص کف دست با الگوریتم ورونی در متلب - انجام پروژه متلب |پروژه متلب | انجام پروژه متلب برق | شبیه سازی با متلب

تشخیص کف دست با الگوریتم ورونی در متلب

تشخیص کف دست با الگوریتم ورونی در متلب :پروژه متلب

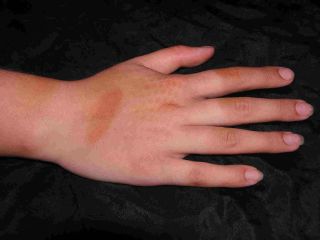
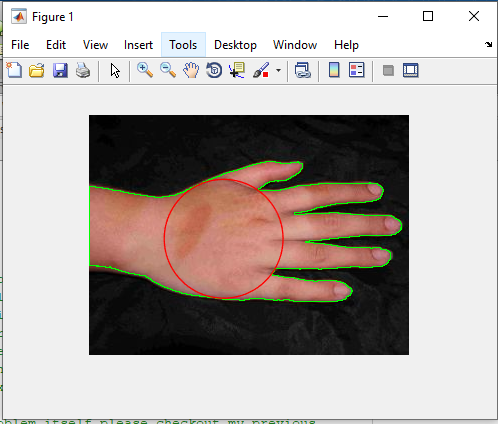
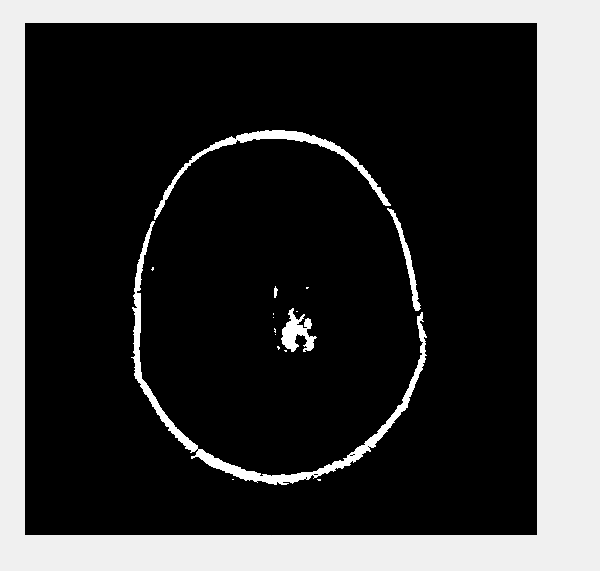
پروژه متلب  در این پروژه با کمک الگوریتم ورونی کف دست شناسایی و سپس سگمنت گذاری و جداسازی می گردد.

پروژه متلب  : در علم ریاضیات دیاگرام ورونوی روشی برای تقسیم فضا به تعدادی ناحیه می‌باشد. در این دیاگرام به هر مجموعه‌ای از نقاط (که دامنه‌ها، سایت‌ها یا ژنراتورها نامیده می‌شوند) ناحیه‌ای اختصاص داده می‌شود. این نواحی سلول‌های ورونوی نامیده می‌شود. برای یک مجموعه از نقاط دیاگرام ورونوی سطح را به مناطقی تقسیم‌بندی می‌کند که برای هر نقطه از مجموعه نقاط یک منطقه تعریف می‌شود. به طوری که تمام نقاط این منطقه به نقطه تولیدکننده آن منطقه نزدیکتر می‌باشد. از کاربردهای این دیاگرام در مثلث بندی دیلانی می‌باشد.

این دیاگرام به افتخار یوهان پتر گوستاف لوژون دیریکله به نام موزاییک کاری دیریکله، و بعد از گریگوری وُرنوی به نام موزاییک کاری وُرُنوی یا تجزیه وُرُنوی نامیده شد. دیاگرام‌های ورونوی در علوم و فناوری‌های متعدد یا حتی در هنر کاربرد دارد و تاکنون کاربردهای متفاوتی از آن در زمینه‌های خاص گزارش شده‌است.

به عنوان یک توضیح ساده، مجموعه از فروشگاه‌ها را در یک شهر مسطح در نظر می‌گیریم. فرض کنید که می‌توان تعداد مشتریان فروشگاه را تخمین زد. در نظر می‌گیریم سایر پارامترها (مانند قیمت‌ها، محصولات، کیفیت خدمات و…)ثابت باشد. به طوریکه تنها فاکتور انتخاب فروشگاه توسط مشتریان فاصله تا فروشگاه باشد. بنابراین مشتریان فروشگاهی را انتخاب می‌کنند که از موقعیت آن‌ها حداقل فاصله را داشته باشد. در اینجا سلول ورونوی {\displaystyle \displaystyle {R_{k}}} و فروشگاه{\displaystyle \displaystyle {P_{k}}} بوده و از نمودار ورونوی می‌توان برای تخمین تعداد مشتریان فروشگاه استفاده نمود (در مدلسازی ما هر فروشگاه در شهر در حقیقت یک نقطه دیاگرام ورونوی می‌باشد.) تا به اینجا فرض بر این بوده که فاصله بین نقاط در شهر به صورت استاندارد اندازه گیری شده‌است که متناظر با فضای اقلیدسی است به طوریکه {\displaystyle d((a_{1},a_{2}),(b_{1},b_{2}))={\sqrt {(a_{1}-b_{1})^{2}+(a_{2}-b_{2})^{2}}}}.
پروژه متلب به هر حال اگر ما مسئله را طوری بررسی کنیم که مشتریان تنها با وسیله نقلیه به فروشگاه رفته و مسیرهای ترافیکی به موازات محورهایX و Y باشد، مانند جزیره منهتن، بنابراین تابع فاصله واقعی فاصله {\displaystyle \ell _{1}} خواهد بود که آن را {\displaystyle d} می‌نامیم به طوری که {\displaystyle \displaystyle {d((a_{1},a_{2}),(b_{1},b_{2}))=|a_{1}-b_{1}|+|a_{2}-b_{2}|}}.

ماهیت 

• پروژه متلب گراف دو تایی برای دیاگرام ورونوی (در مورد فضای اقلیدسی با سایت‌های نقطه‌ای) مشابه مثلث بندی دلانی برای همان مجموعه نقاط می‌باشد.
• نزدیکترین جفت نقاط متعلق به دو سلول مجاور در دیاگرام ورونوی می‌باشد.
• فرض کنید که مجموعه‌ای از نقاط در فضای اقلیدسی داده شده باشد. بنابراین دو نقطه مجاور در پوش محدب وجود دارند اگر و تنها اگر سلول‌های ورونوی آن‌ها در یک جهت طولانی نامتناهی مشترک باشند.
• اگر فضای مورد مطالعه یک فضای هنجار و فاصله هر سایت قابل دسترسی باشد (به عنوان مثال هنگامی که یک سایت یک مجموعه فشرده یا توپ محصور شده باشد) پس هر سلول ورونوی می‌تواند به عنوان اجتماعی از قطعات خطی ناشی از سایت‌ها نمایش داده شود.As همان‌طور که نشان داده شده‌است زمانی که فاصله تعیین نشده باشد لزوماً ماهیت نمودار حفظ نمی‌شود.
• تحت شرایط عمومی نسبی (فضای مورد مطالعه فضایی واحد و محدب و به احتمال زیاد دارای بعد نامحدود بوده و در نتیجه تعداد بسیار نامحدودی سایت در حالت عمومی وجود دارد.)سلول‌های ورونوی دارای ماهیت پایدار معین خواهند بود: تغییر کوچکی در شکل سایت‌ها، به عنوان مثال ایجاد تغییر توسط انتقال یا تحریف، منجر به تغییر شکل سلول‌های ورونوی می‌شود که این عمر به دلیل پایدار هندسی دیاگرام ورونوی می‌باشد.. همان‌طور که در این جا نشان داده شده‌است در حالت عمومی ماهیت ثابت نخواهد ماند حتی اگر فضا دو بعدی (اما در شرایط محدب غیر یکنواخت و در حالت خاص غیر اقلیدسی) و سایت‌ها نقطه‌ها باشند.

تاریخچه و تحقیقات 

پروژه متلب استفاده غیر رسمی از دیاگرام ورونوی به سال ۱۶۴۴ و توسط دکارت بر می‌گردد.یوهان پتر گوستاف لوژون دیریکله از نمودارهای ورونوی دو و سه بعدی در مطالعات فرم و حالت درجه دو در سال ۱۸۵۰ استفاده کرد. فیزیکدان انگلیسی به نام جان اسنو در سال ۱۸۵۴ از یک نمودار ورونوی استفاده کرد تا بتواند پاسخ مناسبی برای این سؤال پیدا کند که چگونه اکثریت مردم ساکن سوهو که در اثر ابتلا به بیماری وبا جان خود را از دست می‌دهند در نزدیکی پمپ‌های «خیابان ِ برود» زندگی می‌کنند که آلوده به عامل عفونت وبا می‌باشد در صورتی که اقلیت مبتلایان از سایر پمپ‌های آب استفاده می‌نمودند.

پروژه متلب دیاگرام ورونوی بعد از ریاضیدان اوکراینی گریگُری ورونوی با این نام شناخته شد. ورونوی در سال ۱۹۰۸ مطالعات خود را بر این دیاگرام در فضای {\displaystyle n} بعدی عمومی انجام داد. دیاگرام ورونوی مورد استفاده در ژئوفیزیک و هواشناسی به منظور آنالیز داده‌های توزیع فضایی (مانند اندازه‌گیری میزان بارش)، بعد از هواشناس آمریکایی Alfredh. Thiessen با نام چند ضلعی Thiessen شناخته شد. در فیزیک مواد متراکم و فشرده مانند موزاییک کاری‌ها به عنوان سلول واحد Wigner-Seitz شناخته می‌شود.موزاییک کاری ورونوی در تکانه شبکه دو طرفه با نام مناطق Brillouin شناخته می‌شود. برای شبکه‌های عمومی در گروه لی این سلول‌ها به صورت ساده با عنوان دامنه اساسی نامیده می‌شوند. در زمینه فضاهای متریک عمومی سلول‌ها غالباً چندضلعی اساسی متریک نامیده می‌شود. سایر نام‌های معادل برای این مفهوم (و یا موارد مهم خاص آن) عبارتند از: چندوجهی ورونوی، چند ضلعی ورونوی، دامنه (های) نفوذ، تجزیه ورونوی، موزاییک کاری (های) ورونوی، موزاییک کاری‌های دیریکله.

نمونه‌ها 

موزاییک کاری شبکه‌های منظم در دو یا سه بعد در بسیاری از موزاییک کاری‌های معروف توسعه یافته‌است.

• یک شبکه دو بعدی یک موزاییک کاری شش گوش نامرتب با چند ضلعی‌های برابر و تقارن نقاط ایجاد می‌کند. در مورد شبکه مثلثی منظم موزاییک کاری منظم خواهیم داشت. در مورد شبکه مستطیلی، شش ضلعی به مستطیل در سطر و ستون کاهش پیدا می‌کند. یک شبکه مربعی یک موزاییک کاری منظم از مربعات را ایجاد می‌کند. توجه داشته باشید که شبکه‌های مستطیلی و مربعی می‌تواند توسط سایر شبکه‌ها نیز ایجاد شوند.(به عنوان مثال شبکه تولید شده به وسیله بردارهای (۱٬۰) و (۱/۲٬۱/۲) شبکه مربعی ایجاد می‌کند.)
• یک شبکه مکعبی ساده یک شش گوش مربعی می‌دهد.
• یک شبکه شش ضلعی فشرده فضای موزاییک کاری دوازده سطحی لوزی-ذوزنقه می‌دهد.
• یک شبکه مرکز وجوه پر فضای موزاییک کاری دوازده سطحی لوزی شکل تولید می‌کند.
• یک شبکه مرکز پر یک فضای موزاییک کاری هشت وجهی کوتاه می‌دهد.
• طرح‌های موازی با شبکه‌های مثلثی مرتب که مرکزهایشان پشت سر هم قرار گرفته‌اند منشور شش وجهی ایجاد می‌کند.
• شبکه‌های شش وجهی مرکز پر یک فضای موزاییک کاری دوازده سطحی شش وجهی –لوزی می‌دهد.

برای مجموعه‌ای از نقاط (x, y) با در نظر گرفتن x در مجموعه جدا X و y در مجموعه مجزا Y به کاشی مستطیلی شکل خواهیم رسید که لزوماً نقاط در مرکز آن‌ها قرار ندارند.

دیاگرام ورونوی مرتبه بالاتر 

پروژه متلب اگرچه یک سلول ورونوی نرمال به عنوان یک مجموعه از نقاط با نزدیکترین فاصله به یک نقطه تنها در S تعریف شده‌اند، یک سلول ورونوی از مرتبه {\displaystyle n} به عنوان یک مجموعه از نقاط نامیده می‌شود که یک مجموعه خاص از {\displaystyle n} در {\displaystyle S} دارند که این {\displaystyle n} نزدیکترین همسایه به نقطه تنهای مورد نظر می‌باشد. دیاگرام ورونی از مرتبه بالاتر هم چنین فضا را طبقه بندی می‌کنند.

دیاگرام ورونوی مرتبه بالاتر می‌توانند به صورت بازگشتی تولید شوند. به منظور تولید نمودار ورونوی از مرتبه {\displaystyle n} از مجموعه Sبا دیاگرام مرتبه {\displaystyle (n-1)}ام شروع نموده و هر سلول تولید شده با {\displaystyle X=\{x_{1},x_{2},\cdots ,x_{n-1}\}} را با نمودار تولید شده روی مجموعه  {\displaystyle S-X} جایگزین می‌کنیم.

نمودار ورونوی دورترین نقطه

برای یک مجموعه {\displaystyle n} نقطه‌ای، نمودار ورونوی مرتبه {\displaystyle (n-1)} ام دیاگرام ورونوی با نام دیاگرام ورونوی دورترین نقطه شناخته می‌شود.

پروژه متلب برای یک مجموعه از نقاط {\displaystyle S=\{p_{1},p_{2},\cdots ,p_{n}\}} دیاگرام ورونوی دورترین نقطه طرح را به سلول‌هایی تقسیم می‌کند که نقطه یکسان P دورترین نقطه می‌باشد. توجه داشته باشید که نقطه P دارای سلولی در دیاگرام دورترین نقطه است اگر و تنها اگر به عنوان یک راس از پوشش محدب P باشد. بنابراین {\displaystyle H=\{h_{1},h_{2},\cdots ,p_{k}\}} را به عنوان پوشش محدب P قرار داده به طوری که هر نقطه درون {\displaystyle H} با این ویژگی که نقطه q در درون سلول مربوط به سایت {\displaystyle h_{i}} قرار گرفته‌است، دیاگرام ورونوی نقطه دور را به عنوان بخشی از طرح در سلول‌های {\displaystyle k} تعریف می‌کنیم اگر و تنها اگر فاصلهٔ {\displaystyle (q,h_{i})} بیشتر از فاصله {\displaystyle (q,p_{j})} باشد و {\displaystyle p_{j}\in S} و {\displaystyle h_{i}\neq p_{j}} و فاصله {\displaystyle (q,p)} فاصله اقلیدسی بین نقطه {\displaystyle p} و {\displaystyle q} است.

عمومیت‌ها و تغییرات 

پروژه متلب به منظور روشن شدن موضوع توسط تعریف کردن، سلول‌های ورونوی می‌تواند برای متریک‌های غیر از فاصله‌های اقلیدسی (مانند ماهالانوبیس و منهتن. به هر حال در این موارد مرزهای سلول ورونوی می‌تواند نسبت به موارد اقلیدسی پیچیده تر شود. چرا که مکان هندسی هم فاصله برای دو نقطه می‌تواند به زیر فضای هم بعد یک یا دو بعدی تقسیم شود.

یک نمودار ورونوی سنگین تابعی از زوج نقاط است که به منظور تعریف سلول ورونوی، تابع فاصله به وسیله ضرب یا جمع وزن‌های نقاط تولید شده اصلاح می‌شود. در مقابل سلول‌های ورونوی توسط فاصله‌های متریک تعریف می‌شود. در این مورد برخی از سلول‌های ورونوی ممکن است خالی باشند. یک دیاگرام توان نوعی لز دیاگرام ورونوی است که مجموعه‌ای از دایره‌ها توسط فاصله توانی تعریف می‌شوند. این دیاگرام همچنین می‌تواند به عنوان دیاگرام ورونوی سنگین معرفی شود به طوری که یک وزن، از مجموع شعاع هر دایره و توان دوم فاصله از مرکز دایره تعریف می‌شود.

دیاگرام ورونوی n نقطه در فضای d بعدی، نیازمند فضای ذخیره‌سازی {\displaystyle O(n^{\lceil d/2\rceil })} می‌باشد. بنابراین دیاگرام ورونوی اغلب برای {\displaystyle d>2} امکان‌پذیر نمی‌باشد. یک پیشنهاد دیگر استفاده از دیاگرام ورونوی تقریبی است به طوری که اگر سلول‌های ورونوی دارای مرزهای فازی باشند می‌توان از این تقریب استفاده نمود.. پیشنهاد دیگر مربوط به زمانی است که هر سایت یک دایره فازی باشد و در نتیجه سلول‌ها نیز فازی شوند.

سلول‌های ورونوی همچنین با سایر ساختارهای هندسی دیگر مانند محورهای میانی (به طوری که در قطعه بندی تصویر شناسایی ماهیت نوری و سایر کاربردهای محاسباتی دیگر مورد استفاده قرار می‌گیرد.)طرح ریزی مستقیم و نمودارهای نقطه‌ای مرتبط است.

کاربردها 

• پروژه متلب در علم بیماری‌های واگیردار دیاگرام ورونوی می‌تواند در منابع وابسته به عفونت در بیماری‌های مسری مورد استفاده قرار گیرد. یکی از موارد استفاده اولیه دیاگرام‌های ورونوی توسط John Snow در سال ۱۸۵۴ در زمان شیوع وبا در سوهو و در Broad Street می‌باشد. وی ارتباط بین نواحی روی نقشه لندن را که از پمپ‌های آبی خاص استفاده می‌نمودند و نواحی با بیش‌ترین آمار مرگ و میر به دلیل شیوع بیماری وبا را با این دیاگرام نشان داد.
• یک ساختمان داده موقعیت نقطه می‌تواند در مورد دیاگرام ورونوی به منظور پاسخگویی یه جستجوی نزدیک‌ترین همسایه ایجاد شود، در جایی که شخص بخواهد نزدیکترین شی را به نقطه مورد جستجو پیدا کند. جستجوی نزدیکترین همسایه چندین کاربرد دارد:به عنوان مثال ممکن است بخواهیم نزدیکترین بیمارستان یا اشیا مشابه را در پایگاه داده پیدا کنیم. بیش‌ترین کاربرد در رقمی سازی بردار و معمولاً در فشرده سازی داده‌ها می‌باشد.
• در هندسه دیاگرام‌های ورونوی می‌تواند به منظور یافتن بزرگترین محدوده خالی از مجموعه نقاط و همچنین در چند ضلعی محصور مورد استفاده قرار گیرد. به عنوان مثال برای تأسیس یک سوپر مارکت جدید در حداکثر فاصله از سایر سوپرمارکت‌های موجود که در یک شهر خاص قرار گرفته‌اند این دیاگرام کاربرد دارد.
• دیاگرام ورونوی و دیاگرام و دیاگرام ورونوی دورترین نقطه برای الگوریتم‌های کارا به منظور محاسبه منحنی مجموعه نقاط مورد استفاده قرار می‌گیرد.
• روش ورونوی کاربرد مؤثری در سنجش مدور بودن/گرد بودن در زمان ارزیابی مجموعه داده‌ها توسط دستگاه سنجش مختصات دارد.

در فیزیک پلیمر دیاگرام ورونوی می‌تواند در نمایش دادن حجم خالی پلیمرها مورد استفاده قرار گیرد.

• در شبکه دیاگرام‌های ورونوی می‌تواند در استخراج ظرفیت شبکه بی سیم استفاده شود.
• در علم آب و هوا‌شناسی (اقلیم شناسی)دیاگرام‌های ورونوی در محاسبه میزان بارش یک منطقه بر مبنای اندازه‌گیری مجموعه‌ای از نقاط کاربرد دارد. در زمینه این کاربرد غالباً به چندضلعی Thiessen ارجاع داده می‌شود.
• در علم بوم شناسی دیاگرام ورونوی به منظور مطالعه الگوهای رشد جنگل‌ها، تاج‌پوش جنگل و همچنین استفاده مؤثر در توسعه مدل‌های پیش گویانه آتش سوزی جنگل‌ها کاربرد دارد.
• در گرافیک کامپیوتر دیاگرام‌های ورونوی به منظور ایجاد متن‌های اثلی و ساختمانی به کار برده می‌شوند.
• در هدایت ربات‌های مستقل دیاگرام‌های ورونوی به منظور یافتن مسیرهای واضح کاربرد دارند.
• در شیمی محاسباتی سلول‌های ورونوی که توسط موقعیت هسته در مولکول تعریف می‌شوند در محاسبه بارهای اتمی مورد استفاده قرار می‌گیرند. این امر توسط روش چگالی تغییر شکل ورونوی انجام می‌پذیرد.
• در دانش مواد ساختارهای میکروپلی کریستالی در آلیاژهای فلزی توسط موزاییک کاری ورونوی نمایش داده می‌شود.
• در استخراج معدن چند ضلعی ورونوی به منظور تخمین ذخایر مواد با ارزش، مواد معدنی یا سایر منابع کاربرد دارد. در اینجا حفره‌ها و سوراخ خای اکتشافی با عنوان مجموعه نقاط چندضلعی ورونوی می‌باشد.
• دریادگیری ماشینی دیاگرام‌های ورونوی در انجام طبقه‌بندی ۱-NN کاربرد دارد

خروجی متلب :