دسته بندی داده ها در متلب با شبکه عصبی :پروژه متلب آماده - انجام پروژه متلب |پروژه متلب | انجام پروژه متلب برق | شبیه سازی با متلب

دسته بندی داده ها در متلب با شبکه عصبی :پروژه متلب آماده

دسته بندی داده ها در متلب با شبکه عصبی :پروژه متلب آماده

دسته اول: اعداد صحیح

پروژه متلب آماده  اعداد صحیح در متلب دقیقا همان تعریفی را دارد که در ریاضی هم از اعداد صحیح سراغ داریم. اعدادی که اعشاری پس از خود ندارند. این اعداد در متلب با int مشخص می شوند. بعد از کلمه int یک عدد می آید که تعداد حداکثر بیت های هر نوع داده را مشخص می کند. هر چه تعداد بیت ها بیشتر باشد، اعداد بزرگتری می توانند در آن نوع از داده قرار بگیرند. در جدول زیر محدوده هر نوع را مشاهده می کنید.

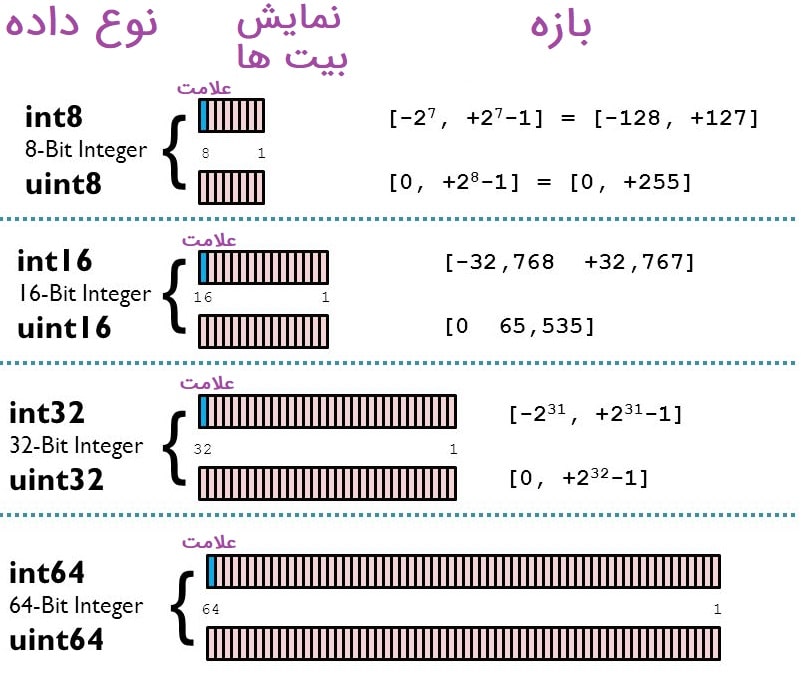
اما برای فهم بهتر به این مثال توجه کنید: فرض کنید که قصد داریم عدد ۲۴ را در متغیری به نام a ذخیره کنیم. این عدد در بازه های مربوط به همه مواردی که در جدول بالا ذکر شد وجود دارد. یعنی هم می توانیم آن را با int8 تعریف کنیم هم می توانیم با int16 و int32 و int64 تعریف کنیم. کدام بهتر است.

پاسخ را با دقت مطالعه کنید:

پروژه متلب آماده  ⇐ همانطور که می دانید کامپیوتر اعداد را در مبنای ۲ و به صورت ۰ و ۱ در حافظه خود ذخیره می کند. یعنی عدد ۲۴ به صورت ۱۱۰۰۰ ذخیره می شود و به ۵ بیت نیاز دارد. (البته یک بیت هم علامت مثبت این عدد را مشخص می کند و در نتیجه مجموعا ۶ بیت را اشغال می کند. اگر این عدد را با int16 تعریف کنیم، ۱۰ بیت، بدون دلیل اشغال می شود و در واقع اسراف می شود! که در نهایت هم باعث کندتر شدن اجرای برنامه می شود.

پس بهتر است که این عدد با int8 تعریف شود. اما چگونه باید نوع داده را مشخص کنیم؟ در ادامه آموزش به این نکته هم خواهیم رسید.

اگر به ابتدای int یک حرف u اضافه شود، uint ها به دست می آیند. این نوع داده ها، اعداد صحیح بدون علامت هستند. یعنی همگی مثبت هستند. در نتیجه بازه ای که در بین اعداد صحیح پوشش می دهند، دو برابر می شود.

مثلا int8 اعداد بین ۱۲۸- و ۱۲۷ را شامل می شود و uint8 شامل اعداد ۰ تا ۲۵۵ است. بازه تحت پوشش هر دو یکسان است. اما بازه uint تماما در بخش مثبت است و بازه int به طور مساوی بین بخش مثبت و منفی تقسیم شده است.

دسته دوم: اعداد اعشاری

پروژه متلب آماده  می توان گفت این دسته شامل همه اعداد، حتی اعداد دسته اول هم می شود. چون اعداد صحیح هم به نوعی اعداد اعشاری هستند که اعشار آنها صفر است.

این دسته از اعداد هم شامل دو شاخه می شود. شاخه اول Single نام دارد و شاخه دوم Double.پروژه متلب آماده 

دقت داده هایی که از نوع Single هستند کمتر از داده هایی است که از نوع Double هستند. اما در عوض فضای کمتری را اشغال می کنند. اعدادی که از نوع Single باشند، ۳۲ بیت (۴بایت) و اعدادی که از نوع Double باشند، ۶۴ بیت (۸بایت) را اشغال می کنند.

تعیین نوع داده عددی با استفاده از class و whos در متلب

اول از همه یک سوال مهم. در متلب وقتی یک عدد را بدون تعیین نوع آن داخل یک متغیر می ریزیم، متلب آن را چه نوع داده ای در نظر می گیرد؟

پاسخ این است که در حالت پیشفرض، عددها از نوع double هستند. برای مشخص کردن نوع یک داده، از تابع class در متلب استفاده می کنیم. مشاهده می کنید که در حالتی که نوع a مشخص نشود، نوع double برای آن در نظر گرفته می شود.

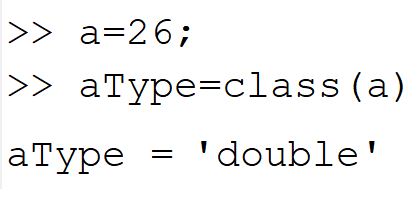
اگر اطلاعات بیشتری درباره متغیر بخواهیم، از تابع  whos در متلب استفاده می کنیم. مشاهده می کنید که در این حالت تعداد بایت ها و سایز هم نمایش داده می شود.

 

اگر بخواهیم متغیری از نوع اعداد صحیح تعریف کنیم، مطابق کد روبه رو، از کلمه int در کنار تعداد بیت های اختصاص داده شده استفاده می کنیم.

شبکه عصبی:

در سال ۱۹۰۹، «سانتیاگو رامون کاخال» (Santiago Ramon y Cajal) کشف کرد که مغز از تعداد زیادی نورون متصل به هم تشکیل شده که پیام‌های بسیار ساده تحریکی (Excitatory) و مهاری (Inhibitory) را برای یکدیگر ارسال می‌کنند و تهییج (Excitation) آن‌ها با همین پیام‌های ساده به‌روز می‌شود. یک نورون سه بخش اصلی دارد: جسم سلولی، آکسون یا آسه (Axon) که پیام‌ها را ارسال می‌کند و دندریت یا دارینه (Dendrite) که پیام‌ها را دریافت می‌کند. جسم سلولی ساختار سلول را تشکیل می‌دهد. آکسون یک رشته منشعب است که پیام‌های نورون را به بیرون منتقل می‌کند. دندریت‌ها انشعاب‌های بیشتری دارند و سیگنال سلول‌های عصبی دیگر را دریافت می‌کنند.

پروژه متلب آماده  خلاصه‌ای از پیشرفت علمی در زمینه شبکه‌های عصبی به شرح زیر است:

• در سال ۱۹۴۳، مک‌کولوخ (McCulloch) و پیتس (Pitts) اولین مدل ریاضی نورون‌ها را پیشنهاد کردند و نشان دادند که چگونه می‌توان شبکه‌های نورن‌مانند را تحلیل و محاسبه کرد.
• نخستین ایده‌های یادگیری با شبکه‌های عصبی را هِب (Hebb) در کتابی با عنوان «سازمان‌دهی رفتار» در سال ۱۹۴۹ ارائه کرد.
• در سال ۱۹۵۱، ادموندز (Edmonds) و مینسکی (Minsky) ماشین یادگیری خود را با بهره‌گیری از ایده هب ساختند.
• نقطه مهم آغاز یادگیری شبکه نرون‌ را می‌توان کار روزنبلات (Rosenblatt) در سال ۱۹۶۲ دانست. روزنبلات دسته‌ای از شبکه‌های یادگیری نورون‌مانند ساده را ساخت که شبکه عصبی پرسپترون (Perceptron Neural Network) نامیده شد.
• جان هاپفیلد (John Hopfield) در مقاله مهمی که در سال ۱۹۸۲ منتشر کرد، یک معماری برای شبکه عصبی با نام شبکه هاپفیلد ارائه کرد. از این شبکه عصبی می‌توان برای حل مسائل بهینه‌سازی مانند مسئله فروشنده دوره‌گرد استفاده کرد.
• یک شبکه عصبی مهم که بسیار مورد استفاده قرار می‌گیرد، با یادگیری پس‌انتشار خطا (Backpropagation) یا BP است. شبکه عصبی پس‌انتشار خطا را اولین بار، وربوس (Werbos) در سال ۱۹۷۴ و پس از او روملهارت و همکارانش (Rumelhart et al) در سال ۱۹۸۶ ارائه کردند. کتاب‌ آن‌ها، با عنوان «پردازش توزیع شده موازی» (Parallel Distributed Processing)، چشم‌انداز گسترده‌ای از رویکردهای شبکه عصبی را بیان کردند.
• شبکه‌های عصبی با توابع پایه شعاعی (Radial Basis Functions) یا شبکه‌هاب عصبی RBF در سال ۱۹۸۸ معرفی شدند و به دلیل قابلیت تعمیم و ساختار ساده‌شان که از انجام محاسبات طولانی و غیرضروری جلوگیری می‌کرد، نسبت به شبکه‌های پیش‌خور (Feed-forward Network) یا MFNها توجه زیادی را به خود جلب کردند. تحقیقات مربوط به قضایای تقریب جامع (Universal Approximation) نشان دادند که هر تابع غیرخطی را می‌توان روی یک مجموعه فشرده (Compact Set) و با دقت دلخواه با شبکه عصبی RBF تقریب زد. همچنین تحقیقات گسترده‌ای درباره کنترل عصبی RBF سیستم‌های غیرخطی انجام شده که در حال حاضر نیز ادامه دارد.

در ادامه، مدل ریاضی یک شبکه ساده RBF و پیاده‌سازی آن در متلب را بیان می‌کنیم.

یک شبکه عصبی ساده RBF

شبکه‌های عصبی RBF سه لایه دارند: لایه ورودی (Input Layer)، لایه پنهان یا مخفی (Hidden Layer) و لایه خروجی (Output Layer). نورون‌های لایه مخفی با یک تابع پایه شعاعی (RBF) فعال (تحریک) می‌شوند. لایه مخفی از آرایه‌ای از واحدهای محاسباتی تشکیل شده که گره‌های مخفی (Hidden Nodes) نامیده می‌شوند. هر گره مخفی شامل یک بردار $$c$$ مرکزی است که یک بردار پارامتری با طولی مشابه با بردار ورودی $$x$$ است. فاصله اقلیدسی بین بردار مرکز و بردار ورودی $$x$$ شبکه به صورت $$||x\left(t\right)–c_j\left(t\right)||$$ تعریف می‌شود.

شکل ۲ مدل شبکه عصبی ساده‌ای را نشان می‌دهد. در این شکل، ورودی‌ها یا همان نورون‌های ورودی $$x_1$$ تا $$x_n$$ هستند. وزن‌ها نیز $$w_1$$ تا $$w_n$$ هستند که در هریک از ورودی‌ها ضرب می‌شوند. عنصر دیگر این شبکه عصبی تابع جمع $$Ne{t}_i$$ است که حاصل‌ضرب ورودی‌ها در وزن‌ها را جمع می‌کند. بخش دیگر این شبکه، تابع فعال‌سازی $$f$$ است. و در نهایت، خروجی بخش آخر این شبکه را تشکیل می‌دهد.

الگوریتم این شبکه عصبی را می‌توان به صورت زیر توصیف کرد:

$$Ne{t}_i=\sum _i{w}_{ij}{x}_j+b_i$$

$$u_i=f\left(Ne{t}_i\right)$$

$$y_i=g\left(u_i\right)=h\left(Ne{t}_i\right)$$

که در آن، $$g\left(u_i\right)=u_i$$ و $$y_i=f\left(Ne{t}_i\right)$$ است. مقدار $$b_i$$ نیز بایاس است.

تابع فعال‌ساز $$f\left(Ne{t}_i\right)$$ معمولاً به یکی از این سه صورت است:‌

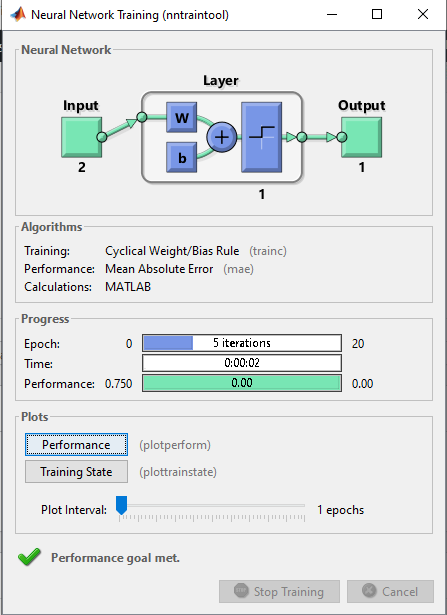
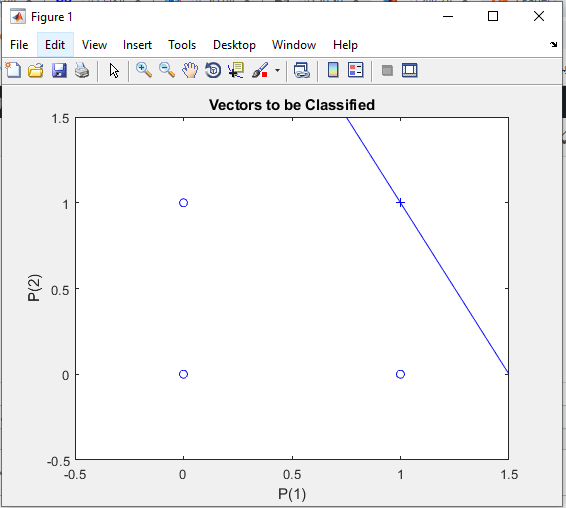
خروجی متلب: