حل معادله انتقال حرارت دوبعدی به روش ADI با متلب
حل معادله انتقال حرارت دوبعدی به روش ADI با نرم افزار متلب(مکانیک سیالات و ریاضی مهندسی) همراه داکیومنت لاتین و راهنمای فارسی: انجام پروژه متلب
در این برنامه میتوانید پارامترهای سیستم رو عوض کرد و برای هر سیستمی استفاده کرد و بهترین چواب را از آن گرفت .
در این سیستم از متد ADI در حل معادله گرما و حرارت استفاده شده است.
برای تابع در دستگاه مختصات دکارتی با متغیرهای مکانی و متغیر زمان ، معادله حرارت عبارت است از:
در حالت کلی تر:
که در اینجا ضریب مثبتی است که اصطلاحاً “پخشندگی گرمایی” یا “ضریب نفوذ گرمایی” نامیده می شود و میزان ضریب نفوذ هدایتی گرما را نشان میدهد. و عملگر نمایانگر لاپلاسین یک تابع است. در مسائل فیزیکی مربوط به تغییرات دما تابع در واقع نمایانگر دما در مکان و زمان میباشد، همچنین ضریب نفوذ حرارتی خواهد بود.
معادله حرارت یک معادله از نوع معادلات دیفرانسیل پاره ای سهموی میباشد که در شاخه های مختلف علمی کاربرد بسیار دارد. بعنوان مثال در نظریه احتمالات معادله حرارت با مطالعه حرکتهای براونی از طریق معادله فوکر-پلانک مرتبط میباشد. همینطور در بحث ریاضیات مالی، برای حل معادله دیفرانسیل پاره ایی بلک-اسکولز ابتدا از تبدیل این معادله به معادله حرارت استفاده میشود. و البتهمعادله نفوذ که حالت کلی تری از معادله حرارت است در مطالعه پدیده های نفوذ شیمیایی و عملیات انتقال جرم در مهندسی شیمی ظاهر میشود.
معادلات دیفرانسیل سهموی
مقالهٔ اصلی: معادلات دیفرانسیل سهموی
معادلات دیفرانسیل سهموی بهعنوان مدلهای ریاضی حاکم بر فرایندهای پخش و نشر یا بهزبانی عمومیتر، فرایندهای برگشتناپذیروابسته بهزمان کاربردهای فراوان و متنوعی پیدا میکنند. سادهترین نمونه از اینگونه معادلات، معادلهٔ حرارت است.
توضیح کلی
انجام پروژه متلب:راه حل یک معادله حرارت یک بعدی ، درجه حرارت (u) است. در ابتدای میله با یک مقدار بیشینه در یک سر x=0 و با نقطه پایانی عایق شده در سر دیگر x=1. همانطور که دیده می شود با نفوذ حرارت دما با گذر زمان به یک مقدار تعادلی میرسد.
فرض کنید تابعی همچون دما را در مکان توصیف می کند. این تابع در طول زمان با گسترش انرژی گرمایی در فضای مورد بررسی دچار تغییر می شود. معادله حرارت تغییر دما را در طول زمان مشخص می کند. تصویر سمت چپ تغییرات دما را در امتداد یک نوار فلزی نشان می دهد. معادله حرارت به خوبی بیانگر این اصل است که حرارت در طول زمان از نقطه ای به نقطه مجاورش نفوذ می کند و انرژی گرمایی هرگز خود به خود تولید نمی شود مگر در صورت وجود منبع حرارتی یا یه اصطلاح “چاهک گرمایی”.برای مثال وقوع واکنش شیمیایی در یک سامانه می تواند منبع تولید انرژی گرمایی در آن سامانه باشد.
معادله حرارت در در حساب آمار و احتمالات در توضیح رفتار ولگشت استفاده میشود که در حل مسائل بوجود آمده در ریاضیات مالی استفاده فراوان میشود.
جوابهای بنیادین
انجام پروژه متلب : جواب بنیادین، بهنتیجهٔ حل معادلهٔ حرارت، در ازای شرط اولیهٔ وجود یک منبع گرمایی نقطه ای در مکانی معلوم از جسم مورد بررسی اطلاق میشود. در حالت یکبعدی ) داریم:
که همان تابع دلتای دیراک (که برای مدل کردن یک بار حرارتی نقطه ای می باشد) است. حل این مسئله، همان جواب بنیادین را بهدست خواهد داد:
با در دست داشتن این جواب، همواره میتوان حل معادله یکبعدی حرارت را به ازاء هر شرط اولیهٔ معلوم با کانولوشن بهدست آورد:
خروجی برنامه :
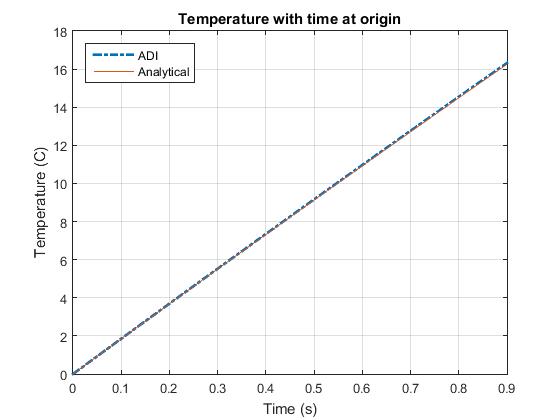
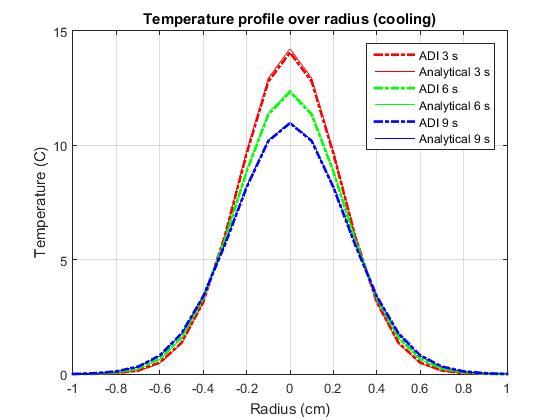
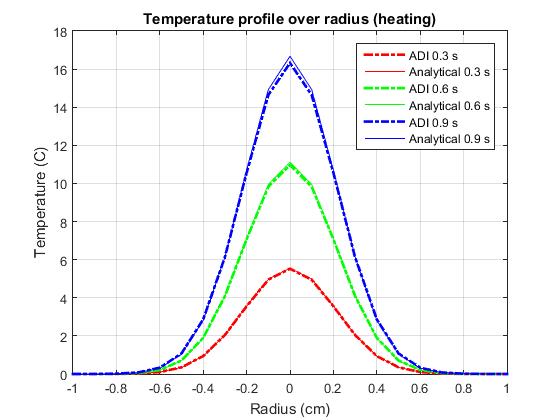
انجام پروژه متلب
صفحه اول سایت
حل معادله، انتقال حرارت ،دوبعدی، روش ADI ،نرم افزار متلب،مکانیک سیالات، ریاضی مهندسی،انجام پروژه متلب




لطفاً براي ارسال دیدگاه، ابتدا وارد حساب كاربري خود بشويد