مینیمم کردن خطای پرواز هواپیما با استفاده از فیلتر کالمن در متلب
مینیمم کردن خطای پرواز هواپیما با استفاده از فیلتر کالمن شبیه سازی در متلب :
فیلتر کالمن یک فیلتر بازگشتی کارامد است که حالت یک سیستم پویا را از یک سری اندازه گیریهای همراه با خطا بر آورد میکند. به همراه یک تنظیم کننده خطی مرتبه دوم (linear-quadratic regulator -LQR) فیلتر کالمن مسائل Gaussian control خطی مرتبه دوم (linear-quadratic-Gaussian control – LQG) را حل میکند. فیلتر کالمن ، LQR و LQG راه حلی هستند برای آنچه شاید اساسیترین مسائل تئوری کنترل می نامند.
مثالی برای کاربرد : تهیه اطلاعات پیوسته به روز و دقیق در مورد مکان و سرعت یک شی معین فقط به کمک توالی مشاهدات در مورد موقعیت آن شی، که هر کدام شامل مقداری خطاست امکان پذیر است. این فیلتر در طیف گستردهای از کاربریهای مهندسی از رادار گرفته تا بصیرت رایانهای کاربرد دارد. روش تصفیه کالمن یکی از عناوین مهم در تئوری کنترل و مهندسی سیستمهای کنترلی میباشد.
به عنوان مثال، برای کاربری آن در رادار، آنجا که علاقه مند به ردیابی هدف هستید، اطلاعات در مورد موقعیت، سرعت و شتاب هدف با حجم عظیمی از انحراف به لطف پارازیت در هر لحظه اندازه گیری میشود. فیلتر کالمن از پویایی هدف بهره میگیرد به این صورت که سیر تکاملی آن را کنترل میکند، تا تاثیرات پارازیت را از بین ببرد و یک برآورد خوب از موقیت هدف در زمان حال (تصفیه کردن) و در آینده (پیش بینی) و یا در گذشته (الحاق یا هموار سازی) ارائه میدهد. یک نسخه ساده شده فیلتر کالمن، فیلتر آلفا بتا (alpha beta filter)، که همچنان عموماً استفاده میشود از ثابتهای static weighting به جای ماتریسهای کواریانس استفاده میکند.
نام گذاری و تاریخچه توسعه : اگر چه Thorvald Nicolai Thiele و Peter Swerling قبلاً الگوریتم مشابهی ارائه داده بودند، این فیلتر به افخار Rudolf E. Kalman، فیلتر کالمن نام گذاری شد و Stanley F. Schmidt عموماً به خاطر توسعه اولین پیاده سازی فیلتر کالمن شهرت یافت. این رخدادهنگام ملاقات با کالمن در مرکز تحقیقاتی ناسا (NASA Ames Research Center) روی داد و وی شاهد کارائی ایده کالمن در برآورد مسیر پرتاب پروژه آپولو بود، که منجر به الحاق آن به رایانه ناوبری آپولو شد. این فیلتر بر روی کاغذ در ۱۹۵۸ توسط Swerling، در ۱۹۶۰ توسط Kalman و در ۱۹۶۱ توسط Kalman and Bucy ایجاد و بسط داده شد.
این فیلتر بعضی مواقع فیلتر Stratonovich-Kalman-Bucy نامیده میشود، چرا که یک نمونه خاص از فیلتر بسیار معمولی و غیر خطی ای است که قبلاً توسط Ruslan L. Stratonovich ایجاد شده، در حقیقت معادله این نمونه خاص، فیلتر خطی در اسنادی که از Stratonovich قبل از تابستان ۱۹۶۰، یعنی زمانی که کالمن ،Stratonovich را در کنفرانسی در موسکو ملاقات کرد به چاپ رسید بود.
در تئوری کنترل، فیلتر کالمن بیشتر به برآورد مرتبه دوم (LQE) اشاره دارد. امروزه تنوع گستردهای از فیلتر کالمن بوجود آمده، از فرمول اصلی کالمن در حال حاظر فیلترهای : کالمن ساده، توسعه یافته اشمیت، اطلاعاتی و فیلترهای گوناگون جذر بیرمن، تورنتون و بسیاری دیگر بوجود آمده اند. گویا مرسومترین نوع فیلتر کالمن فاز حلقهٔ بسته (phase-locked loop) میباشد که امروزه در رادیوها، رایانهها و تقریباً تمامی انواع ابزارهای تصویری و ارتباطی کاربرد دارد.
اساس مدل سیستم پویا فیلترهای کالمن بر اساس سیستمهای خطی پویا (linear dynamical systems) گسسته در بازه زمانی هستند. آنها بر اساس زنجیره ماکوف (Markov chain) مدل شده، به کمک عملگرهای خطی ساخته شده اند و توسط پارازیت گاشین (Gaussian noise) تحریک میشوند. حالت سیستم توسط برداری از اعداد حقیقی بیان میشود. در هر افزایش زمانی که در بازههای گسسته صورت میگیرد، یک عملگر خطی روی حالت فعلی اعمال میشود تا حالت بعدی را با کمی پارازیت ایجاد کند و اختیاراً در صورت شناخت روی کنترل کنندههای سیستم برخی اطلاعات مرتبط را استخراج میکند.
سپس عملگر خطی دیگر به همراه مقدار دیگری پارازیت خروجی قابل مشاهدهای از این حالت نامشخص تولید میکند. فیلتر کالمن قادر است مشابه مدل نامشخص مارکوف برخورد کند. با این تفاوت کلیدی که متغییرهای حالت نامشخص در یک فضای پیوسته مقدار میگیرند( نقطهٔ مقابل فضای حالت گسسته در مدل مارکوف). بعلاوه، مدل نامشخص مارکوف میتواند یک توزیع دلخواه برای مقادیر بعدی متغییرهای حالت ارائه کند، که در تناقض با مدل پارازیت گاشین ای است که در فیلتر کالمن استفاده میشود. در اینجا یک دوگانگی بزرگ بین معادلات فیلتر کالمن و آن مدل مارکوف وجود دارد. مقالهای در رابطه با این مدل و دیگر مدلها در Roweis and Ghahramani (1999) ارائه شده است.
درباره ی پرواز هواپیما، ﻓﺮﻣﻮل ﻫــﺎی ساده ای وجود دارد که حتی با استفاده از فیزیک اول دبیرستان هم می توانید آن را درک کنید و لی احتمالا درﺣـﺎل ﺣـﺎﺿﺮ ﻫﻤـﻪ آن ها را ﻓﺮاﻣﻮش ﮐﺮده اﯾﺪ اما اشکالی ندارد ما به زبانی ساده برای شما توضیح خواهیم داد. اولین چیزی که باید بدانید این است ﮐـﻪ اولین قانون تاثیرگذار این است که ﺗﻘـﺎﺑﻞ ﭼﻨﺪﯾـﻦ ﻧـﯿﺮوی ﻓﯿﺰﯾﮑﯽ با یکدیگر، ﻧﻘﺶ ﮐﻠﯿﺪی و اﺻﻠﯽ در ﮐﻞ ﻋﻤﻠﯿﺎت ﻋﺠﯿﺐ ﭘﺮواز را ایفا می کند.
ﻧﯿﺮوی ﭘﺴﺎر: به نیرویی می گویند که ﻣﻘﺎوﻣﺖ هوا را ﻗﺒﻞ از ﺷﺮوع بـﻪ ﺣﺮﮐـﺖ ﺗﻮﺳـﻂ ﻧـﯿﺮوی راﻧـﺶ که به آن تراست نیز می گویند، ﺧﻨﺜﯽ شود.
راﻧﺶ: در واقع ﻧﯿﺮوﯾﯽ اﺳﺖ ﮐﻪ ﻫﻮاﭘﯿﻤﺎ را ﺑﻪ ﺳﻤﺖ ﺟﻠﻮ ﻫﺪاﯾﺖ ﻣﯽ ﮐﻨﺪ . بر خلاف نیروی گرانش، این نیرو توسط موتورهای هواپیما تامین می شود.
ﻟﯿﻔﺖ: اﯾﻦ ﻧﯿﺮو در هواپیما وﻗﺘﯽ ﺗﻮﻟﯿﺪ ﻣﯽ ﺷﻮد ﮐﻪ ﻫﻮا ﺑﻪ ﻋﻠﺖ ﻓﺮم ﺧﺎص بال های ﻫﻮاﭘﯿﻤـﺎ، بدنه را ﺑﻪ ﺳﻤﺖ ﺑﺎﻻ ﻫﻞ ﻣﯽ دﻫﺪ.
ایرفول: برشی از سطح مقطع بال هواپیماها. ایرفول ها در واقع با عبور جریان هوا از دو طرف هواپیما ها سبب می شوند که فشار در سطح بالایی بال های هواپیما کاهش پیدا کند و فشار در سطح پایینی بال ها بیشتر از سطح بالایی آن ها شود و در نتیجه، هواپیما به سمت بالا حرکت می کند.
ﻧﯿﺮوی ﺟﺎذﺑﻪ: ﻧﯿﺮوﯾﯽ ﮐﻪ ﻫﺮ ﭼﯿﺰی ﺑﺮ روی اﯾﻦ ﮐﺮه ﺧﺎﮐﯽ را ﻣﺤﮑﻢ و ﺛﺎﺑﺖ ﺑـﻪ ﺧﻮد میب چسباند و همه چیز را به سمت خود جذب می نماید.
ﺣﺮﮐت های ﺣﻮل اهرم هواپیما که با ﭼﺮﺧﺶ ﯾﺎ رول ﻫﻮاﭘﯿﻤﺎ از ﻃﺮﯾﻖ ﺑﺎل های ﻫﻮاﭘﯿﻤﺎ اﻧﺠﺎم ﻣــﯽ ﺷـﻮد. در واقع آن ها ﺑﺎﻋﺚ ﻣﯽ ﺷﻮﻧﺪ ﮐــﻪ ﻫﻮاﭘﯿﻤﺎ ﺑﻪ دور ﺟﻬﺘــﯽ ﮐﻪ دﻣﺎﻏﻪ ی ﻫﻮاﭘﯿﻤــﺎ ﺑـﻪ سمت آن ﻣـﯽ رود، ﺑﭽﺮﺧﺪ. اﯾﻦ ﺣﺮﮐﺖ، ﭼﺮﺧﺶ ﻧﺎﻣﯿﺪه ﻣﯽ ﺷﻮد ﮐﻪ اﻟﺒﺘﻪ ﻧﺒﺎﯾﺪ آن را ﺑﺎ ﺣﺮﮐــﺖ دور زدن ﻫﻮاﭘﯿﻤﺎ ﺑﺮ روی زﻣﯿﻦ، اﺷﺘﺒﺎه ﮔﺮﻓﺖ.
ﺑﺮای ﺣﺮﮐﺖ ﻫﻮاﭘﯿﻤﺎ بر دور ﻣﺤﻮر ﭼﺮﺧﺶ، ﺧﻠﺒﺎن اﻫﺮم ﻫﺪاﯾﺖ ﻫﻮاﭘﯿﻤﺎ را در ﺟﻬﺖ ﭼﺮﺧﺶ چپ یا راست ﺣﺮﮐﺖ ﻣﯽ دﻫــﺪ و با آن کار در واقع ﻣﯽ ﺗﻮاﻧﺪ ﺑﻪ ﺳﻤﺖ ﭼﭗ ﯾﺎ راﺳﺖ برود. ﭼﺮﺧﺶ ﻣﺤﻮر ﻋﻤﻮدی ﻫﻮاﭘﯿﻤﺎ که با اﻧﺤﺮاف از ﻣﺴﯿﺮ نـﺎﻣﯿﺪه ﻣـﯽ ﺷـﻮد و ﺗﻮﺳـﻂ ﺳـﮑﺎن ﻣﺘﺤﺮک ﻋﻤﻮدی دم ﻫﻮاﭘﯿﻤﺎ ﮐﻨﺘﺮل ﻣﯽ ﺷﻮد. ﯾﮏ ﻫﻮاﭘﯿﻤﺎ ﺑﻼﻓﺎﺻﻠـﻪ ﻧﺴـﺒﺖ ﺑـﻪ ﺣﺮﮐـﺖ ﺳـﮑﺎن ﻋﻤﻮدی ﻣﺘﺤﺮک ﻋﮑﺲ اﻟﻌﻤﻞ ﻧﺸﺎن می دهد. در ﻫﻮاﭘﯿﻤﺎﻫﺎی ﺟﺪﯾﺪ، ﺑـﺎ ﭼﺮخ های ﻗﺎﺑﻞ ﮔﺮدش ﻫﻮاﭘﯿﻤﺎ ﻣﺮﺗﺒﻂ ﻣﯽ ﺑﺎﺷﺪ.
ﺣﺮﮐﺖ ﺣﻮل ﻣﺤﻮرﻋﺮﺿﯽﻫﻮاﭘﯿﻤﺎ اﯾﻦ اﺟﺎزه را می دهد ﺗﺎ ﺑﻪ ﺳﻤﺖ ﭘﺎﯾﯿﻦ و ﯾﺎ ﺑـﻪ ﺳﻤﺖ ﺑﺎﻻ ﭘﺮواز ﻧﻤﺎﯾﺪ. ﻫﻨﮕﺎﻣﯽ ﮐﻪ اﻫﺮم ﻫﺪاﯾﺖ ﻫﻮاﭘﯿﻤﺎ را ﺑـﻪ ﺳﻤﺖ ﻋﻘﺐ ﺑﮑﺸﯿﺪ، ﻫﻮاﭘﯿﻤــﺎ ﺑﻪ ﺳﻤﺖ ﺑﺎﻻﺣﺮﮐﺖ ﺧﻮاﻫﺪ ﮐﺮد و ﻫﻨﮕﺎﻣﯽ ﮐـﻪ آن را ﺑﻪ ﺳﻤﺖ ﺟﻠﻮ ﻓﺸﺎر دﻫﯿﺪ، ﻫﻮاﭘﯿﻤﺎ ﺣﺮﮐﺘﯽ ﺑﻪ ﺳﻤﺖ ﭘﺎﯾﯿﻦ ﺧﻮاﻫﺪ داﺷﺖ. ﻧﯿﺮوﻫﺎی وارده ﺑﻪ ﻣﺤﺾ اﯾﻦ ﮐﻪ ﺷﻤﺎ ﺷﺮوع ﺑﻪ ﻣﺎﻧﻮر دادن و ﺗﻐﯿﯿﺮ ﻣﺴﯿﺮﺳﺮﯾﻊ می کنید، در ﺳﺮﻋﺖ ﻫﺎی ﺑـﺎﻻ فشار وارد می شود و اهرم فشارها آﺷﮑﺎر ﻣﯽ ﺷﻮﻧﺪ.
مینیمم کردن، خطای، پرواز هواپیما، فیلتر کالمن، شبیه سازی،متلب،متلب،پروزه متلب،matlab ،matlab project، kalman filter
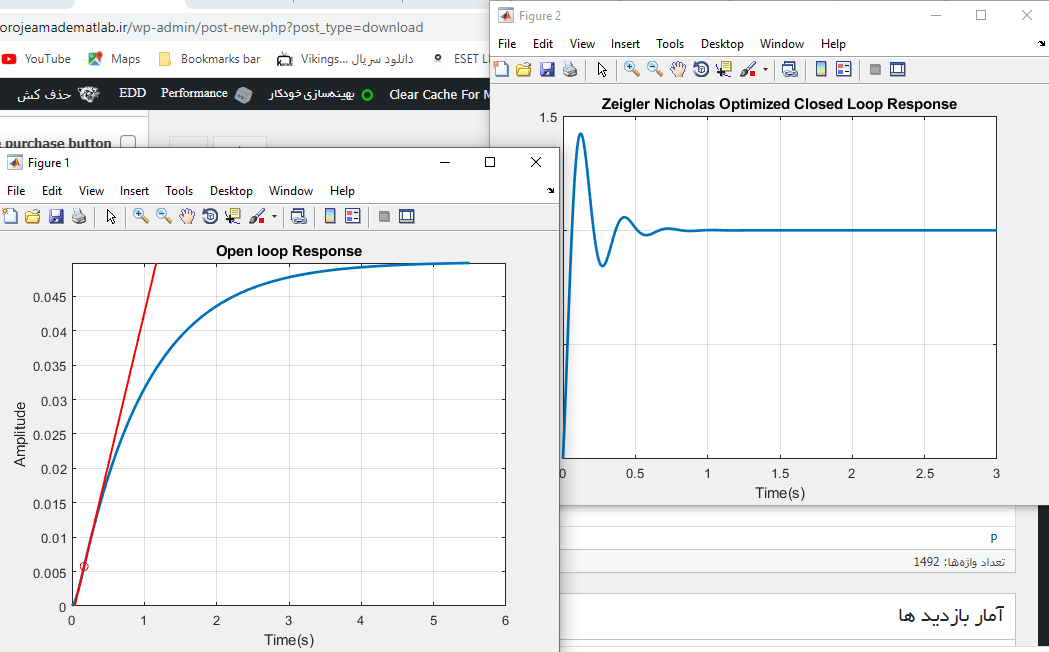
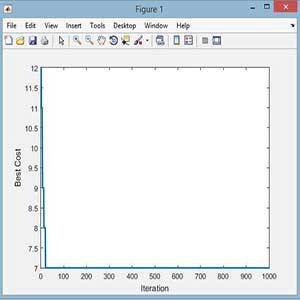
خروجی متلب :

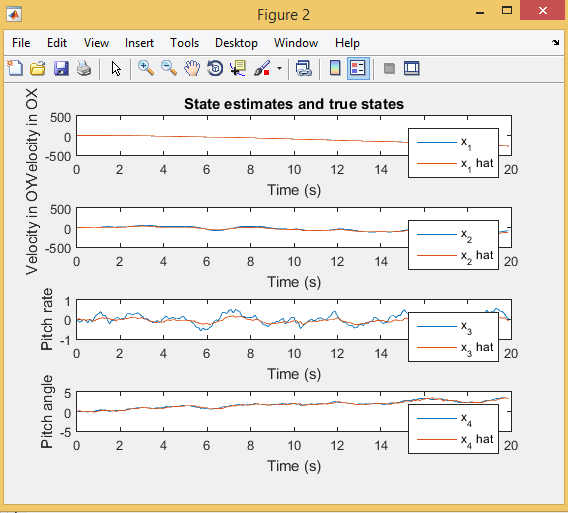
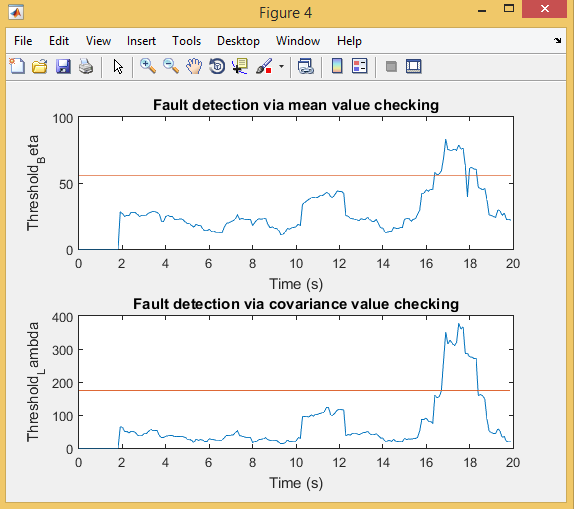
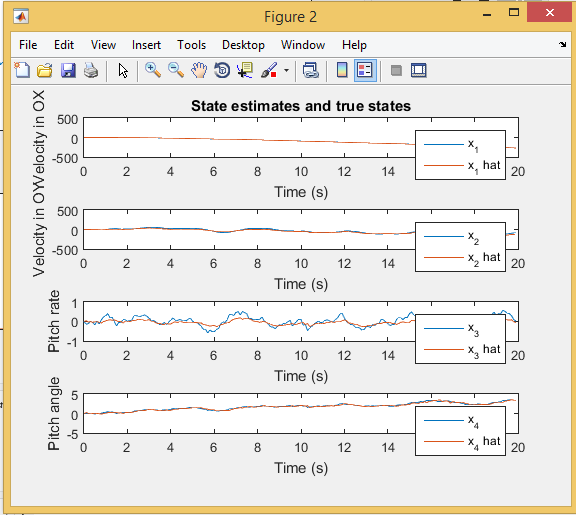
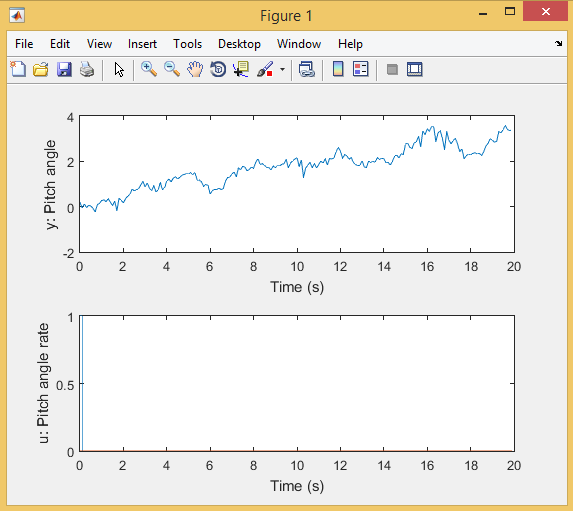

لطفاً براي ارسال دیدگاه، ابتدا وارد حساب كاربري خود بشويد