سیستم جرم و فنر با شبکه عصبی در متلب :پروژه متلب
سیستم جرم و فنر با شبکه عصبی در متلب پروژه کامل شبکه عصبی :پروژه متلب
ارتعاش آزاد
پروژه متلب : «ارتعاش آزاد» (Free Vibration) به پدیدهای گفته میشود که در آن، یک سیستم بدون تاثیرپذیری از نیروی خارجی متغیر، نوسان کند. در این نوع از ارتعاش، نیروی ذخیره شده در سیستم، جابجایی اولیهای را در آن ایجاد میکند. مثلا جرم و فنری را در نظر بگیرید که در محیطی بدون اصطکاک قرار گرفته است. با جابجا کردن سیستم به میزانی اندک و سپس رها کردن آن، جرم شروع به نوسان خواهد کرد.
اگر دقت داشته باشید، در سیستم جرم و فنر فقط نیروی گرانش است که حرکت جرم را رقم میزند؛ به همین دلیل، نوسان مذکور به عنوان ارتعاش آزاد در نظر گرفته میشود. در یک سیستم الاستیک، ارتعاش آزاد به سه دسته تقسیمبندی میشود:
- ارتعاش طولی: زمانی که ذرات سیستم، موازی با محور جسم نوسان کنند.
- ارتعاش عرضی: به ارتعاشی گفته میشود که ذرات جسم، عمود بر محور آن نوسان کنند.
- ارتعاش پیچشی: نوعی از ارتعاش است که در آن ذرات جسم، حول محورش (روی یک دایره) نوسان کنند.
ارتعاش اجباری
پروژه متلب به ارتعاشی اتلاق میشود که در آن سیستم، تحت یک نیروی متغیر خارجی، نوسان میکند. مثالی که در ادامه آمده، توضیح بیشتری از این مفهوم را ارائه میدهد. زمانی که یک پاندول تحت نیروی گرانش نوسان میکند هیچ نیروی خارجی متغیری به آن وارد نمیشود. اما اگر در هر نوسان سیستم، ضربهای به آن بزنیم، ارتعاش مد نظر از نوع اجباری خواهد بود.
اجزاء تشکیلدهنده یک سیستم ارتعاشی
یک سیستم ارتعاشی شامل بخشهای مختلفی میشود. این اجزا، با چهار مولفه اصلی نیرو، جابجایی، سرعت و شتاب در ارتباط هستند. با بهکارگیریِ سیستم جرم و فنر، ارتباط بین نیرو و جابجایی مدلسازی میشود. البته توجه داشته باشید که در حالت کلی میتوان با استفاده از قانون دوم نیوتن یا معادله اویلر لاگرانژ، معادلات توصیف کننده سیستمهای دینامیکی را بدست آورد. در یک فنر خطی، نیروی FS با ازدیاد طول آن و به صورت خطی تغییر میکند. بنابراین با فرض اینکه ازدیاد طول فنری برابر δ=x2-x1 باشد، نیروی ناشی از این تغییر طول، معادل با مقدار زیر خواهد بود.
![]()
در این معادله، k برابر با سختی فنر و x1 و x2 طول اولیه و نهایی فنر هستند.
میراگر (دمپر) ویسکوز
میراگر، جزئی از سیستم است که میان نیرو و سرعت ارتباط برقرار میکند. این اِلمان از استوانهای تشکیل شده که در آن مایعی قرار گرفته است؛ پیستون درون این مایع جابجا شده و باعث میشود هنگام نوسان، نیرویی را در خلاف جهت حرکت، به سیستم وارد کند. رابطه میان نیروی میراگر و سرعت پیستون نسبت به استوانه، به صورت زیر است.
در این معادله، c به عنوان «ضریب میرایی ویسکوز» (Viscous Damping Coefficient) در نظر گرفته میشود. مقدار ‘x’۲-x1، اختلاف سرعت در حالت اولیه و نهایی پیستون را نشان میدهد. همچنین رابطه بین شتاب پیستون و نیروی وارد شده به آن را میتوان با استفاده از قانون دوم نیوتن، به صورت زیر محاسبه کرد.
![]()
در این معادله، m برابر با جرم فنر در نظر گرفته شده است. در شکل زیر میتوانید اجزاء تشکیل دهنده دو سیستم ارتعاشی را ملاحظه کنید.
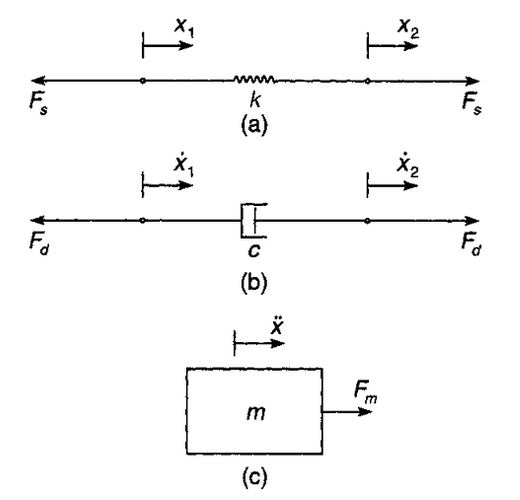
دقت کنید که در شکل بالا جرمِ فنر و دمپر ناچیز در نظر گرفته شده است.
سختی معادل فنر
پروژه متلب فنرها همچون مقاومتهای الکتریکی، در یک سیستم ارتعاشی میتوانند به صورت موازی و یا متوالی مورد استفاده قرار گیرند. همچنین هر سیستم ارتعاشیِ الاستیک را میتوان به صورت یک فنر در نظر گرفت. با این فرض، میتوان عددی تحت عنوان ثابت معادل فنر (Keq) را به سیستم ارتعاشی مذکور اختصاص داد. در جدول زیر چند سیستم ارتعاشی به همراه ثابت معادل آنها ارائه شده است.
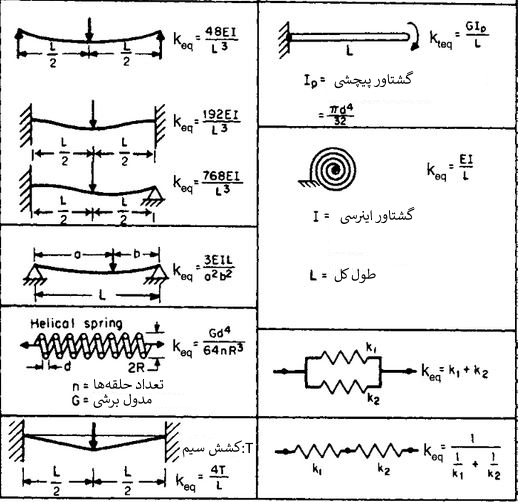
تمامی سیستمهای نشان داده شده در بالا را میتوان با یک جرم و فنر معادلسازی کرد. در حالت پیچشی نیز این معادلسازی امکانپذیر است. در چنین سیستمی، گشتاور، معادل با نیرو و زاویه پیچش، معادل با جابجایی خطی در نظر گرفته میشوند.
معادله حرکت
پروژه متلب اکثر سیستمهای مکانیکی را میتوان با تقریب بسیار خوبی با سیستم جرم-فنر-دمپر، مدلسازی کرد. مطابق با شکل زیر نیروهای وارد شده به جرم، در چنین سیستمی را میتوان با استفاده از قانون دوم نیوتن، به شکل زیر نشان داد.
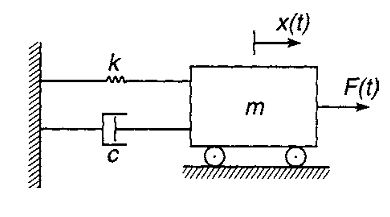
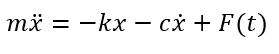
این معادله را میتوان به صورت زیر نوشت.
![]()
پروژه متلب رابطه مذکور، یک معادله دیفرانسیل مرتبه دوم است. همانطور که در مطالب گذشته نیز اشاره کردیم، چنین معادلاتی را میتوان با استفاده از روش ترکیب خطی پاسخ خصوصی و عمومی محاسبه کرد. شرایط اولیه این معادله را میتوان به صورت x0 و ۰‘x در نظر گرفت. این مقادیر به ترتیب جابجایی و سرعت در زمان صفر هستند. به منظور حل این معادله در ابتدا فرض کنید که با سیستمی سروکار داریم که نیروی خارجی و دمپر در آن وجود ندارد. بنابراین در معادله ذکر شده در بالا عبارات (F(t و c، صفر هستند. در نتیجه این معادله به صورت زیر خواهد بود.
![]()
پروژه متلب با مرتب کردن، این معادله به شکل زیر خواهد شد.
![]()
در این معادله wn2=k/m در نظر گرفته شده است. به منظور حل آن، پاسخ (x(t را به صورت زیر در نظر میگیریم.
![]()
بنابراین معادله مشخصه مرتبط، به شکل زیر است.
![]()
احتمالاً از ریاضیات به خاطر دارید، که ریشههای این معادله به صورت مختلط و برابر با s=±iwn خواهند بود. ریشه مختلط یعنی اینکه پاسخ معادله به صورت نوسانی است. با توجه به ریشههای یافت شده، پاسخ معادله دیفرانسیل به شکل زیر در نظر گرفته میشود.
![]()
ثوابت A و Φ را میتوان با استفاده از شرایط اولیه سرعت و جابجایی محاسبه کرد.
توجه داشته باشید که از نظر دستهبندی، این ارتعاش از نوع آزاد است، چراکه در آن عامل اولیه باعث نوسان شده و نیروی خارجی متغیری به سیستم وارد نمیشود. در این سیستم wn، Φ و A بهترتیب اختلاف فاز، فرکانس طبیعی و دامنه نوسان نامیده میشوند. زمان لازم برای یک نوسان کامل را «دوره» (Period) مینامند که برابر با T=2π/wn است؛ همچنین معکوس دوره تحت عنوان «فرکانس طبیعی» (Natural Frequency) شناخته میشود و آن را با Fn نشان میدهند.
نوسان آزاد سیستمهای میرا
در این قسمت قصد داریم تا در مورد نوسان سیستمهای میرا بحث کنیم. نیروی خارجی وارد شده در معادله اصلی برابر با صفر در نظر گرفته میشود. در نتیجه این معادله را برای یک سیستم میرا میتوان به صورت زیر نوشت. در حالت کلی هرچه اجزای تشکیل دهنده یک سیستم ارتعاشی افزایش یابند، معادلات حاکم بر سیستم نیز پیچیدهتر میشود؛ از این رو پیشنهاد میشود ترجیحا با استفاده از معادله اویلر لاگرانژ معادلات حرکت یک سیستم را بیابید.
![]()
در این معادله، ξ ضریب میرایی و نشاندهنده میزان میرایی سیستم با گذشت زمان است. مهمترین حالت میرایی، زمانی است که این ضریب بین صفر و یک قرار داشته باشد. این حالت از ارتعاش میرا را «زیر میرایی» (Under Damped) مینامند. با توجه به فرضیات انجام شده، معادله کلی به صورت زیر در میآید.
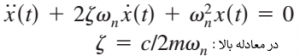
در این معادله، wd را «دوره میرایی» (Period of Damped Oscillation) مینامند که برابر با wd=2π/T است.
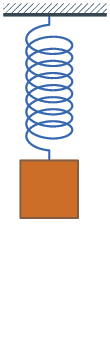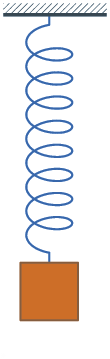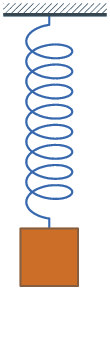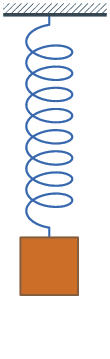
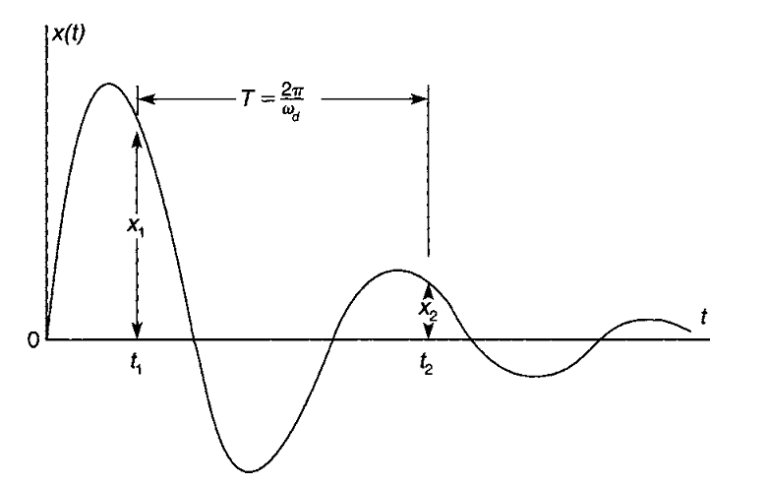
همانطور که در انیمیشن و شکل بالا نیز مشاهده میشود، در حالت زیر میرایی، سیستم پس از چند نوسان به حالت تعادل خود میرسد. حالت ξ=۱، شرایط ویژهای در میرایی است که تحت عنوان «میرایی بحرانی» (Critical Damping) شناخته میشود. این حالت هنگامی است که سیستم پس از چندین نوسان به حالت تعادل خود میرسد. در طراحی سیستمهای تعلیق، تلاش بر این است تا این نوع از میرایی در سیستم ایجاد شود.
به حالت دیگری از میرایی که در آن ضریب ξ بیشتر از ۱ در نظر گرفته میشود، «فرامیرایی» (Overdamped) گفته میشود. در این حالت ریشههای معادله مشخصه به صورت حقیقی هستند. بنابراین فرآیند میرایی به صورت نمایی و با سرعت بیشتری اتفاق میافتد.
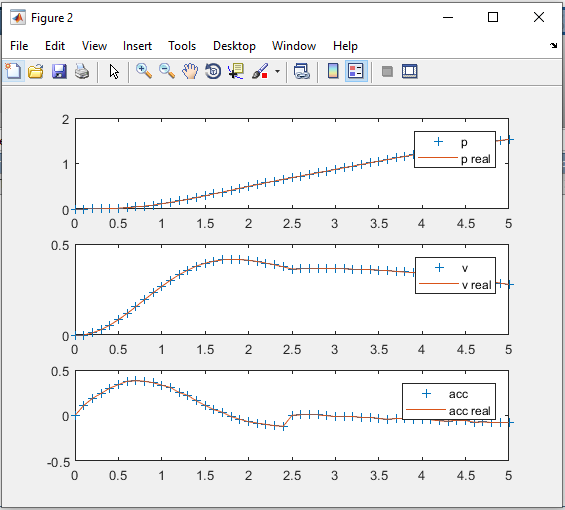
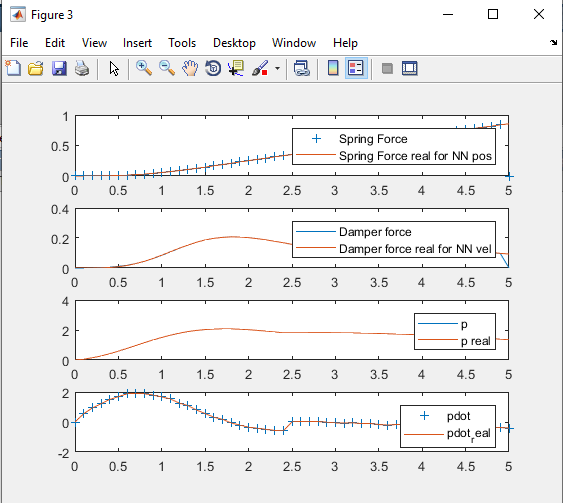
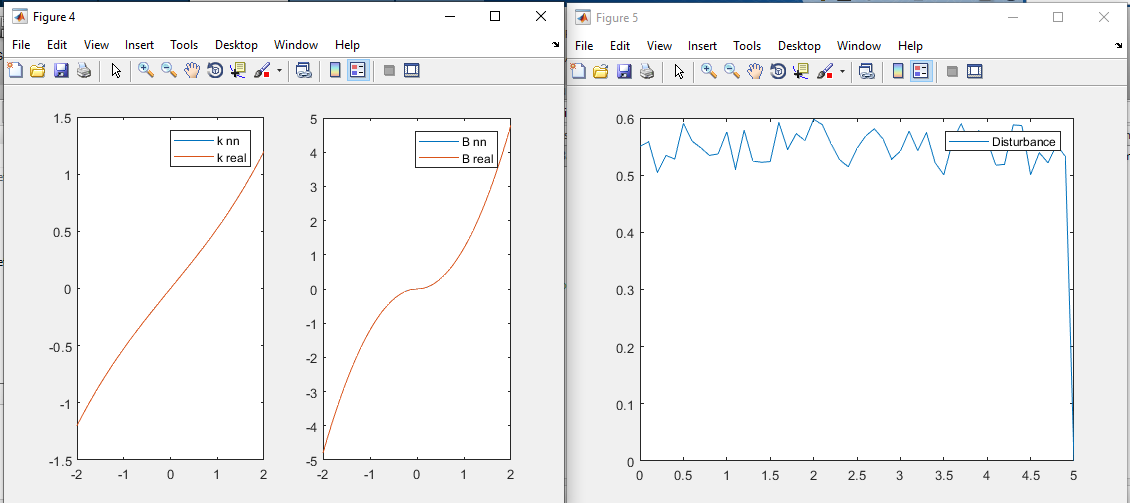
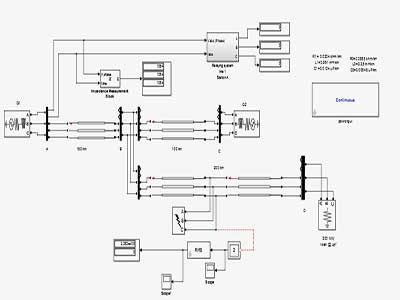
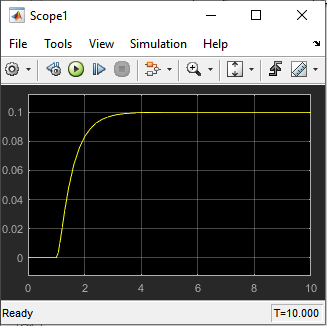
خروجی متلب :
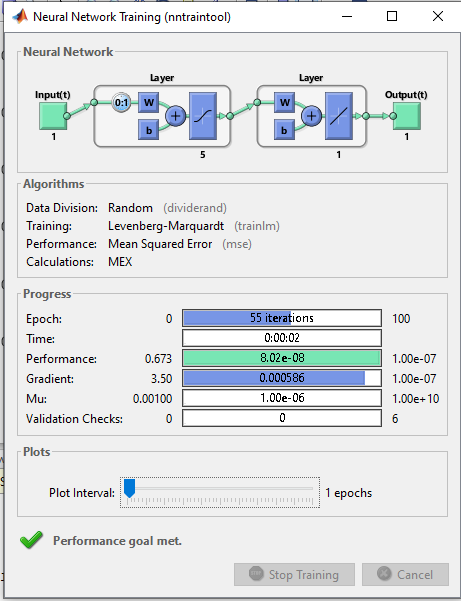
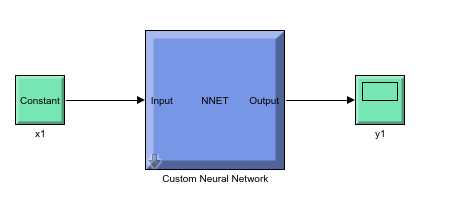

لطفاً براي ارسال دیدگاه، ابتدا وارد حساب كاربري خود بشويد