کنترل دور موتور مغناطیس دائم PMSM با استفاده از کنترلر fuzzy بهمراه گزارش فارسی
کنترل دور موتور مغناطیس دائم PMSM با استفاده از کنترلر fuzzy بهمراه گزارش فارسی :پروژه متلب
پروژه متلب :کنترلر شامل دو ورودی می باشد و یک خروجی که با دبل کلیک برروی هر کدام مجموعه های فازی را مشاهده می کنیم و با دبل کلیک بر روی موتور استنتاج قوانین فازی را مشاهده می نماییم.
موتورهای DC به دلیل کارایی بالا و ساختار مناسب بطور وسیع به عنوان سرو موتور مورد استفاده قرار می گیرند. این موتورها دارای راندمان بالا و سرعت پاسخ سریع هستند ، اما کیفیت آنها بدلیل خوردگی در نتیجه اصطکاک ایجاد شده در اثر تماس مکانیکی بین جاروبکها و کموتاتور و جرقه های ناشی از آن محدود می باشد . این امر باعث شده تا به نگهداری و بازرسی مداوم ، از قبیل تمیز کردن یا عوض کردن جاروبکها نیازمند باشند. علاوه بر این موتورهای DC با مسائلی همانند ، عدم توانایی تحمل اضافه بار و غیر مقاوم بودن ، گشتاور پایین و محدوده کم تغییرات سرعت روبرو هستند. به همین دلیل موتور های AC با وجود اینکه دارای کنترل کننده های پیچیده و گرانقیمت تر نسبت به موتور های DC هستند، مورد توجه روز افزون قرار گرفته اند. موتورهای مغناطیس دائم در سالهای اخیر و بخصوص در دهه اخیر به دلیل خصوصیات ذاتی نظیر چگالی, توان بالا , لختی کم , ضریب توان و بازده بالا نسبت به موتورهای DC و موتورهای القایی در بسیاری از کاربردهای صنعتی سرعت متغییر در گستره توان کم و متوسط به خصوص در کاربردهای با رفتار برتر ترجیح داده شده اند. در این فصل سعی شده تا قبل از ارائه و بکارگیری روش کنترل به بررسی عملکرد این نوع موتورها ، انواع متداول و بطور کلی معرفی موتورهای سنکرون مغناطیس دائم پرداخته شود.
پروژه متلب :در این پایاننامه که مشتمل چهار فصل است، کنترل دور موتور dc به طور جامع توضیح داده شده است.
از آنجایی که برای شبیهسازی مدلها از SimUlink و برای بخشهای کنترلی از SimUlink Response Optimization استفاده شده است، در بخش مقدمه، توضیحی اجمالی بر این موضوعات داشتهایم.
در فصل اول، در باره درایوهای dc با استفاده از بلوکهای SimUlink ,simpower و بلوک NCD (با تغییر گشتاوربار و سرعت ) توضیح داده شده است.
در فصل چهارم، کلیه بخشهای استفاده شده در فصل سوم مدلسازی شدهاند و کنترل دور موتور dc با استفاده از بلوک NCD توضیح داده شده است.
در پایان لازم است که از زحمات استاد گرامی ،جناب آقای دکتر سروی که در ارائه این پروژه مرا راهنمایی کردند،تشکر کنم.
مقدمهای بر SimUlink
از آنجائی که در بخشهای مختلف، برای مدلسازی وشبیهسازی، ما از SimUlink استفاده کردهایم سعی میکنیم در این فصل به طور خلاصه درباره ایجاد مدل در Sim U link برخی بلوکهای آن که در فصلهای مختلف از آن استفاده شده است، توضیح میدهیم.
چهار بلوک اصلی که در نمایش تمام سیستمهای پیوسته خطی به کار میروند عباتنداز : بلوک بهره، بلوک جمع ، بلوک مشتق ، بلوک انتگرالگیر.
علاوه بر این چهار بلوک اصلی ، بلوک تابع تبدیل نیز اغلب در مدل سازی سیستمهای فیزیکی و کنترل کننده استفاده میشود . بنابراین هر کدام از این بلوکها را به اختصار توضیح میدهیم.
- بلوک بهره : خروجی این بلوک ، حاصلضرب ورودی آن در یک مقدار ثابت است . توجه میکنیم که خروجی به طور پیوسته از ورودی تبعیت میکند. یعنی
این بلوک در commonly used block از simulink library یافت میشود .
- بلوک جمع : این بلوک حداقل یک ورودی و دقیقاً یک خروجی دارد . اگر تعداد ورودیها زیاد باشد ، بهتر است از چند بلوک جمع متوالی استفاده شود . ( به منظور بهتر خواندن )
این بلوک در commonly used block از simulink library یافت میشود.
- بلوک مشتق : این بلوک یک ورودی و یک خروجی دارد. این بلوک در continuos از simulink library یافت میشود .
- بلوک انتگرالگیر : این بلوک نیز، یک ورودی و یک خروجی دارد. این بلوک در continuos از SimUlink library یافت میشود .
- بلوکهای تابع تبدیل :
SimUlink دو بلوک برای پیاده سازی تابع تبدیل دارد .
- transfer Fcn : این بلوک در continuos از Sim U link library یافت میشود و دارای دو فیلد است : الف- Numerator شامل ضرایب صورت با توانهای کاهشی s
ب- Denominator شامل ضرایب مخرج با توانهای کاهشی s
- Zero – Pole : این بلوک در continuos از SimUlink library یافت میشود و دارای سه فیلد است .
الف – zero صفرهای تابع تبدیل
ب – pole قطبهای تابع تبدیل
ج – gain اندازه تابع تبدیل
- بلوک MATLAB Fcn : از این بلوک در فصل ۳ ، استفاده شده است ، این بلوک مانند بلوک Fcn یک بلوک غیر خطی است . بلوک MATLAB Fcn سرعت کمتری نسبت به بلوک Fcn دارد ولی نسبت به Fcn اولیت دارد چون این بلوک قادر به محاسبات ماتریسی است در صورتی که بلوک Fcn این قابلیت را ندارد . این بلوک در user – definded function از SimUlink library یافت میشود .
- بلوک ثابت constant : این بلوک که در source library یافت میشود برای ایجاد مقداری ثابت که میتواند برداری یا اسکالر باشد به کار میرود .
- بلوک محدود کننده (saturation ) این بلوک برای پیاده سازی بلوک غیر خطی اشباع به کار میرود. این بلوک دارای یک حد بالا(Upper limit) و یک حد پایین Lower limit میباشد. هرگاه مقدار ورودی بین حدود باشد، مقدار خروجی برابر مقدار ورودی خواهد بود، اگر ورودی از Upper limit بیشتر شود، خروجی برابر حد بالا و اگر ورودی از Lower limit کمتر شود، خروجی برابر حد پایین میشود. این بلوک در Discontinuties از simUlink library یافت میشود.
- Manual switch : هرگاه میخواهیم ورودی بین دو مقدار Switch کند از این بلوک استفاده میکنیم. با دوبار کلیک کردن روی این بلوک، ورودی بین دو مقدار تعین شده، Switch میکند. این بلوک در Commonly Used block یافت میشود.
- بلوک زمین (Ground) : این بلوک به منظور جلوگیری از ایجاد پیغام خطا توسط سیمولینک به ورودیها استفاده شده متصل میگردد. این بلوک در Commonly Used block یافت میشود.
- بلوک To workspace و بلوکC lock :
این دو بلوک در sim U link بسیار کاربرد دارند. بلوک To workspace، سیگنال ورودی خود را در ماتریس MATLAB ذخیره میکند. این سیگنال بعد از توقف شبیهسازی در فضای کاری MATLAB قابل دستیابی است. این بلوک در Sink از sim U link library یافت میشود.
بلوک Clock نیز، سیگنالی متشکل از زمان فعلی شبیهسازی تولید میکند. این بلوک در Source یافت میشود.
در واقع برای اینکه بعد از پایان شبیهسازی، سیگنالی را در Work space مشاهده کنیم از این دو بلوک استفاده میکنیم. سیگنالی را که میخواهیم مشاهده کنیم به یک بلوک To workspace وصل میکنیم و بلوک Clock را به یک بلوک To workspace دیگر وصل میکنیم. نکته بسیار مهم که باید به آن توجه کرد این است که در هر دو بلوک To workspace، باید Structure را به Array تغییر دهیم. اکنون با استفاده از دستور Plot که در Work space MATLAB تایپ میکنیم، میتوانیم بعد از پایان شبیهسازی نمودار سیگنال مربوطه را بر حسب زمان مشاهده کنیم.
- بلوک OUT : برای ایجاد دریچه خروجی برای زیر سیستم به کار میرود. این بلوک در Commonly Used block یافت میشود.
- بلوک IN : برای ایجاد ورودی برای زیر سیستم به کار میرود. این بلوک در Commonly Used block یافت میشود.
- بلوک Scope : از آنجائیکه بلوک Scope در Simulation مکرراً به کار میرود این بلوک را به طور کامل توضیح میدهیم.
بلوک Scope تقلیدی از اسیلوسکوپ میباشد. این بلوک بخشی از سیگنال ورودی که میتواند برداری یا اسکالر باشد را نمایش میدهد. گستره عمودی (محور y) و گستره افقی (زمان روی محور x) را میتوان با هر مقدار مورد نظر تنظیم نمود. محور افقی مقدار واقعی سیگنال ورودی را نمایش میدهد. درجهبندی محور افقی همواره از صفر شروع میشود و به مقدار مشخص شده با عنوان Time range خاتمه مییابد. بنابراین، مثلاً اگر گستره افقی ۱۰ و زمان فعلی ۱۰۰ باشد، داده ورودی برای دوره ۹۰ تا ۱۰۰ نمایش داده میشود؛ اگر چه عنوان محور افقی هنوز صفر تا ۱۰ میباشد. اهداف اولیه بلوک Scope برای استفاده حین شبیهسازی میباشد، اما بلوک قابلیت ایجاد کپی پرینت شدهای از تصویر را نیز داراست. به علاوه بلوک Scope میتواند سیگنالی که ترسیم میکند را برای تحلیل اضافی و ترمیم، مثلاً با استفاده از دستور Plot یا دستور Simplot ، به کاری MATLAB ارسال نماید.
بلوک Scope را میتوانید بدون اتصال خط سیگنال به ورودی به آن و با پیکربندی آن به صورت بلوک Scope شناور در مدل قرار دهید. بلوک Scope شناور از هر خط سیگنالی که در حین اجرای شبیهسازی کلیک میکنید، به عنوان ورودی استفاده خواهد کرد.
دکمههای بلوک Scope عبارتند از:
- دکمه Zoom : دکمه Zoom امکان تمرکز روی ناحیهای از نمایشگر را فراهم میکند.
- دکمه Zoom x : امکان تمرکز روی بخشی از نمایشگر را بدون تغییر مقیاس عمودی، فراهم میکند.
- دکمه Zoom y : دکمه Zoom y امکان تمرکز روی بخشی از نمایشگر را بدون تغییر مقیاس افقی، فراهم میکند.
- Auto scale : مقیاس عمودی را به نحوی تغییر میدهد که حد پایین آن برابر حداقل مقدار سیگنالی که هماکنون نمایش داده میشود و حد بالایی آن برابر حداکثر مقدار سیگنالی که اکنون نمایش داده میشود، باشد. برای مقیاسبندی مجدد نمایشگر، حین شبیهسازی نیز میتوانید Auto scale را کلیک کنید.
- Save axies : مقیاس فعلی را مقیاس پیشفرض بلوک Scope قرار میدهد. اگر مقیاس را تغییر داده و سپس شبیهسازی را بدون اینکه ابتدا Save axis را کلیک کنید، مجدداً اجرا نمایید؛ با شروع شبیهسازی مقیاس به مقدار پیشفرض بر خواهد گشت.
- دکمه Open Properties window کادر مکالمه ویژگیهای بلوک Scope را باز میکند. این کادر مکالمه امکان تنظیم مقیاس پیش فرض بلوک Scope و ارسال داده به فضای کاری MATLAB را فراهم میکند.
کادر مکالمه ویژگیهای Scope دارای دو صفحه است:
- صفحه General که دارای فیلدهایی برای تنظیم تعداد محورها و گستره زمانی و کنترل فاصلهگذاری بین نقاط ترسیم میباشد.
- صفحه Data history دارای فیلدهایی برای کنترل اندازه بافر داده Scope و ارسال داده نمایش یافته به فضای کاری MATLAB میباشد.
صفحه General از دو بخش تشکیل شده است. بخش محورها که تعداد و پیکربندی محورها را کنترل میکند. فیلد Number of axes تعداد محورهای نشان داده شده در پنجره Scope و تعداد ورودیهای بلوک Scope را کنترل میکند. برای هر محور، یک ورودی را خواهیم داشت، انتخاب Floating Scope بلوک Scope را به بلوک Scope شناور تبدیل میکند، که ورودی را ندارد و دادههای خط سیگنالی را که حین اجرای شبیهسازی انتخاب شده است، نمایش میدهد. Time range مقیاس محور زمان را کنترل میکند. اگر Time range روی Auto تنظیم گردد، گستره مقیاس از صفر تا زمان نهایی شبیهسازی خواهد بود. اگر Time range روی عدد بزرگتر از صفر تنظیم گردد، گستره مقیاس از صفر تا مقدار تعیین شده خواهد بود. Tick lable منویی کرکرهای است که میتواند all، برای قرار دادن درجه بندی زمانی روی هر محور زمانی، none، برای نداشتن درجهبندی زمانی یا Bottone axies only برای درجهبندی فقط روی محور x انتخاب شود.
بخش نمونهبرداری صفحه General شامل فهرستی کرکرهای است که در برگیرنده دو گزینه Decimation و Sample time میباشد. اگر Decimation انتخاب شود، در فیلد داده متناظر، ضریب تقسیم که باید عددی صحیح باشد، قرار داده میشود. اگر Decimation انتخاب گردد و برابر را تنظیم شود تمام نقاط ورودی بلوک رسم میشوند. اگر Decimation برابر ۲ تنظیم گردد، نقاط یک درمیان رسم میشوند و الی آخر. اگر Sample time انتخاب شود، در فیلد داده بایستی فاصلهگذاری مطلق بین نقاط ترسیم وارد شود. بلوک Scope نقاط ورودی را در یک بافر ذخیره میکند. اندازه این بافر را میتوان با استفاده از Data history تنظیم نمود. Limit Points to Last را انتخاب کنید و مقداری را برای تعیین اندازه بافر وارد نمایید مثلاً اگر Limit rows to Last برابر ۱۰۰۰ تنظیم شود و شبیهسازی کلاً ۲۰۰۰ نقطه تولید نماید، پس از پایان شبیهسازی تنها ۱۰۰۰ نقطه پایانی در دسترس میباشد.
تنظیم محور y :
برای تنظیم محور y ، نمایشگر Scope را کلیک راست کنید. در کادر مکالمه ظاهر شده، Axies Properties را انتخاب کنید. کادر مکالمه دیگری ظاهر میشود، این کادر مکالمه دارای فیلدهایی برای ورود حدود محورها و مشخص کردن عنوان محور میباشد.
xy Graph
بلوک xy Graph نموداری همانند نمودار ایجاد شده توسط دستور Plot در MATLAB ایجاد میکند. Xy Graph دو ورودی اسکالر میپذیرد. محور افقی و عمودی را بایستی با استفاده از کادر مکالمه بلوک پیکربندی نمایید.
برای ایجاد یک مدل در simUlink مراحل زیر را طی میکنیم:
سیمولینک یکی از متعلقات MATLAB است و بایستی از درون MATLAB با کلیک آیکون سیمولینک در نوار ابزار MATLAB، یا با وارد کردن فرمان simUlink در اعلان MATLAB فراخوانی شود. با این کار مرورگر کتابخانه سیمولینک باز خواهد شد. کلیک آیکون New window، یک پنجره مدل خالی باز میکند. در این پنجره مدل خالی که Untitled نامگذاری شده استف مدل سیمولینک را ایجاد خواهیم کرد. آیکون کتابخانه سیمولینک را دوبار کلیک میکنیم تا کتابخانه سیمولینک باز شود. توجه میکنیم که قاب سمت راست شامل لیستی از کتابخانهها میباشد.
- بعد از بازکردن پنجره مدل، از کتابخانه simUlink (کتابخانههای داخل simUlink مثل Source ، Sinks ؟، Math ، …) بلوکهای خود را انتخاب میکنیم.
بعضی از بلوکها (در کار ما) لازم است از کتابخانه های دیگر به مدل کپی شوند. مثل بلوک منبع ولتاژ، بلوک اندازهگیری ولتاژ، پالس ژنراتور یکسوساز که از کتابخانه Simpower و یا بلوک NCD که از کتابخانه simUlink Response Optimization به مدل کپی میشوند.
- بلوکهای انتخابی را به داخل پنجره مدل میکشیم.
- بین بلوکها سیگنال قرار میدهیم.
- اگر از وسط یک سیگنال (خط) بخواهیم یک خط دیگر خارج کنیم Control را گرفته و با موس خط را میکشیم.
- برای برگرداندن بلوک، بلوک را انتخاب میکنیم وسپس Format: Flip Block را انتخاب میکنیم.
- برای برگرداندن بلوک، بلوک را انتخاب کرده سپس Format: Flip Block را انتخاب میکنیم.
- برای سایهزدن بلوک، بلوک را انتخاب کرده، سپس Format: Show Drop Shadow را انتخاب میکنیم.
- برای تغییر اندازه بلوک، بلوک را انتخاب کرده، سپس یکی از دستگیرهها را میکشیم.
- برای ویرایش نام بلوک، نام بلوک را کلیک میکنیم.
- برای پنهان کردن نام بلوک، نام بلوک را انتخاب کرده سپس Format: Hide Name را انتخاب میکنیم.
- برای برگرداندن نام بلوک، نام بلوک را انتخاب کرده سپس Format: Hide Name را انتخاب میکنیم
- برای حذف شیء، شیء را انتخاب کرده و سپس Edit: Clear را انتخاب میکنیم.
- برای عنواندهی خط سیگنال کنار خط دوبار کلیک میکنیم و سپس متن را تایپ میکنیم.
- برای اضافه کردن عبارات توضیحی به مدل جایی را که میخواهیم عبارات توضیحی را وارد نماییم، دوبار کلیک میکنیم، سپس متن را تایپ میکنیم.
- برای اجرا Simulation ، روی Scope دوبار کلیک میکنیم Simulation-Start را انتخاب میکنیم.
- برای Save کردن مدل، از File>Save as استفاده میکنیم.
برای تنظیم زمان شبیهسازی از Simulation> Configuration استفاده میکنیم. در پایان به ایجاد زیر سیستم در simUlink اشاره میکنیم:
دو روش برای ایجاد زیرسیستم وجود دارد:
- استفاده از پوشینهدار کردن بخشی از مدل موجود:
قسمتی از مدل را که میخواهیم زیر سیستم باشد با کادر محصور میکنیم و از گزینه Edit: Create Subsystem استفاده میکنیم. بلوک زیر سیستم ایجاد میشود. برای باز کردن زیر سیستم روی آن دوبار کلیک میکنیم.
- استفاده از بلوک زیر سیستم از کتابخانه بلوک سیگنالها و سیستمها:
پنجره مدل را باز میکنیم، از کتابخانه بلوکی سیگنالها و سیستمها، بلوک زیرسیستم را انتخاب کرده و به پنجره مدل میکشیم. روی بلوک زیرسیستم کلیک میکنیم، پنجره دیگری باز میشود و در این پنجره زیر سیستم را مدل میکنیم سپس پنجره را میبندیم. (بدون save کردن)
بلوکهای نقابدار :
نقابزنی مفهوم خلاصهسازی را توسعه میبخشد. اگر یک زیر سیستم تبدیل به زیر سیستم نقابدار شود، لازم نیست برای تنظیم gainها و مقدار اولیه انتگرال زیر سیستم، آن را باز کرده و تکتک مواد را تنظیم کنیم بلکه با دو بار کلیک کردن روی بلوک نقابدار، کادر مکالمه آن باز میشود و تمام پارامترها را همان جا تنظیم میکنیم.
مراحل ایجاد بلوک نقابدار:
- یک زیرسیستم (از طریق روش درم که در بالا توضیح داده شد) ایجاد میکنیم.
- بلوک زیر سیستم را انتخاب کرده و Edit: mask subsystem را انتخاب میکنیم.
مقدمهای بر Simulink Response Optimization :
Simulink Response Optimization یک (Graphical User Interface) GUI را فراهم میکند که در طراحی سیستمهای کنترل و سیستمهای فیزیکی ما را یاری میکند.
برای استفاده از Simulink Response Optimization ما فقط نیاز داریم که یک بلوک خاص، به نام بلوک Signal Constraint را در دیاگرام simUlink قرار دهیم.
هر بلوک را به سیگنالی از مدل که قرار است روی آن قیود و مرزهایی (نظیر Over shoot، Setting time، Rise time، …) قرار دهیم وصل میکنیم. Simulink Response Optimization این قیود را به قیود یک مسئله بهینهسازی تبدیل میکند و سپس مسئله را حل میکند. البته این حل بوسیله روتینهای بهینهسازی که از Optimization Toollbox و Genetic Algorithm and Direct Search Toolbox گرفته میشود، صورت میگیرد.
مسئله قیود بهینهسازی که به وسیله Simulink Response Optimization، به طور تکراری فرمولبندی شده است ، برای شبیهسازی سیستم simUlink فراخوانده میشود، سپس نتایج با قیود هدف مقایسه میشود و از روشهای شیب برای تنظیم پارامترها استفاده میشود.
لازم به ذکر است که ما میتوانیم هر تعداد متغیر simUlink، شامل اسکالرها، بردارها، ماتریسها را با وارد کردن نام متغیر در dialog box مناسب، تنظیم کنیم. علاوه بر این ما میتوانیم قیود نامعلوم را روی متغیرهای مدل به منظور رسیدن به بهترین طراحی جابهجا کنیم.
در این فصل سعی میشود، ابتدا توضیحی کلی درباره کار با Simulink Response Optimization داده شود، و سپس جزئیات کار، به تفصیل در صفحات بعد توضیح داده میشود.
به طور کلی برای استفاده از Simulink Response Optimization باید مراحل زیر را طی کنیم:
- ابتدا یک مدل (غیر خطی) از سیستم و کنترل کننده با استفاده از MATLAB میسازیم. سیگنالهای ورودی (به طور مثال Steps ، ramps ، Observed data) را اضافه میکنیم.
- یک بلوک Signal Constraint به سیگنالهایی که میخواهیم محدود شود (روی آنها میخواهیم قیود قرار دهیم) وصل میکنیم. این بلوک در Simulink Response Optimization. از simUlink librar y browser یافت میشود.
- اگر در حال حاضر پارامترهای مدل در space MATLAB Work موجود نمیباشند، این پارامترها را در Work space وارد میکنیم.
- با دوبار کلیک کردن روی هر بلوک Signal Constraint در سیستم، پنجره Signal Constraint برای خروجی مورد نظر باز میشود.
- روش مورد نظر خود (برای محدود کردن سیگنال پاسخ) را از بین Enforce single bounds و یا Track refrence signal در انتهای پنجره Signal Constraint انتخاب میکنیم. در مورد این دو روش به تفضیل در بخشهای بعد توضیح خواهیم داد.
- در پنجره Signal Constraint ما میتوانیم قیود و یا مرزهای مورد نظر (نظیر Over shoot ، Setting time و یا Rise time …) را با کلیک کردن روی آن مرز وکشیدن آن و یا با راست کلیک کردن روی عبارت مرزی و انتخاب Edit از Menu اصلاح کنیم.
سیگنال مرجع را با انتخاب Goals>Desired Response در پنجره Signal Constraint و وارد کردن بردارهای داده برای سیگنال مرجع، تعریف میکنیم.
با انتخاب Optimization> Uncertain Parameters از پنجره Signal Constraint ما میتوانیم پارامترهای نامعلوم (پارامترهایی که مقدار دقیق آنها در مدل تعیین نشده و فقط حدود آن را میدانیم) را به پروژه بهینهسازی خود اضافه کنیم. برای این کار باید روی گزینه Add کلیک کنیم تا پارامترهای مورد نظر به لیست اضافه شوند.
- پروژه را Save میکنیم برای این کار از File> Save استفاده میکنیم. در ضمن با استفاده از File>load میتوانیم پروژه ذخیره شده را load کنیم. برای save کردن و reload کردن اتوماتیک مدل simUlink ، در انتهای Check box, Save dialog box را انتخاب میکنیم.
- از منوی Start, Optimization را انتخاب میکنیم تا سیگنال پاسخ با تنظیم پارامترهایی که (به عنوان پارامترهای تنظیم شده) واردکردهایم، بهینه گردد.
Optimization Progress window مقادیر جدید این پارامترها را نشان میدهد.
حالا که با مراحل کلی بهینهسازی (Optimization) یک سیگنال آشنا شدیم، میتوانیم هر یک از این مراحل را به تفضیل توضیح دهیم.
همانطور که گفتیم بعد از این که پارامترهای مدل را در Work space MATLAB وارد کردیم به سراغ پنجره Signal Constraint میرویم و با دو بار کلیک کردن روی آن، این پنجره را باز میکنیم. همانطور که درشکل زیر میبینیم این پنجره از منوهای مختلفی تشکیل شده است که سعی در توضیح این منوها داریم.
برای اولین قدم، به توضیح روشهای بهینهسازی میپردازیم.
هنگامی که پاسخ بله را برای سیستم خود بهینه میکنیم، یک روش مناسب برای قرار دادن قیود روی پاسخ بله، این است که مشخصات پاسخ بله مطلوب از قبیل rise time ، Setting time و Over shoot را تعریف کنیم. آنگاه Simulink Response Optimization پارامترهایی را که ما به عنوان پارامترهای تنظیم شده و نامعلوم وارد کردهایم را طوری تعیین میکند، که پاسخ بله حاصل دارای همین مقادیر برای rise time، setting time، over shoot باشد. برای تعریف مشخصات پاسخ بله، در پنجره Signal Constraint Goals>Desired Response را انتخاب میکنیم و یا در Figure window (پنجره شکل) کلیک را ست کرده و سپس Desired Response را انتخاب میکنیم. با این کار پنجره Desired Response نمایش داده میشود در بالای این پنجره دو گزینه وجود دارد که ما گزینه Specify step response characteries را انتخاب میکنیم تا مشخصات پاسخ بله به صورت زیر نمایش داده شود.
سه بخش بالا جزئیات بله خروجی را تعریف میکنند. این جزئیات عبارتند از:
Initial Value : سطح ورودی قبل از وقوع بله
Step time : زمانی که بله اتفاق میافتد.
Final value : سطح ورودی بعد از وقوع بله
گزینههای باقیمانده مشخصات سیگنال پاسخ را تعریف میکنند.
هر کدام از مشخصات پاسخ بله در زیر توضیح داده شده است:
Rise time : زمان لازم برای سیگنال پاسخ تا به یک درصد معین از مقدار نهایی پله برسد.
Rise% : درصد مقدار نهایی پله که در Rise time بدست میآید.
Setting time : زمان لازم قبل از اینکه سیگنال پاسخ در مرز درصد معینی از مقدار نهایی پله باقی بماند.
Setting % :درصد مقدار بله نهایی که در Setting time استفاده میشود.
over shoot% : درصد مقدار نهایی پله که به سیگنال پاسخ اجازه داده میشود، از مقدار نهایی پله تجاوز نکند.
Under shoot% : درصد مقدار اولیه بله که به سیگنال پاسخ اجازه داده میشود، از مقدار اولیه پله کمتر باشد.
مقادیر تعریفی برای پاسخ را در پنجره Response Specification وارد میکنیم. (بر اساس مدل) و سپس روی Ok کلیک میکنیم. این قیود روی شکل منعکس میشوند.
علاوه بر این روش، (یعنی تعریف مشخصات پاسخ بله خروجی)، ما میتوانیم پاسخ خروجی مطلوب را به عنوان یک ideal و Reference trajectory تعریف کنیم. برای این کار، ابتدا در انتهای پنجره Signal Constraint گزینه Track reference signal را انتخاب میکنیم. سپس درمیان Figure axes، سیگنال مرجع (reference signal) را رسم میکنیم. (البته با استفاده از تکنیکهای زیر). ما میتوانیم Track reference signal را به جای و یا همراه با enforcing signal bounds استفاده کنیم.
بعد از انتخاب Track reference signal گزینه Goal>Desired Responseانتخاب میکنیم و یا در پنجره Figure window راست کلیک میکنیم و Desired response را انتخاب میکنیم. با این کار پنجره Desired response باز خواهد شد. در این پنجره گزینه با عنوان Specifying reference signal برای نمایش reference signal setup به صورت زیر ظاهر میشود.
سیگنال مرجع را با وراد کردن بردارها و یا متغیرها از Work space برای زمان و دامنه سیگنال تعریف میکنیم، سپس Ok را کلیک میکنیم. برای On یا Off کردن سیگنال مرجع روی Figure window کلیک راست میکنیم و سپس Show>references signal را انتخاب میکنیم.
لازم است متذکر شویم که ما میتوانیم چندین سیگنال مختلف را در پنجره Signal Constraint رسم کنیم. این سیگنالها شامل سیگنالهای مرجع، سیگنالهای پاسخ اولیه و سیگنالهای پاسخ که در طول بهینهسازی بوجود میآیند، هستند.
- سیگنالهای مرجع (References signal) :
برای رسم یک سیگنال مرجع از روشهای موجود در Specifying reference signal (همان طور که توضیح دادیم) استتفاده میکنیم.
- سیگنالهای جاری (Current Response) :
برای نمایش سیگنالهای Current Response بر پایه مقادیر پارامترهای جاری در محورهای پنجره Signal Constraint کلیک راست میکنیم. و سپس Current Response Plot را انتخاب میکنیم. لازم به ذکر است که Current Response به صورت خطوط ضخیم سفید ظاهر میشوند.
- سیگنالهای اولیه (initial response) :
برای On یا Off کردن نمایش سیگنال initial response در محورهای پنجره Signal Constraint کلیک راست میکنیم و سپس Show>initial response را انتخاب میکنیم. initial response پاسخ سیگنال بر اساس مقادیر پارامترها قبل از اینکه بهینهسازی را run کنیم، میباشد. این سیگنال به صورت خطوط آبی ظاهر میشود.
- Intermediate steps
برای On یا Off کردن نمایش سیگنال پاسخ در Intermediate steps در طول بهینهسازی در محورهای پنجره Signal Constraint کلیک راست میکنیم و سپس Show>intermediate steps را انتخاب میکنیم. سیگنال پاسخ در یک Intermediate steps بر اساس مقادیر پارامتر در یک نقطه متوسط در بهینهسازی رسم میشود:
به طور کلی ما میتوانیم ویژگیهای نمودارهای پاسخ را تغییر دهیم. برای انجام این کار باید از Property Editor dialog box استفاده کنیم. Property Editor شامل دو گزینه زیر میباشد:
- Lables :
برای تعریف عنوان جدید برای عنوان (title) و نامهای (labels) محورها، رشته جدید را در Field که میخواهیم تغییر دهیم، تایپ میکنیم. توجه دهید که labe ها به سرعت هنگامی که ما تایپ میکنیم، تغییر میکنند.
- Limits :
مقادیر پیش فرض برای axes limit مقادیر ماکزیمم و مینیمم x و y نمایش داده شدهاند. اگر ما میخواهیم تنظیمات پیش فرض را تغییر دهیم، باید مقادیر در limits field را تغییر دهیم. Auto-scale box فوراً ظاهر میشود، اگر ما روی یک Different field کلیک کنیم. Limitهای جدید فوراً در نمودار پاسخ ظاهر میشوند. برای دوباره برقرار کردن مقادیر پیش فرض دوباره Auto-scale box را انتخاب میکنیم.
قبل از اینکه بهینهسازی (Optimization) را run کنیم، ما باید پارامترهای سیستم که میخواهیم تنظیم گردند، را تعریف کنیم. این کار باعث میشود که Simulink Response Optimization با تنظیم این پارامترها، سیگنال پاسخ خروجی، به قیود مورد نظر خود (نظیر overshoot، setting time، rise time … خود) برسد.
علاوه بر این ما میتوانیم پارامترهای دیگری را به صورت نامعلوم (Uncertain) تعریف کنیم.
- تعریف پارامترهای تنظیمپذیر در مدل:
Simulink Response Optimization، سیگنالهای پاسخ مدل را به وسیله تغییر پارامترهایی که ما به عنوان پارامترهای تنظیمپذیر درمدل تعریف کردهایم، بهینه میکند تا اینکه سیگنالهای پاسخ درون مرزهای قیود قرار بگیرد، یا به سیگنال پاسخ تعریف شده نزدیک شود. ما میتوانیم این پارامترهای تنظیمپذیر (که قرار است تنظیم شوند) را با انتخاب Optimization>Tuned Parameters در یک پنجره Signal Constraint تعریف کنیم.
- اضافه کردن پارامترهای تنظیمپذیر (Adding Tuned Parameters)
در پنجره Tuned Parameters یک لیست در سمت چپ نشان داده میشود. برای اضافه کردن پارامتری که قصد تنظیم آن را داریم روی دکمه Add کلیک میکنیم. با این کار Select Parameters dialog box شامل یک لیست از متغیرهای مدل که در Structure MATLAB موجود هستند ظاهر میشوند (اگر یک پارامتر هماکنون در لیست پارامترهای تنظیمپذیر لیست شده است آن پارامتر در Select Parameters dialog box ظاهر نخواهد شد.)
پارامترهایی که میخواهیم تنظیم شوند، انتخاب میکنیم و سپس Ok را کلیک میکنیم، تا آنها را به لیست پارامترهای تنظیمپذیر اضافه کنیم. برای حذف یک پارامتر از لیست پارامترهای تنظیمپذیر، آن پارامتر را انتخاب میکنیم و Delete را کلیک میکنیم.
- تغییر مشخصات پارامترهای تنظیمپذیر:
برای نمایش تنظیمات برای یک پارامتر تنظیمپذیر، آن پارامتر را از لیست Tuned Parameters انتخاب میکنیم، تنظیمات آن در سمت راست زیر Optimization settings ظاهر خواهد شد.
این تنظیمات شامل:
- Name : نام متغیر
- Value : مقدار جاری پارامتر (مقداری که پارامتر در حال حاضر دارد)
- Initial guess : مقدار اولیه استفاده شده برای الگوریتم بهینهسازی
لازم به ذکر است که یک حدس اولیه خوب میتواند سرعت بهینهسازی را بالا ببرد.
- Minimum : مقدار مینیمم یا Lower bound که ما میخواهیم پارامتر اختیار کند را، در این Field قرار میدهیم. به صورت پیش فرض این Field به صورتInf –تنظیم شده است. ما میتوانیم این field مقدار مینیمم دیگر را اصلاح کنیم.
- Maximum : مقدار ماکزیمم یا Upper bound که ما میخواهیم پارامتر اختیار کند را در این field قرار میدهیم. به صورت پیش فرض این field به صورت Inf+ تنطیم شده است. ما میتوانیم این field را با یک مقدار ماکزیمم دیگر را اصلاح کنیم.
- Scaling factory : پارامترهایی تنظیمپذیر بوسیله تقسیم مقدار جاریشان بوسیله یک Scaling Factory Scale میشوند (نه Normalized)
مقدار پیش فرض Scaling factory، مقدار اولیه پارامتر است. ما میتوانیم این مقدار را با یک Scaling factory دیگر اصلاح کنیم.
- Tuned : این Check-box نشان میدهد که این پارامتر، یک پارامتر تنظیمپذیر است. اگر ما نمیخواهیم این پارامتر در طول بهینهسازی تنظیم گردد، این گزینه را Un-check میکنیم. اما میتوانیم آن را در لیست پارامترهای تنظیمپذیر (برای بهینهسازی بعدی) نگه داریم.
بعد از اینکه ما پارامترهای تنظیمپذیر را تنظیم کردیم، Ok را کلیک میکنیم تا تغییرات انجام شده، Save گردد و از پنجره Tuned window خارج میشویم.
- تعریف پارامترهای نامعلوم (Uncertain) در مدل:
در یک Plant ممکن است پارامترهایی وجود داشته باشند که مقدار دقیق آن معلوم نباشد، ولی مقدار اسمی و میزان تغییرات آن معلوم باشد.
Simulink Response Optimization به ما اجازه میدهد تا با دو روش مختلف زیر در طراحیمان این پارامترهای نامعلوم را وارد کنیم. این دو روش عبارتند از:
- Passive mode : این روش سیگنالها را فقط بر اساس مقادیر نامی پارامترهای نامعلوم بهینه میکند.
- Active mode : در این روش سیگنالها بر اساس دو مقدار نامی پارامتر و همچنین مقادیر نامعلوم پارامتر، بهینه میشوند. لازم به ذکر است که این روش بیشتر از “Passive mode” استفاده میشود.
برای تعریف پارامتری به صورت پارامتر نامعلوم Optimization>Uncertain Parameters را از پنجره Signal Constraint انتخاب میکنیم.
توجه میکنیم که هنگامی که ما بیشتر از یک بلوک Signal Constraint در مدلمان داریم، پارامترهای نامعلوم را فقط در یک پنجره تعریف میکنیم.
به صورت پیش فرض Account for parameter uncertainly check box چک شده است. این موضوع نشان میدهد که ما میخواهیم پارامترهای نامعلوم را در پروژه بهینهسازی خود قرار میدهیم. با Unckeching این گزینه ما میتوانیم پارامترهای نامعلوم را بدون حذف اطلاعات، خاموش (غیر فعال) کنیم.
ما اکنون در لیست Uncertain Parameters وارد شدهایم.
- اضافهکردن پارامترهای نامعلوم :
برای اضافه کردن یک پارامتر نامعلوم جدید به لیست Uncertain Parameters باید Add button را کلیک کنیم. با این کار Select patameters dialog box که شامل یک لیست از پارامترهای مدل که در Work space MATLAB موجود هستند، را نمایش میدهد.
پارامترهایی که ما میخواهیم به صورت نامعلوم اضافه کنیم، را انتخاب میکنیم و سپس Ok میکنیم، تا این پارامترها به لیست پارامترهای نامعلوم اضافه شوند. برای حذف پارامترها از لیست پارامترهای نامعلوم، پارامتر را انتخاب میکنیم و سپس Delete را میزنیم.
- تغییر مشخصات پارامترهای نامعلوم :
برای بدست آوردن پارامترهای نامعلوم، دو روش نمونه برداری وجود دارد. هر دو روش از چندین مقدار پارامترهای نمونه برداری به صورت نامعلوم، استفاده میکنیم.
- روش اول Random (Monte carlo) : این روش، بهینه سازی را میان چندین مقدار پارامترهای تصادفی Random) (به صورت نامعلوم ، انجام میدهد. هنگامی که این روش انتخاب میشود، ما همچنین باید یک مقدار برای number of samples ( که تعداد پارامترهای تصادفی (Random) که simulink Response optimization استفاده میکند، رانشان میدهد،) وارد کنیم. یرای هر پارامتر در لیست پارامترهای نامعلوم، ما میتوانیم مقدار نامی پارامتر و همچنین رنج تغییر پارامتر که مقادیر ماکزیمم و مینیمم که پارامتر می تواند اختیار کند رانشان میدهد را تغییر دهیم.
هنگامی که بیشتر از یک پارامتر نامعلوم وجود دارد. ترکیبات پارامترهای تصادفی از میان مستطیل تعریف شده بوسیله مقادیر ماکزیمم ومینیمم همه پارامترها، انتخاب میشود. برای مثال در مورد دو پارامتر نامعلوم b و aبا رنج مقادیر به ترتیب ۰ تا ۳ و از ۱ تا ۲٫۵ مقادیر نمونهبرداری – که به وسیله نقاط سیاه نشان داده شدهاند – به طور تصادفی در مستطیل نشان داده شده در شکل زیر پراکنده شدهاند.
- روش دوم Grid : این روش بهینهسازی را در چندین مقدار تعریف شده برای پارامترهای نامعلوم قرار میدهد. برای هر پارامتر، ما میتوانیم در لیست پارامترهای نامعلوم، مقدار نامی و مچنین یک بردار از مقادیر پارامترهای نمونهبرداری، تعریف کنیم. برای مثال در مورد دو پارامتر نا معلوم a وb با مقادیر نمونهبرداری به ترتیب [۳ ۲ ۱ ۰] و [۲٫۵ ۲ ۵ ۱] مقادیر نمونهیرداری – که با نقاط سیاه ناشن داده شدهاند، در شکل زیر نشان داده شده است.
بر ای افزایش سرعت محاسبه، ما نمیتوانیم از همه مقادیر پارامترهای تصادفی در پروژه بهینهسازی، استفاده کنیم برای اینکه از مقادیر نامی پارمترهای نامعلوم در پروژه بهینهسازی، استفاده کنیم باید در Check box مربوطه گزینه Nominal response را انتخاب کنیم و سپس All sample parameter value با Min & Max value only را انتخاب کنیم. این گزینهها ترکیبات مقادیر همه پارامترهای نمونهبرداری و یا ترکیب مقادیر ماکمزیمم و مینیمم پارامتر را به ترتیب، شامل میشود. به این ترتیب فقط پاسخهای بهینه شده برای تنظیم پارامترهای تنظیم پذیر (که قصد تنظیم آنها را داریم)، به کار گرفته میشوند. پاسخهایی که بر مبنای سایر مقادیر پارامترهای نمونهبرداری، بدست میآیند نیز ممکن است در پنجره Signal constraint رسم شود.
بعد از اینکه پارامترهای تنظیمپذیر و پارامترهای نامعلوم را تعریف کردیم و روش بهینه سازی را از میان دو روش Tracking references sgnals و یا enforcing signal bounds انتخاب کردیم، نوبت به Run کردن بهینهسازی میرسد.
- Run کردن بهینهسازی:
هنگامی که ما قیود را تعریف کردیم و پارامترهای تنظیمپذیر و نامعلوم را تنظیم کردیم، میتوانیم بهینهسازی را run کنیم. اگر بهینهسازی برای اولین بار همگرا نشود، اغلب بعد از تنظیم قیود و یا تنظیم مشخصات پارامترهای تنظیم پذیر و یا انتخاب گزینههای مختلف، همگرا میشود. در بخش بعدی، پیشنهاداتی برای چگونگی تنظیم گزینههای بهینهسازی و گزینهها Simulation با استفاده از بهینهسازی ارائه میدهیم.
Simulink Response Optimization از الگوریتمهای بهینهسازی برای پیدا کردن مقادیر پارامترها استفاده میکند. این مقادیر یافت شده برای پارامترها، یک راه حل انعطافپذیر و بهترین و مناسبترین راه حل را در مورد references tracking به ما میدهد.
هنگامیکه سیگنالهای مناسب با enforcing signal bounds و یا با Tracking references sgnals انتخاب شد، پارامترهای تنظیمپذیر، تنظیم شدند و تنظیمات بهینهسازی را تعریف کردیم ما برای run کردن بهینهسازی آمادهایم.
بهینهسازی را با استفاده از Optimization>start در پنجره Signal constraint و یا کلیک کردن بر روی Start button که به صورت مثلث کوچک که در زیر Control panel که زیر منو قرار گرفته است، run میکنیم.
Simulink Response Optimization با کشیدن نمودار پاسخ اولیه به رنگ آبی در پنجره Signal constraint، شروع میشود. در طول بهینهسازی، پاسخهای میانی (Intermediate response) همچنین به رنگهای مختلف کشیده میشوند. پاسخ نهایی به رنگ سفید کشیده میشود. اگر پارامترهای نامعلوم در پروژه بهینهسازی وجود داشته باشند، سیگنالهای پاسخ نامعلوم به صورت خطوط نقطهچین و همچنین پاسخ اسمی به صورت خطوط یک تکه کشیده میشود.
Simulink Response Optimization مقادیر بدست آورده برای پارامترهای تنظیمپذیر را در Work space MATLAB تغییر میدهد و مقدار نهایی را Optimization progress window نمایش میدهد.
نکته بسیار مهمی که باید به آن توجه کنیم این است که بعد از بهینهسازی، مقادیر پارامترهای تنظیمپذیر، به مقادیر جدید بهینه شده تغییر میکند. این بدان معناست که اگر ما میخواهیم، بهینهسازی را دوباره run کنیم، Simulink Response Optimization این مقادیر تنظیم شده، را به عنوان مقادیر اولیه استفاده میکند، مگر اینکه ما مقادیر اولیه دیگری را در پنجره Tuned parameter تعریف کنیم. برای برگرداندن مقادیر بهینه نشده پارامترها Edit> undo optimize parameters را پنجره Signal constraint را انتخاب میکنیم. علاوه بر این نمودار سیگنالهای پاسخ و نیز مقادیر پارامترهای تنظیم شده، مقادیر عددی خروجی در پنجره optimization progress نشان داده میشود. فرم این خروجیها بستگی به الگوریتمی که برای بهینهسازی استفاده شده است، دارد.
- تنظیم نتایج شبیهسازی:
برای تنظیم نتایج شبیهسازی، چندین گزینه را باید تنظیم کنیم. این گزینهها شامل الگوریتم بهینهسازی و Telorance الگوریتمهای استفاده شده، میباشند. برای تنظیم پارامترهای بهینهسازی optimization>optimization option در پنجره Signal constraint را انتخاب میکنیم با این کار option dialog box باز میشود.
نکته بسیار مهمی که باید به آن توجه شود این است که اگر بهینهسازی fail شد یک راه حل مناسب برای برطرف کردن این مشکل این است که Gradient-type را به Refined تغییر دهیم.
- انتخاب روشهای بهینهسازی:
Algorithm و Model size هر دو ، Optimization method را تعریف میکنند. در Option dialog box از پنل optimization option استفاده میکنیم تا Algorithm و Model size را تنظیم کنیم.
برای پارامتر Algorithm سه گزینه وجود دارد:
- Gradient descent : Simulation از Optimization toolbox function fmincon بهینهسازی استفاده میکند.
- Pattern search :که از Genetic algorithm و Direct search toolbox function pattern search و یک روش advance direct search برای بهینهسازی استفاده میکند. این گزینه نیاز به Genetic algorithm و Direct search toolbox دارد.
- Simplex Search : از toolbox function fmin search و یک Direct search method برای بهینه کردن پاسخ استفاده میکند.
Simplex Search برای مسائل ساده، مفیدترین روش است و بعضی اوقات سریعتر از Gradient descent به صورت پیشفرض، پارامتر Model size تنظیم شده است. هنگامی که مدل خیلی بزرگ است و Gradient descent به عنوان الگوریتم بهینهسازی انتخاب میشوند، ما باید Model size را به Large scale تغییر دهیم تا سرعت محاسبه را افزایش دهیم.
- انتخاب گزینههای Optimization Termination :
از پنل Optimization Option برای تعریف زمان خاتمه بهینهسازی استفاده میکنیم. این پنل شامل گزینههای زیر است:
- Parameter tolerance : هنگامی که از الگوریتم Simplex search استفاده میکنیم، بهینهسازی هنگامی که مقادیر متوالی پارامتر به کمتر از Parameter tolerance تغییر کند، پایان خواهد یافت.
- Constraint telorance : این مقدار نشان دهنده ماکزیمم مقداری است که قیود میتوانند از آن تجاوز کنند وهمچنان همگرایی موفق داریم.
- Function telorance : اینگزینه فقط هنگامی مفید است که ما از گزینه Tracking reference signal استفاده میکنیم.
- : این گزینه، مقدار ماکزیمم تکرارها را نشان میدهد. بهینهسازی هنگامی که مقدار تکرار از این مقدار Maximum iteration تجاوز کند، پایان میپذیرد.
- انتخاب گزینههای اضافی بهینهسازی :
در انتهای پنل Optimization optiuoin یک گروه از گزینههای اضافی بهینهسازی وجود دارد. گزینههای اضافی برای بهینهسازی شامل :
- Display level : این گزینه فرم خروجیها در optimization progress window را تعریف میکند.
- Iterations : خروجی را بعد از هر تکرار نمایش میدهد.
- None : همه خروجیها را غیر فعال (خاموش) میکند.
- Notify : خروجی را فقط هنگامی که تابع همگرا نیست نشان میدهد.
- Restarts : در بسیاری بهینهسازیها، Hessian، ممکن است بدحالت شود و بهینهسازی همگرا نشود. در این موارد بعضی اوقات مقید است که بعد از اینکه بهینهسازی خاتمه یافت restart کنیم و از end-point (نقطه نهاییِ) قبلی به عنوان Starting point (نقطه شروع) برای بهینهسازی بعدی استفاده کنیم.
برای Restart کردن اتوماتیک بهینهسازی، در رشته مربوط به Restart، تعداد دفعاتی که میخواهیم بهینهسازی Restart شود، را وارد میکنیم.
- Gradient type : هنگامی که Gradient descent به عنوان الگوریتم استفاده میشود، Simulink Response Optimization، شیبها را بر مبنای متدهای مختلف (که پایانپذیر هستند) محاسبه میکند. متد Refine از متد Basic نویز کمتری دارد و قویتر است، اگر چه اغلب گرانتر است. این متد همچنین با مدلهای معلوم از قبیل مدلهای Simpower system کار نمیکند. اگر بهینهسازی fail شد یک اقدام خوب قبل از اینکهS lover را تغییر دهیم و Parameter bound را اضافه کنیم، این است که Gradient type را به refine تغییر دهیم.
– تنظیم شبیهسازی:
برای بهینه کردن سیگنالهای پاسخ Simulink Response Optimization، شبیهسازی مدل را run میکند. برای تنظیم گزینههای شبیهسازی (Simulation) باید Optimization> simulation option را در پنجره Signal constraint انتخاب کنیم. با این کار Options dialog box باز میشود، که شامل گزینههای زیر است.
- انتخاب زمان شبیهسازی:
به صورت پیش فرض start time و stop time به صورت اتوماتیک، با زمان شروع و خاتمه شبیهسازی مدل تنظیم میشود. برای تغییر زمانهای شروع و پایان برای پاسخ بهینهسازی آنها را در Simulation time وارد میکنیم.
- انتخاب Slover :
هنگامیکه شبیهسازی را run میکنیم، simUlink ، سیستم دینامیکی را با استفاده از چندین Slover حل میکند. ما میتوانیم با استفاده از پنل Solver option چندین گزینه Slover را تعریف کنیم. Slover میتواند Variable-step و یا Fixed-step باشد.
Variable-step solver خطا را در تلورانس تعریف شده (با تنظیم Step-size که Slover استفاده میکند) نگاه میدارد.
Fixed-step از یک Step-size ثابت استفاده میکند. هنگامی که حالت مدلمان خیلی سریع، تغییر میکند Variable-step solver اغلب از Fixed-step سریعتر است.
- Accelerating the Optimization :
Simulink Response Optimization به صورت اتوماتیک با simUlink Accelator کار میکند. (هنگامیکه اکثریت زمان بهینهسازی با Simulink Response Optimization سپری شده است)
با استفاده از simUlink Accelator، مقدار زمانی که صرف بهینهسازی میشود، کاهش مییابد.
در صورت نصب simUlink Accelator بر روی سیستم، ما میتوانیم Simulation>Accelator در پنجره مدل استفاده کنیم Simulink Response Optimization سپس با C-code که به وسیله simUlink Accelator تولید شده است، run میگردد.
برای گرفتن سرعت بیشتر از simUlink Accelator ، ما باید همه بلوکهای Scope و همچنین Function block MATLAB را برداریم و یا آنها را با FCN block جابهجا کنیم.
لازم به ذکر است که Accelator با Algebraic loop کار نمیکند.
فصل اول
- مقدمه :
موتورهای dc دارای مشخصه متغیر هستند و اکثراً در درایوهای با سرعت متغیر مورد استفاده قرار میگیرند. موتورهای dc قادر به ایجاد گشتاور نسبتاً زیادی در لحظه شروع کار میباشند و نیز کنترل سرعت را در رنج وسیعی امکانپذیر میسازند. در این نوع درایوها، روشهای کنترل سرعت معمولاً سادهتر و کم هزینهتر از درایوهای ac میباشند. موتورهای dc نقش مهمی را در درایوهای صنعتی جدید به عهده دارند. هر دو نوع موتورهای dc با تحریک جداگانه و سری، معمولاً در درایوهای با سرعت متغیر کاربرد دارند، اما موتورهای سری بیشتر برای کاربردهای حمل و نقلی استفاده میشوند. به خاطر وجود کموتاتورها، موتورهای dc در کاربردهای با سرعت خیلی بالا، چندان مناسب نمیباشند و نسبت به موتورهای ac به مراقبت بیشتری نیاز دارند. با توجه به پیشرفتهای جدید در زمینه تبدیل توان، روشهای کنترل و میکرو کامپیوترها، درایوهای موتورac، قابل رقابت با موتورهای dc گشتهاند. علیرغم اینکه روند آینده به کارگیری وسیع درایوها ac میباشد، درایوهای dc نیز هنوز در بسیاری از صنایع مورد استفاده قرار میگیرند و ممکن است چندین دهه طول کشد تا درایوهای dc نیز هنوز در بسیاری از صنایع مورد استفاده قرار میگیرند و ممکن است چندین دهه طول کشد تا درایوهای dc کاملاً توسط درایوهای ac جایگزین شوند.
یکسو کنندههای کنترل شده قادر به ایجاد ولتاژ خروجی dc متغیر از یک ولتاژ ac ثابت میباشند. در حالیکه چاپرها از یک ولتاژ dc ثابت، یک ولتاژ dc متغیر تولید میکنند. یکسوکنندههای کنترل شده و چاپرهای dc، به خاطر توانایی تأمین یک ولتاژ dc با تغییرات پیوسته، در زمینه وسایل یکسوکننده دیودی با یک چاپر همانند شکل ۱-۱ ب میباشد. درایوهای dc به طور کلی به سه نوع تقسیم میشوند:
- درایوهای تکفاز
- درایوهای سه فاز
- درایوهای چاپر
۲-۱ : مشخصه اصلی موتورهای dc:
در شکل ۲-۱، مدار معادل یک موتور dc با تحریک جداگانه نشان داده شده است. هنگامی که یک موتور با تحریک میدان تحریک میگردد و جریان آرمیچر در مدار آرمیچر برقرار میگردد، موتور یک نیروی محرکه بر عکس و گشتاوری برای موازنه با گشتاور بار در یک سرعت مشخص، ایجاد مینماید. جریان میدان یک موتور با تحریک جداگانه از جریان آرمیچر مستقل است و تغییرات جریان آرمیچر هیچگونه اثری بر جریان میدان نخواهد داشت. جریان میدان معمولاً کمتر از جریان آرمیچر میباشد.
معادلات توصیف کننده مشخصه یک موتور با تحریک جداگانه را میتوان با توجه به شکل ۲-۱ تعیین کرد.
جریان میدان لحظهای از رابطه زیر به دست میآید:
جریان لحظهای آرمیچر از رابطه زیر به دست میآید:
نیروی ضد محرکه موتور، که با نام ولتاژ سرعت نیز شناخته میشود، به صورت زیر بیان میگردد:
گشتاور ایجاد شده توسط موتور برابر است با :
گشتاور ایجاد شده باید برابر گشتاور بار باشد:
که در آن
= سرعت موتور بر حسب
= ثابت اصطکاک ویسکوز
= ثابت ولتاژ
= ثابت گشتاور
= اندوکتانس مدار آرمیچر H
= اندوکتانس مدار میدان H
= مقاومت مدار آرمیچر
= مقاومت مدار میدان
= گشتاور بار
تحت شرایط حالت پایدار، مشتقات زمانی در این روابط صفر است و مقادیر متوسط حالت پایدار کمیتها عبارتند از:
(۱-۱)
(۲-۱)
(۳-۱)
(۴-۱)
توان ایجاد شده برابر است با :
رابطه بین جریان میدان و emf بر عکس به خاطر اشباع مغناطیسی، یک رابطه غیر خطی است. این رابطه که در شکل ۳-۱ نشان داده شده است با نام مشخصه مغناطیسی موتور شناخته میشود. از رابطه ۳-۱ میتوان سرعت یک موتور با تحریک جداگانه را بدست آورد.
(۷-۱)
از رابطه (۷-۱) متوجه میشویم که سرعت موتور را میتوان به روشهای زیر تغییر داد: ۱) با کنترل ولتاژ آرمیچر، که به نام کنترل ولتاژ شناخته میشود. ۲) با کنترل جریان میدان که به نام کنترل میدان شناخته میشود، یا ۳) با نیاز گشتاور، که متناظر است با یک جریان آرمیچر، ، برای یک جریان میدان ثابت، . سرعت، که از روی ولتاژ نامی آرمیچر، جریان نامی میدان، و جریان نامی آرمیچر بدست میآید به نام سرعت پایه شناخته میشود. در عمل برای سرعتهای کمتر از سرعت پایه، جریان آرمیچر و جریانهای میدان جهت ایجاد گشتاور مورد نیاز، ثابت نگه داشته میشود و ولتاژ آرمیچر ، برای کنترل سرعت، تغییر داده میشود. در سرعتهای بیشتر از سرعت پایه، ولتاژ آرمیجر در مقدار نامی نگه داشته میشود. و جریان میدان برای کنترل سرعت، تغییر داده میشود. گرچه توان ایجاد شده توسط موتور (=سرعت*گشتاور) ثابت باقی خواهد ماند. شکل (۴-۱) مشخصات گشتاور، توان، جریان آرمیچر و جریان میدان را به ازای سرعت نشان میدهد.
۳-۱ : حالتهای کاری:
در کاربردهای با سرعت متغیر یک موتور DC میتواند در یک حالت یا بیشتر کار کند: حالت موتوری، ترمز، معکوس، ترمز دینامیکی، پلاکینگ و چهار ربعی.
- حالت موتوری: آرایش حالت موتوری در شکل ۵-۱٫ الف نشان داده شده است. در این حالت نیروی ضد محرکه از ولتاژ منبع کمتر است. جریانهای میدان و آرمیچر هر دو مثبت هستند. موتور گشتاور مورد نیاز بار را تأمین میکند.
- ترمز معکوس: آرایش ترمز معکوس در شکل ۵-۱ ب نشان داده شده است. موتور مانند یک مولد عمل میکند و یک ولتاژ القایی ایجاد مینماید. میبایست از ولتاژ تغذیه بزرگتر باشد. در این حالت جریان آرمیچر منفی است، اما جریان میدان مثبت است. انرژی جنبشی موتور به منبع بر میگردد. یک موتور سری اغلب مانند یک ژنراتور با تحریک خودکار متصل میگردد. برای تحریک خودکار لازم است جریان میدان، شار پس مانده را تقویت نماید. معمولاً این عمل بوسیله معکوس کردن سرهای آرمیچر یا میدان صورت میگیرد.
- ترمز دینامیکی: آرایش ترمز دینامیکی نشان داده شده در شکل ۵-۱ج مشابه آرایش ترمزی معکوس میباشد، با این تفاوت که ولتاژ منبع با مقاومت ترمز جایگزین شده است. انرزی جنبشی موتور در تلف میشود.
- پلاکینگ: پلاکینگ نوعی ترمز است. اتصالات این حالت در شکل ۵-۱ د نشان داده شده است. سرهای آرمیچر هنگام کار معکوس میشوند. ولتاژ تغذیه و ولتاژ القایی در یک جهت عمل میکنند. جریان آرمیچر معکوس میشود و در نتیجه یک گشتاور ترمزی تولید مینماید. جریان میدان مثبت است.
- چهارربعی: شکل ۶-۱ قطبیت ولتاژ منبع ، نیروی ضد محرکه و جریان آرمیچر، را برای یک موتور با تحریک جداگانه نشان میدهد. در حالت موتوری مستقیم (ربع اول)، مقادیر ، ، همگی مثبت هستند. گشتاور سرعت نیز در این ربع مثبت هستند.
در حین ترمز مستقیم (ربع دوم) موتور در جهت مستقیم کار میکند و نیروی محرکه القایی همچنان مثبت خواهد بود. برای منفی شدن گشتاور و معکوس جهت انتقال انرژی، جریان آرمیچر میبایست منفی باشد. ولتاژ (ولتاژ منبع) میبایست کمتر از نگه داشته شود.
در حالت موتوری معکوس (ربع سوم)، مقادیر ، ، همگی منفی هستند. گشتاور و سرعت نیز در این ربع منفی هستند. برای منفی نگه داشتن گشتاور و جاری شدن انرژی از منبع به موتور، نیروی ضد محرکه ، میبایست در شرط صدق نماید. قطبیت را میتوان با تغییر جهت میدان یا با معکوس شدن سرهای آرمیچر، معکوس نمود.
در حین ترمز معکوس (ربع چهارم)، موتور در جهت معکوس کار میکند. و همچنان منفی خواهد بود. برای مثبت بودن گشتاور و انتقال انرژی از موتور به منبع، جریان آرمیچر میبایست مثبت باشد. نیروی محرکه القایی ، باید در شرط صدق نماید.
۴-۱ درایوهای تکفاز :
اگر مدار آرمیچر یک موتور dc به خروجی یک یکسو کننده کنترل شده تکفاز متصل گردد، با تغییر زاویه تأخیر مبدل میتوان ولتاژ آرمیچر را تغییر داد. از مبدلهای ac به dc با کموتاسیون اجباری میتوان برای بهبود ضریب توان و کاهش هارمونیکها استفاده کرد. در شکل ۷-۱ مدار ساده یک موتور با تحریک جداگانه تغذیه شونده با مبدل تک فاز نشان داده شده است. در زاویه تأخیر کم، ممکن است جریان آرمیچر پیوسته نباشد و این باعث افزایش تلفات در موتور میگردد. معمولاً برای کاهش جریان ریپل تا حد قابل قبول، یک سلف هموار کننده به طور سری با مدار آرمیچر قرار داده میشود. همچنین برای کنترل جریان میدان توسط ایجاد تغییر در زاویه تأإیر ، یک مبدل در مدار میدان قرار داده میشود. برای به کار گیری موتور در یک حالت خاص، غالباً از کنتاکتورها برای معکوس کردن مدار آرمیچر مشابه شکل ۸-۱ الف یا مدار میدان مشابه ۸-۱ ب استفاده میشود. برای اجتناب از پالسهای ولتاژ القایی، عمل معکوس کردن مدار آرمیچر و یا میدان، در هنگامی که جریان آرمیچر صفر است، انجام میگیرد. زاویه تأخیر (یا آتش) معمولاً طوری تنظیم میشود که جریان صفر گردد و علاوه بر این زمان میرایی برابر با ۲ الی ۱۰ میلی ثانیه در نظر گرفته میشود. تا از صفر شدن جریان آرمیچر مطئمن شویم. به دلیل ثابت زمانی نسبتاً بزرگ سیمپیچی میدان، معکوس شدن میدان به زمان بیشتری نیاز دارد. از مبدل نیمه یا کامل میتوان برای تغییر ولتاژ میدان استفاده کرد. البته استفاده از مبدل کامل ارجحیت دارد. با توجه به توانایی معکوس کردن ولتاژ، مبدل کامل جریان میدان را سریعتر از مبدل نیمه کاهش میدهد. بسته به نوع مبدلهای تک فاز، درایوهای تک فاز به انواع زیر تقسیم میگردند:
- درایوهای با مبدل نیم موج تک فاز
- درایوهای با مبدل نیمه تک فاز
- درایوهای با مبدل کامل تک فاز
- درایوهای با مبدل دوگانه تک فاز
- درایوهای با مبدل نیم موج تک فاز
شکل ۹-۱ الف نمایانگر یک موتور dc است که توسط یک مبدل نیمه موج تکفاز تغذیه میشود. جریان آرمیچر معمولاً نا پیوسته میباشد، مگر اینکه یا سلف خیل یبزرگ در مدار آرمیچر قرار داده شود. همیشه یک دیود هرزگرد برای بار موتور dc مـــورد نیاز است و این همان طور که در شکل ۹-۱ ب نشان داده شده است، یک درایو یک ربعی است. کاربرد این درایو تا سطح توان برابر نیم کیلو وات محدود میشود. شکل ۹-۱ ج شکل موجها را برای یک بار شدیداً سلفی نشان میدهد. مبدل مدار میدان میتواند یک مبدل نیمه باشد. یک مبدل نیم موج در مدار میدان، به خاطر بالا بودن مقدار ریپل جریان تحریک میدان، تلفات مغناطیسی موتور را افزایش می دهد.
برای یک مبدل نیم موج تک فاز در مدار آرمیچر از رابه ۸-۱ ولتاژ متوسط آرمیچر به دست میآید.
(۸-۱)
که در رابطه بالا ولتاژ پیک منبع ac میباشد. با یک مبدل نیمه در مدار میدان، از رابطه ۹-۱ ولتاژ متوسط به صورت زیر به دست میآید.
(۹-۱)
۲-۴-۱ درایوهای با مبدل نیمه تک فاز
در شکل ۱۰-۱ الف، یکمبدل نیمه تک فاز مدار آرمیچر را تغذیه میکند. همان طور که در شکل ۱۰-۱ ب نشان داده شده است، یک درایو یک ربعی است که محدوده کار آن تا kw15 میباشد. مبدل در مدار میدان میتواند یک مبدل نیمه باشد. شکل موجهای جریان برای یک بار شدیداً سلفی در شکل ۱۰-۱ ج نشان داده شده است با یک مبدل نیمه تک فاز در مدار آرمیچر از رابطه ۱۰-۱ ولتاژ متوسط آرمیچر برابر میشود با :
(۱۰-۱)
با یک مبدل نمیه تک فاز در مدار میدان از رابطه ۱۱-۱ ولتاژ متوسط میدان برابر میشود با
(۱۱-۱)
۳-۴-۱ درایوهای با مبدل کامل تک فاز
ولتاژ آرمیچر با استفاده از یک مبدل تمام موج تک فاز همان طور که در شکل ۱۱-۱ الف نشان داده شده است، تغییر داده میشود. این درایو همان طور که در شکل ۱۱-۱ ب نشان داده شده، دو ربعی است و قابلیت کار تا توان kw15 را دارا میباشد. مبدل آرمیچر ولتاژهای یا را ایجاد نموده و اجازه کارکرد در ربع اول و چهارم را میدهد. در طی حالت مولدی برای معکوس کردن جهت انتقال توان، نیروی ضد محرکه موتور را میتوان با معکوس کردن تحریک میدان، معکوس کرد. مبدل مدار میدان میتواندیک مبدل از نوع نیمه یا کامل و یا حتی دوگانه باشد. معکوس شدن آرمیچر یا میدان کاردر ربعهای دوم سوم را امکانپذیر میسازد. شکل موجهای جریان برای یک بار شدیداً سلفی، در شکل ۱۱-۱ ج برای عملکرد توانی نشان داده شده است. با قرار دادن یک مبدل تمام موج تک فاز در مدار آرمیچر، از رابطه ۱۲-۱ مقدار متوسط ولتاژ آرمیچر به صورت زیر بدست میآید.
(۱۲-۱)
با وجود یک مبدل کامل تک فاز در مدار میدان، از رابطه ۱۳-۱ مقدار ولتاژ میدان به به دست میآید.
(۱۳-۱)
۴-۴-۱ درایوهای مبدل دو گانه تک فاز
در این حالت دو مبدل تمام موج تک فاز مانند شکل ۱۲-۱ به هم بسته شدهاند. یا مبدل شماره ۱ برای تأمین ولتاژ مثبت آرمیچر، ، و یا مبدل شماره ۲ برای تأمین ولتاژ منفی آرمیچر، عمل میکند. مبدل شماره ۱ کارکرد در ربع اول و چهارم و مبدل شماره ۲ نیز امکان کار در ربع دوم و سوم را ایجاد مینماید. این یک درایو چهارربعی است واجازه کار در چهار حالت را میدهد: تواندهی مستقیم، ترمز مستقیم (مولدی) تواندهی معکوس و ترمز معکوس(مولدی). محدوده عملکرد این درایو برای کاربردهای تا kw15 است. مبدل میتواند یک مبدل نیم موج یا تمام موج یا دوگانه باشد.
اگر مبدل ۱ با زاویه تأخیر برابر عمل کند، از رابطه ۱۴-۱ ولتاژ آرمیچر بدست میآید.
(۱۴-۱)
اگر مبدل ۲ با زاویه تأخیر برابر عمل کند، از رابطه ۱۵-۱ ولتاژ آرمیچر بدست میآید.
(۱۵-۱)
که در آن میباشد. با وجود یک مبدل کامل در مدار میدان، از رابطه ۱۶-۱ ولتاژ میدان به دست میآید:
(۱۶-۱)
۵-۱ درایوهای سه فاز
در این نوعت درایو، مدار آرمیچر به خروجی یک یکسوکننده کنترل شده سه فاز یا یک مبدل ac به dc سه فاز با کموتاسیون اجباری متصل شده است. درایوهای سه فاز در کاربردهایی که نیاز به توان زیادی دارند (تا چندین مگاوات) مورد استفاده میگیرند. فرکانس ریپل ولتاژ آرمیچر بیشتر از درایوهای تک فاز میباشد و در نتیجه در مدار آرمیچر نیاز به اندوکتانس کمتری جهت کاهش جریان ریپل آرمیچر میباشد. جریان آرمیچر غالباً پیوسته است و بنابراین کارآیی موتور در مقایسه با درایوهای تک فاز بهتر میباشد. همانند درایوهای تک فاز، درایوهای سه فاز را نیز میتوان به انواع زیر تقسیم کرد:
- درایوهای سه فاز با مبدل نیم موج
- درایوهای سه فاز با نیمه مبدل
- درایوهای سه فاز با مبدل کامل
- درایوهای سه فاز با مبدل دوگانه
۱-۵-۱ درایوهای سه فاز با مبدل نیم مو ج
یک درایو موتور dc تغذیه شونده با مبدل نیم موج سه فاز در یک ربع کار میکند و میتواند در کاربردهای تا توان kw40 استفاده شود. مبدل میدان میتواند یک مبدل نمیه سه فاز یا تک فاز باشد. این درایو معمولاً درکاربردهای صنعتی به دلیل اینکهمنبع ac آن شامل مؤلفههای dc می باشد، مورد استفاده قرار نمیگیرد.
با یک مبدل نیم موج سه فاز در مدار آرمیچر از رابطه ۱۷-۱ ولتاژ آرمیچر به دست میآید.
(۱۷-۱)
که در آن ، پیک ولتاژ فاز یک مبنع ac سه فاز با اتصال ستاره است. با داشتن یک مبدل نیمه سه فاز در مدار میدان،از رابطه ۱۸-۱ ولتاژ میدان به صورت زیر به دست میآید.
(۱۸-۱)
۲-۵-۱ درایوهای مبدل نیمه سه فاز
یک درایو تغذیه شونده با مبدل نیمه سه فاز، یک درایو یک ربعی بدون معکوس شوندگی میدان است و محدوده کار آن تا توان kw115 است. مبدل میدان نیز باید یک مبدل نیمه سه فاز یا تک فاز باشد.
با وجود یک مبدل نیمه سه فاز در مدار آرمیچر، از رابطه ۱۹-۱ ولتاژ آرمیچر به صورت زیر بدست میآید.
(۱۹-۱)
با یک مبدل نیمه سه فاز در مدار میدان، از رابطه ۲۰-۱ ولتاژ میدان به دست میآید:
(۲۰-۱)
۳-۵-۱ درایوهای با مبدل کامل سه فاز
درایو با مبدل تمام موج سه فاز یک درایو دو ربعی بدون هر گونه معکوس شوندگی میدان است و محدوده کار آن تا کاربردهای با توان kw1500 میبتاشد. طی حالت مولدی برای معکوس کردن جهت انتقال توان، نیروی ضد محرکه موتور به وسیله معکوس کردن تحریک میدان، معکوس میشود. مبدل در مدار میدان باید یک مبدل کامل سه فاز یا تک فاز باشد.
با یک مبدل تمام موج سه فاز در مدار آرمیچر، از رابطه ۲۱-۱ ولتاژ آرمیچر به دست میآید.
(۲۱-۱)
با یک مبدل کامل سه فاز در مدار میدانف از رابطه ۲۲-۱ ولتاژ میدان مطابق رابطه زیر بدست میآید:
(۲۲-۱)
۴-۵-۱ درایوهای با مبدل دوگانه سه فاز
در این نوع درایو، دو مبدل تمام موج سه فاز با آرایش مشابه شکل ۱۲-۱ الف به یکدیگر متصل شدهاند یا مبدل شماره۱، جهت تأمین ولتاژ مثبت آرمیچر، و یا مبدل شماره ۲ برای تأمین ولتاژ منفی عمل میکند. این درایو در چهار ربع کار میکند و محدوده کار آن تا کاربردهای با توان kw1500 است.
مشابه درایوهای تکفاز مبدل میدان میتواند یک مبدل نیمه یا یک مبدل کامل باشد. اگر مبدل شماره ۱ با زاویه تأخیر عمل کند، از رابطه ۲۳-۱ مقدار متوسط ولتاژ آرمیچر از رابطه زیر به دست میآید:
(۲۳-۱)
اگر مبدل دوم با زاویه تأخیر عمل کند، از رابطه ۲۴-۱ مقدار متوسط ولتاژ آرمیچر طبق رابطه زیر به دست میآید:
(۲۴-۱)
با یک مبدل کامل سه فاز در مدار میدان، از رابطه ۲۵-۱ مقدار متوسط ولتاژ میدان به دست میآید.
(۲۵-۱)
۶-۱ کنترل حلقه بسته درایوهای dc
سرعت موتورهای dc با گشتاور بار تغییر میکند. برای به دست آوردن یک سرعت ثابت، ولتاژ آرمیچر (و یا میدان) میبایست به طور مداوم با تغییر زاویه تأخیر مبدلهای ac به dc و یا سیکل کاری چاپرهای dc تغییر نماید. در سیستمهای درایو عملی لازم است درایو را در یک گشتاور ثابت یا توانت ثابت به کار گرفت، به علاوه شتابدهی و کاهش شتاب کنترل شده مورد نیاز است. اکثر درایوهای صنعتی به صورت سیستمهای فیدبک حلقه بسته عمل میکنند. یک سیستم کنترلی حلقه بسته مزایایی چون دقت بالا، پاسخ دینامیکی و سریع و کاهش اثرات اغتشاشهای بار و غیر خطی شدنهای سیستم را دارا میباشد.
نمودار یک درایو dc حلقه بسته با تحریک جداگانه و با تغذیه مبدلی در شکل ۱۳-۱ نشان داده شده است. اگر سرعت موتور به دلیل به کارگیری گشتاور بار اضافی، کاهش یابد، خطای سرعت افزایش مییابد. کنترل کننده سرعت با یک سیگنال کنترل افزایش یافته ، تغییر زاویه تأخیر یا سیک کاری مبدل و افزایش ولتاژ آرمیچر موتور پاسخ میدهد. ولتاژ افزایش یافته آرمیچر، گشتاور بیشتری برای بارگرداندن سرعت موتور به مقدار اولیه ایجاد مینماید. درایو معمولاً از یک دره گذرا عبور میکند، تا اینکه گشتاور ایجاد شده با گشتاور بار برابر شود.
۱-۶-۱ تابع انتقال حلقه باز
ویژگیهای حالت پایدار درایوهای dc که در بخشهای قبل مورد بررسی قرار گرفت، دارای اهمیت زیادی در انتخاب درایوهای dc است ولی هنگامی که از درایو کنترل حلقه بسته استفاده میشود، کافی میباشد و آگاهی از رفتار دینامیکی که معمولاً به صورت تابع انتقال بیان میشود، نیز حائز اهمیت است.
آرایش یک درایو موتور dc تحریک جداگانه با تغذیه مبدلی و کنترل حلقه باز در شکل ۱۴-۱ نشان داده شده است. سرعت موتور با تنظیم ولتاژ مبنا (با کنترل) تنظیم شود. با در نظر گرفتن یک مبدل توان خطی با بهره ، ولتاژ آرمیچر موتور برابر میشود با
(۱۷-۱)
اگر جریان میدان موتور و ثابت نیروی ضد محرکه، در حین هر اغتشاش گذرایی ثابت بمانند، معادلات سیستم به شرح زیر خواهند بود.
(۱۸-۱)
(۱۹-۱)
(۲۰-۱)
(۲۱-۱)
رفتار گذرا را میتوان با تغییر معادلات سیستم به تبدیل لاپلاس با شرایط اولیه صفر، آنالیز نمود. از تبدیل معادلات ۱۷-۱، ۱۹-۱، ۲۱-۱ نتیجه میگیریم.
(۲۲-۱)
(۲۳-۱)
(۲۴-۱)
از رابطه ۲۳-۱ جریان آرمیچر برابر میشود با
(۲۵-۱)
(۲۶-۱)
که ثابت زمانی مدار آرمیچر موتور نامیده میشود. از رابطه ۲۴-۱ سرعت موتور برابر است با :
(۲۷-۱)
(۲۸-۱)
که ثابت زمانی مکانیکی موتور نامیده میشود. از روابط ۲۲-۱، ۲۶-۱، ۲۶-۱ میتوان برای رسم نمودار حلقه باز، همان طور که در شکل ۱۵-۱ نشان داده شده است، استفاده کرد. دو اغتشاش ممکن ولتاژ کنترل و گشتاور بار هستند. پاسخهای حالت پایدار را میتوان از ترکیب پاسخهای جداگانه به و تعیین کرد.
پاسخ ناشی از یک تغییر پلهای در ولتاژ مبنا، با صفر قرار دادن به دست میآید. از شکل ۱۵-۱ میتوانیم پاسخ سرعت ناشی از ولتاژ مبنا را به صورت زیر به دست میآوریم.
(۲۹-۱)
پاسخ ناشی از تغییر در گشتاور بار، ، با صفر قرار دادن به دست میآید. نمودار یک تغییر پله در اغتشاش گشتاور بار در شکل ۱۶-۱ نشان داده شده است.
(۳۰-۱)
با استفاده از تئوری مقدار نهایی، رابطه حالت پایدار برای تغییر در سرعت، ، ناشی از یک تغییر پله در ولتاژ کنترل و یک تغییر پله درگشتاور بار را میتوان به ترتیب از رابطه ۲۹-۱ و ۳۰-۱ با جایگزین کردن s=0 به دست آورد.
(۳۱-۱)
(۳۲-۱)
۲-۶-۱ تابع انتقال حلقه بسته
پس از آنکه مدلهای موتور شناخته شدند، مسیرهای فیدبک را میتوان اضافه کرد تا پاسخ خروجی مطلوب به دست آید، برایتغییر در آرایش حلقه باز نشان داده شده در شکل ۱۴-۱ به یک سیستم حلقه بسته، میبایست یک حسگر سرعت به محور خروجی متصل کرد. خروجی حسگر که متناسب با سرعت استف با ضریب تقویت شده و با ولتاژ مبنا مقایسه میگردد تا ولتاژ خطا به دست آید.
نمودار کامل در شکل ۱۹-۱ نشان داده شده است.
پاسخ بله حلقه بسته ناشی از تغییر در ولتاژ مبنا را میتوان از شکل ۱۹-۱ با به دست آورد. تابع انتقال برابر میشود با :
(۳۳-۱)
پاسخ ناشی از تغییر در گشتاور بار نیز از شکل ۱۹-۱ با صفر قرار دادن به دست میآید. تابع انتقال برابر میشود با :
(۳۴-۱)
با استفاده از تئوری مقدار نهایی، تغییر حالت پایدار در سرعت ، ناشی از تغییر پله در ولتاژ کنترل و تغییر پله در گشتاور را میتوان به ترتیب از رابطه ۳۳-۱ و ۳۴-۱ با قرار دادن s=0 به دست آورد :
(۳۵-۱)
(۳۶-۱)
شکل ۱۹-۱ فقط از یک فیدبک سرعت استفاده میکند، درعمل لازم است که موتور در سرعت مطلوب کار کند، اما باید گشتاور بار را که به جریان آرمیچر بستگی دارد، نیز تأمین کند. هنگامی که موتور در سرعت به خصوص کار، میکند، اگر باری به طور ناگهانی به آن اعمال شود، سرعت کم شده، و مدت زمانی طول میکشد تا موتور دوباره به سرعت مطلوب برسد. یک فیدبک سرعت با حلقه جریان داخلی مانند شکل ۲۰-۱ پاسخ سریعتری به هر گونه اغتشاشی در دستور سرعت، گشتاور بار و منبع ولتاژ فراهم میکند.
حلقه جریان برای مقابله با نیاز گشتاور ناگهانی تحت شرایط گذرا، به کار میرود. خروجی کنترلکننده سرعت به محدود کننده جریان اعمال میشود، که مبنای جریان را برای حلقه جریان تنظیم میکند. جریان آرمیچر توسط یک حسگر سنجیده شده و معمولاً با یک فیلتر اکتیو جهت از بین بردن ریپل فیلتر میشود و با جریان مبنا مقایسه میشود. جریان خطا توسط کنترلکننده، جریانی، که خروجی آن، زاویه آتش مبدل را تنظیم کرده و سرعت موتور را به مقدار مطلوب میرساند، پردازش میشود.
هر گونه خطای سرعت مثبت ناشی از دستور سرعت و یا نیاز گشتاور باعث تولید یک جریان مبنای زیاد میشود. موتور شتاب گرفته تا خطای سرعت را تصحیح کند و نهایتاً در یک جدید تنظیم میشود که گشتاور موتور را برابر با گشتاور بار میسازد و در نتیجه خطای سرعت به صفر نزدیک میشود. برای هر گونه خطای سرعت مثبت بزرگ، محدودکننده جریان به اشباع رفته و مقدار جریان مبنا را به مقدار حداکثر محدود میکند. سپس خطای سرعت در ماکزیمم مقدار جریان آرمیچر مجاز، تصحیح میگردد تا اینکه خطای سرعت کوچک شده و محدود کننده جریان از اشباع خارج شود. معمولاً خطای سرعت با کمتر از مقدار مجاز تصحیح میگردد.
معمولاً کنترل سرعت از صفر تا سرع پایه، در ماکزیمم میدان به وسیله کنترل ولتاژ آرمیچر انجام میشود و کنترل در سرعتهای بیشتر از سرعت پایه با تضعیف میدان در ولتاژ نامی آرمیچر انجام میشود. در حلقه کنترل میدان، نیروی ضد محرکه، ، با ولتاژ مبنا مقایسه میشود، که معمولاً بین ۰٫۸۵ تا ۰٫۹۵ ولتاژ نامی آرمیچر میباشد. برای سرعتهای کمتر از سرعت پایه، خطای میدان زیاد بوده و کنترل کننده میدان به اشباع میرود، بدین جهت ماکزیمم ولتاژ و جریان میدان اعمال میشود.
وقتی سرعت نزدیک دستور سرعت بالاتر از سرعت پایه است، تقریباً نزدیک به مقدار نامی بوده و کنترل کننده میدان از اشباع بیرون میآید. برای دستور سرعت بالاتر از سرعت پایه، خطای سرعت سبب میشود مقدار بیشتر گردد. موتور شتاب گرفته، نیروی ضد محرکه افزایش یافته و خطای میدان کاهش مییابد. جریان میدان سپس ککاهش مییابد و سرعت موتور به افزایش یافتن ادامه میدهد تا اینکه سرعت موتور به سرعت مطلوب برسد. بنابراین کنترل سرعت در مقادیر بیش از سرعت پایه با تضعیف میدان هنگامی که ولتاژ ترمینال آرمیچر نزدیک به مقدار نامی نگه داشته میشود، انجام میپذیرد. در حالت تضعیف میدان، درایو به خاطر ثابت زمانی بزرگ میدان، خیلی آهسته پاسخ میدهد. معمولاً یک مبدل کامل در میدان به کار گرفته میشود. زیرا این مبدل قابلیت معکوس کردن ولتاژ را دارد، در نتیجه جریان میدان سریعتر از حالت با مبدل نیمه کاهش مییابد.
فصل دوم
- مقدمه :
یک محرک رایج در سیستمهای کنترل، موتور dc است که یک حرکت دورانی را به وجود میآورد. مدار الکتریکی آرمیچر و دیاگرام بدون بدنه روتور در شکل زیر نشان داده شده است.
برای مثال ، ما مقادیر زیر را برای پارامترهای فیزیکی فرض خواهیم کرد :
- مقدار اینرسی روتور
- نسبت میرایی سیستم مکانیکی
- ثابت نیروی موتوری
- مقاومت الکتریکی
- مقاومت القایی
- ولتاژ ورودی (V) = ولتاژ منبع
- خروجی = موقعیت شفت
گشتاور موتور (T) با ضریب ثابت kt به جریان آرمیچر (i) مرتبط میشود . emf برگشتی (e) به وسیله معادلات زیر به سرعت دورانی مربوط میشود :
در سیستمهای SI (که ما استفاده میکنیم) kt (ثابت آرمیچر) یا ke (ثابت موتور) مساوی است.
۲-۲ ساخت مدل :
این سیستم بوسیله جمع گشتاورهای عمل کننده روی روتور و انتگرالگیری از شتاب (به منظور بدست آوردن سرعت) مدل میشود. همچنین قوانین “kirchoff” برای مدار آرمیچر به کار گرفته میشوند.
- simUlink را باز کنید و یک پنجره مدل جدید را باز کنید.
- ابتدا ما انتگرالهای شتاب دورانی و آهنگ تغییرات جریان آرمیچر را مدل خواهیم کرد.
- یک بلوک انتگرالگیری از (Linear block library) قرار میدهیم و خطوط را از ترمینالهای ورودی و خروجیاش رسم میکنیم.
- خط ورودی را «» و خط خروجی را «» همان طور که در شکل زیر نشان داده شده است، نامگذاری میکنیم.
- یک بلوک انتگرالگیری دیگر زیر بلوک قبلی قرار میدهیم و خطوط را از ترمینالهای ورودی و خروجیاش رسم میکنیم.
- خط ورودی را «» و خط خروجی را «i» مینامیم.
سپس ما دو قانون Newton و kirchoff را مدل میکنیم. این قوانین در سیستم موتور معادلات زیر را میدهند:
شتاب زاویهای برابر با حاصلضرب در جمع دو ترم (یکی با علامت مثبت و دیگری با علامت منفی) است. به طور مشابه مشتق جریان مساوی با حاصلضرب در جمع سه ترم (یکی با علامت مثبت و دو تا با علامت منفی) است.
– دو بلوک Gain (از Linear block library) برای هر کدام از انتگرالها قرار میدهیم. همچنین دو بلوک sum در مدل قرار دهیم.
- مقدار یکی از بلوکها را به تغییر میدهیم و نام آن را به “inertial” تغییر میدهیم.
- مقدار بلوک دیگری را به تغییر میدهیم و نام آن را به “Inductance” تغییر میدهیم.
- علامتهای بلوکهای sum را به صورت «- +» و «-+-» تغییر میدهیم.
حالا ما گشتاورهایی که در معادلات نیوتن وجود دارند را اضافه میکنیم. ابتدا ما گشتاور میرا را اضافه میکنیم.
- یک بلوک Gain زیر بلوک «inertia» قرار میدهیم.
- مقدار Gain را به «b» تغییر میدهیم و آن را «damping» مینامیم.
- خروجی انتگرالگیری زاویهای را به ورودی بلوک damping gain وصل میکنیم.
- یک خط از خروجی damping gain به ورودی منفی بلوک «rotational Sum» میکشیم.
حالا ما گشتاور آرمیچر را اضافه میکنیم.
- یک بلوک gain را به ورودی مثبت بلوک «rotational Sum» وصل میکنیم.
- مقدار آن را به «k» تغییر میدهیم و آن را در «kt» مینامیم.
- یک خط از انتگرالگیر جریان به بلوک «kt gain» وصل میکنیم.
حالا ما ترمهای ولتاژ که در معادلات kirchoff ظاهر میشوند. را اضافه میکنیم. ابتدا ما افت ولتاژ مقاومت هسته را اضافه میکنیم.
- یک بلوک gain بالای inductance block قرار میدهیم.
- مقدار آن را به «R» تغییر میدهیم و آن را «Resistance» مینامیم.
- خروجی انتگرالگیر جریان و ورودی بلوک «Resistance gain» را به هم وصل میکنیم.
- از خروجی «Resistance gain» به ورودی بالایی منفی «Sum block» جریان وصل میکنیم.
- حالا ما emf برگشتی از موتور را اضافه میکنیم.
- یک بلوک gain قرار میدهیم و آن را به ورودی منفی دیگر بلوک Sum جریان با یک خط وصل میکنیم.
- مقدار آن را به «k» تغییر میدهیم و آن را «ke» مینامیم.
- خروجی انتگرالگیر زاویهای و بلوک «ke gain» را به هم وصل میکنیم.
سومین ترم ولتاژ در معادله kirchoff ورودی کنترل V میباشد. ما یک ورودی step قرار خواهیم داد.
- یک بلوک step (از Source block library) قرار میدهیم و آن را با یک خط به ورودی مثبت بلوک Sum جریان وصل میکنیم.
- برای دیدن سرعت خروجی یک Scope (از sink block library) به خروجی انتگرالگیری زاویهای وصل میکنیم.
به منظور ایجاد یک پله واحد مناسب ورودی در t=0 ، step time را صفر تنظیم میکنیم.
۳-۲ پاسخ حلقه باز
برای شبیهسازی این سیستم، ابتدا زمان شبیهسازی مناسب باید تعیین شود. «Parameters» را از “Simulation menu” انتخاب میکنیم و در فیلد “Stop time” عدد «۳» را وارد میکنیم. «۳» ثانیه زمان کافی برای دیدن پاسخ حلقه باز میباشد. پارامترهای فیزیکی حالا باید تنظیم شوند. مقادیر زیر را در prompt MATLAB ، run میکنیم:
J= 0.01;
b=0.1;
k=0.01;
R=1;
L=0.5;
Simulation را شروع میکنیم. هنگامی که Simulation پایان یافت، با استفاده از Scope سرعت را میبینیم. خروجی به صورت زیر است.
۳-۳ قرار دادن یک مدل خطی در MATLAB :
مدل خطی سیستم (به صورت فضای حالت یا تابع تبدیل) از یک مدل simUlink به MATLAB میتواند استخراج شود. این امر با استفاده از بلوکهای In & Out Connection و تابع MATLAB linmode صورت میگیرد. ابتدا یک بلوک step و بلوک Scope را به ترتیب با بلوکهایConnection In و Connection Out جایگزین مینماییم.
فایل خود را به عنوان «motormod.mdl» ذخیره میکنیم (save as را از file menu انتخاب میکنیم و فایل را save میکنیم).
MATLAB مدل خطی فایل ذخیره شده را استخراج خواهد کرد. در prompt MATLAB دستورات زیر را وارد میکنیم.
[A,B,C,D] = linmod (‘motormod‘)
[num,den] = ss2tf(A,B,C,D)
خروجیهای زیر را میبینیم. (Transfer function & space state)
A =
-۱۰٫۰۰۰ ۱٫۰۰۰۰
-۰٫۰۲۰۰ -۲٫۰۰۰۰
B = ۰
۲
C = ۱ ۰
D =
۰
num =
۰ ۰٫۰۰۰۰ ۲٫۰۰۰۰
den =
۱٫۰۰۰۰ ۱۲٫۰۰۰۰ ۲۰٫۰۲۰۰
برای بررسی درستی مقادیر داده شده، ما پاسخ حلقه باز تابع تبدیل استخراج شده را در MATLAB میبینیم.
Step (num,den);
plotزیر را که با خروجی Scope یکسان است، میبینیم.
۴-۲ روش طراحی PID برای کنترل سرعت موتور dc :
همان طور که میدانیم معادلات دینامیکی و تابع تبدیل حلقه باز یک موتور dc به صورت زیر هستند:
S(Js+b)q(s) = kI(s)
(Ls+R) I(s) = V-ksq(s)
و شماتیک سیستم به صورت زیر است:
با ورودی پله شرایط طراحی به صورت زیر است:
- setting time کمتر از ۲ ثانیه
- over shoot کمتر از ۵%
- خطای حالت ماندگار (steady – state error) کمتر از ۱%
حالا کنترل کننده PID را طراحی میکنیم. ابتدا یک m-file جدید ایجاد میکنیم و دستورات زیر را تایپ میکنیم:
J = 0.01;
b = 0.1;
k = 0.01;
R = 1;
L = 0.5;
num = k;
den = [(J*L) ((J*R)+(L*b)) ((b*R)+k^2)];
motor = tf [num,den];
همان طور که میدانیم یک کنترل کننده PID دارای تابع تبدیل به صورت زیر است :
- Proportional Control :
ابتدا کنترلکننده تناسبی با gain=100 استفاده میکنیم. برای تعیین تابع تبدیل حلقه بسته ما دستور feed back را استفاده میکنیم. کد زیر را در انتهای m-file خود اضافه میکنیم.
Kp=100;
Contr=kp;
sys_cl=feedback (contr*motor,1);
حالا پاسخ بله را مشاهده میکنیم دستورات زیر را به انتهای m-file اضافه میکنیم. و پنجره دستورات را run میکنیم.
t=0:0.01:5;
step(sys_cl,t)
title(‘step response with Proportion Control‘)
plot زیر را مشاهده میکنیم.
۲-۴-۲ PID Control :
همان طور که در Plot بالا میبینیم over shoot و Steady state خیلی بزرگ هستند.
اضافه کردن یک ترم انتگرالگیر خطای حالت ماندگار را حذف خواهد کرد و یک ترم مشتقگیر yovershoot کم خواهد کرد. یک کنترل کننده PID با ki و kd کوچک را امتحان میکنیم. m-file جدیدی به صورت زیر ایجاد میکنیم:
J = 0.01;
b = 0.1;
k = 0.01;
R = 1;
L = 0.5;
num = k;
den = [(J*L) ((J*R)+(L*b)) ((b*R)+k^2)];
motor = tf (num,den);
kp = 100;
ki = 1;
kd = 1;
contr = tf([kd kp ki],[1 ۰]);
sys_Cl = feedback(Contr*motor,1);
step(sys_Cl)
title(‘PID Control with small ki and kd‘)
شکل زیر نتیجه کار را نشان میدهد.
۳-۴-۲ تنظیم مقادیر gain ها:
همان طور که در شکل بالا مِیبینیم setting time بسیار بزرگ است. بنابراین ki را به منظور کاهش setting time افزایش میدهیم. در m-file مربوطه مقدار ki را به ۲۰۰ نغییر میدهیم. شکل زیر نتیجه تغییر ki میباشد.
همان طور که ملاحظه میکنیم، پاسخ بسیار سریعتر از گذشته میباشد، اما ki بزرگ باعث میشود over shoot نیز زیاد شود. بنابراین kd را به منظور کاهش over shoot افزایش میدهیم. در m-file مربوطه kd را به ۱۰ تغییر میدهیم. نتیجه حاصل به صورت زیر میباشد.
بنابراین کنترلکنندهای به صورت زیر داریم.
kp = 100;
ki = 200;
kd = 10;
۵-۲ متد طراحی مکان هندسی ریشهها برای کنترل سرعت موتور dc :
همان طور که در بخش قبلی گفتیم تابع تبدیل موتور dc به صورت زیر است:
و شماتیک سیستم به صورت زیر میباشد.
حالا میخواهیم یک کنترلر با استفاده از متد مکان ریشهها طراحی کنیم.
یک m-file ایجاد میکنیم و دستورات زیر را در آن تایپ میکنیم:
J = 0.01;
b = 0.1;
k = 0.01;
R = 1;
L = 0.5;
num = k;
den = [(J*L) ((J*R)+(L*b)) ((b*R)+k^2)];
motor = tf (num,den);
۱-۵-۲ کشیدن مکان هندسی حلقه باز :
ایده اصلی طراحی مکان هندسی ریشهها پیدا کردن پاسخ حلقه بسته از روی نمودار حلقه باز میباشد. سپس با استفاده از اضافه کردن صفرها و قطبها به plant اصلی، پاسخ حلقه بسته میتواند اصلاح شود. ابتدا مکان ریشه برای Plant را میبینیم. دستورات زیر را به انتهای m-file خود اضافه میکنیم.
rlocus (motor)
sgirid (0.8,0)
title(‘Root Locus Without a Controller‘)
در دستور sgirid دو عبارت وجوددارند که به ترتیب ترمهای نسبت میرایی (zeta) (0.8 مربوط به overshoot=%5 میباشد) و فرکانس طبیعی (wn) (صفر مربوط به میزان rise time) میباشند. m-file بالا را در Command Window اجرا میکنیم. نمودار مکان ریشهها به صورت زیر میباشد:
۲-۵-۲ پیدا کردن gain با استفاده از دستور rlocfind :
همان طور که میدانیم، ما میخواهیم Setting time و Over shoot تا حد امکان کوچک باشند. میرایی بزرگ مربوط به نقاطی از مکان هندسی ریشهها که نزدیک محور حقیقی هستند، میباشد. و پاسخ سریع مربوط به نقاطی از مکان هندسی ریشهها که دور از محور موهومی و سمت چپ آن هستند، میباشد. برای پیدا کردن gain مربوط به یک نقطه روی مکان هندسی ریشهها، ما از دستورrlocfind استفاده میکنیم. ما میتوانیم gain و نمودار پاسخ پله را با استفاده از این gain را همزمان ببینیم. برای انجام این کار، دستورات زیر را در انتهای m-file خود ایجاد کرده و دوباره آن را run میکنیم.
[k,poles] = rlocfind (motor)
sys_cl = feedback(k*motor,1);
t=0:0.01:3;
Step(sys_Cl,t)
title(‘step response with gain‘)
به نمودار مراجعه میکنیم (مکان هندسی ریشهها) و یک نقطه روی مکان هندسی ریشهها در نیمه بین محور حقیقی و میرایی موردنظر برای مثال (-۶+۲٫۵i) انتخاب میکنیم. MATLAB خروجی مشابه زیر را نشان میدهد.
Selected point =
-۵٫۹۵۹۶+۲٫۰۵۱۳i
k =
۱۰٫۰۹۳۴
Poles =
-۶٫۰۰۰۰+۲٫۰۵۱۱i
-۶٫۰۰۰۰-۲٫۰۵۱۱i
ما همچنین نمودار زیر را دریافت میکنیم.
همان طور که میبینیم overshoot وجود ندارد .و setting time تقریباً یک ثانیه است که مقادیر ارضا کنندهای هستند. تنها مشکل که در نمودار میتوان یافت خطای حالت ماندگار که حدوداً ۵۰% میباشد.
اگر ما gain را کاهش دهیم خطای حالت ماندگار کاهش مییابد ولی overshoot خیلی بزرگ میشود. بنابراین کنترل کننده lag برای کاهش خطای حالت ماندگار اضافه میکنیم.
۶-۲ اضافه کردن کنترل کننده lag :
همان طور که در نمودار میبینیم، این یک مکان هندسی ریشههای بسیار ساده است. مقادیر میرایی و setting time با کنترل کننده تناسبی به طور مناسب و ارضا کننده تنظیم میشوند. خطای حالت ماندگار تنها مقداری است که با کنترل کننده تناسبی به طور مطلوب تنظیم نمیشود. با اضافه کردن کنترل کننده lag به هر حال ما ممکن است که setting time را افزایش دهیم. ابتدا کنترل کننده lag به صورت زیر را امتحان میکنیم.
m-file به صورت زیر را ایجاد میکنیم:
J = 0.01;
b = 0.1;
k = 0.01;
R = 1;
L = 0.5;
num = k;
den = [(J*L) ((J*R)+(L*b)) ((b*R)+k^2)];
Z0=1;
P0=0.01;
motor = tf (num,den);
contr = tf ([1 Z0],[1 P0]);
rlocus (contr*motor)
sgirid (0.8,0)
title(‘Root Locus With a Lag Controller‘)
مکان هندسی ریشهها (که بسیار شبیه به نمودار اصلی است) به صورت زیر میباشد.
۱-۶-۲ نمودار پاسخ حلقه – بسته :
حالا میخواهیم حلقه را ببندیم و پاسخ بله حلقه بسته را ببینیم. کدهای زیر را در انتهای m-file خود ایجاد میکنیم.
[k,poles] = rlocfind (cont*motpr)
sys_cl = feed back (k*conter*motor,1);
t=0:0.1:3;
Step (sys_cl,t)
(itle (step response with a lagconteroller t
m-file را دوباره run میکنیم. هنگامی که میخواهیم یک نقطه انتخاب میکنیم یکی که نزدیک به مقدار میرایی مورد نیاز است را، انتخاب میکنیم (در این حالت نمایشگر به صورت خط نقطه دار قطری ظاهر میشود). نمودار مربوط به صورت زیر است.
Gain ما باید حدوداً ۲۰ باشد. همانطور که میبینیم در صورت انتخاب هر gain مربوط به نقطهای نزدیک به مقدار میرایی مورد نظر، overshoot حتی نزدیک به ۵% هم نمیشود و این اثر کنترل کننده lag میباشد. (زیرا قطبش خیلی دور است). این موضوع نشان میدهد که ما میتوانیم gain های بالاتری را هم انتخاب کنیم بدون اینکه نگران overshoot باشیم. M-file را دوباره run میکنیم و gain را (بوسیله خط نقطه دار قطری) جا به جا میکنیم. این کار را همچنان ادامه میدهیم تا پاسخ راضی کنندهای به دست آوریم. نتیجه کار انتخاب gain=50 است.
همانطور که میبینیم در شکل بالا، خطای حالت ماندگار کمتر از ۱% است و setting time و overshoot مقادیر مناسبی هستند. همانطور که ملاحظه میکنیم، فرآیند طراحی برای مکان هندسی ریشهها بر مبنای آزمون سعی و خطا استوار است. به همین دلیل بهتر است مکان هندسی ریشهها رسم شود، gain انتخاب شود پاسخها همه در step رسم شود.
اگر ما نتوانیم یک پاسخ مناسب با انتخاب gain های مختلف بدست آوریم ما باید یک کنترل کننده Lag دیگر انتخاب کنیم و یا حتی یک کنترل کننده Lead اضافه کنیم.
۷-۲ : متر طراحی فرکانسی برای کنترل سرعت موتور DC :
یک m-file جدید ایجاد میکنیم و دستورات زیر را type میکنیم.
J=0.01;
b = 0.1;
k = 0.01;
R=1;
L=0.5;
num=k;
den = [(J*L) ((J*R)+(L*b)) ((b*R)+k^2)];
motor = tf (num ,den);
۲-۷-۱ : کشیدن نمودار Bode
ایده اصلی برای طراحی فرکانسی استفاده از نمودار Bode تابع تبدیل حلقه باز برای تخمین پاسخ حلقه بسته است. اضافه کردن یک کنترل کننده به سیستم، نمودار Bode حلقه باز و در نتیجه پاسخ حلقه بسته را تغییر میدهد ابتدا نمودار Bode برای تابع تبدیل حلقه باز را رسم میکنیم.
کدهای زیر را در انتهای m-file خود اضافه میکنیم و سپس آن را run میکنیم.
bode (motor)
نمودار bode به صورت زیر خواهد بود.
۲-۷-۲ : اضافه کردن گین تناسبی
از نمودار bode بالا، میبینیم که هنگامی که ۵ کمتر از است phas margine بزرگتر از حدوداً °۶۰ درجه است. میخواهیم gain را به سیستم اضافه میکنیم. برای بدست آوردن gain در ما هم میتوانیم از نمودار استفاده کنیم (که به نظر میرسد حدوداً بیشتر از dB 40- است) و هم میتوانیم از دستور bode برای بدست آوردن مقدار دقیق استفاده کنیم.
[mag,phase,w]=bode(motor,10)
mag =
۰٫۰۱۳۹
برای داشتن یک gain = 1 (در سیستم حلقه باز) در ما باید یک کنترل کننده با گین یا تقریباً ۷۲ به سیستم اضافه کنیم.
contr = 72;
bode(contr*motor);
و m-file را دوباره اجرا میکنیم. نمودار « Bode» به صورت زیر است.
۳-۷-۲ نمودار پاسخ حلقه – بسته
همان طور که در نمودار بالا میبینیم phase margine همچنان بزرگ است. میخواهیم پاسخ حلقه بسته را ببینیم در جلوی دستورات bode یک علامت «%» اضافه میکنیم و کدهای زیر را در انتهای m-file خود اضافه میکنیم.
sys_cl=feedback(contr*motor,1);
t = 0:0.01,10;
step(sys_cl,t)
نمودار به صورت زیر خواهد بود.
Setting time مناسب است اما over shoot و خطای حالت ماندگار زیاد است. over shoot با کم کردن gain کم میشود. اما خطای حالت ماندگار زیاد میشود. اضافه کردن یک کنترل کننده Lag میتواند مشکل را بر طرف کند.
۴-۷-۲ اضافه کردن یک کنترل کننده lag
ما میتوانیم یک کنترل کننده lag به سیستم اضافه تا خطای حالت ماندگار کم شود. (و همزمان ما سعی در کاهش over shoot با کم کردن gain داریم). Gain را به ۵۰ کاهش میدهیم و یک کنترل کننده lag به صورت که خطای حالت ماندگار را با نسبت کم میکند. (اما ممکن است Setting time را افزایش میدهد) را امتحان میکنیم. m-file را به صورت زیر تغییر میدهیم.
num = k;
den = [(J*L) ((J*R)+(L*b)) ((b*R)+k^2)];
motor = tf (num ,den);
Z0 = 1;
P0 = 0.01;
Contr = 50*tf([1 z0] , [1 p0];
bode (contr*motor)
نمودار به صورت زیر خواهد بود:
Phase margine به نظر خوب میآید. خطای حالت ماندگار حدود یا ۱% به نظر میرسد که مطلوب است.حلقه را میبندیم و پاسخ بله را مشاهده میکنیم. کدهای زیر را به انتهای m-file اضافه کرده و آن را دوباره run میکنیم.
sys_cl – feedback(contr*motor,1);
t = 0:0.01:10;
step(sys_cl,t)
همان طور که میبینیم ما اکنون یک پاسخ بله که شرایط خواسته شده آن مطلوب است، داریم. خطای حالت ماندگار کمتر از ۱% و over shoot کمتر از ۵% و Setting time حدوداً ۲ ثانیه است.
۸-۲ یک کنترلکننده فضای حالت برای موتور dc :
معادلات دینامیکی در فضای حالت به صورت زیر هستند:
q° = [۱ ۰]
با مقادیر طراحی عبارتند از:
- Setting time کمتر از ۲ ثانیه
- Over shoot کمتر از ۵%
- Stedy-state error کمتر از ۱%
یک m-file جدید ایجاد میکنیم و دستورات زیر را در آن تایپ میکنیم.
J = 0.01;
b = 0.1;
k = 0.01;
R = 1;
L = 0.5;
A = [
];
B = [0
];
C = [1 ۰];
D = 0;
sys = ss[A,B,C,D];
۱-۸-۲ طراحی یک کنترلکننده فیدبک حالت کامل :
از آنجایی که هر دو متغیر در مسئله ما به آسانی اندازهگیری میشوند. (با اضافه کردن یک ammeter برای جریان و یک tachometer برای سرعت)، ما میتوانیم یک کنترل کننده فیدبک حالت کامل برای سیستم (بدون اینکه نگران این باشیم که مجبوریم یک observer اضافه کنیم) طراحی کنیم. شماتیک برای سیستم فیدبک حالت کامل به صورت زیر است:
یادآوری میکنیم که چند جملهای مشخصه برای این سیستم حلقه بسته رابااستفاده ازدترمینان ((SI(A-Bk) که s متغیر U پلاس است، بدست میآوریم. از آنجایی که ماتریس A و B*k هر دو ماتریسهای ۲×۲ هستند، بنابراین باید دو قطب برای سیستم موجود باشد. با استفاده از طراحی یک کنترل کننده فیدبک حالت کامل ما میتوانیم این دو قطب را به هر جایی که میخواهیم منتقل کنیم.
ماابتداسعی میکنیم که قطبها را به (-۵+i) و (-۵-i) منتقل کنیم. (توجه کنید این مقادیر مربوط به zeta = 0.8 که over shoot = 1% و sigma = 5 که setting time = 1s را میدهدف هستند). MATLAB ماتریس کنترلکننده k را پیدا خواهیم کرد. کدهای زیر را در انتهای m-file اضافه میکنیم.
P1 = -5+i;
P2 = -5-i;
k=place (A,B,[P1 P2]);
حالا دوباره به شماتیک بالا نگاه میکنیم. ما میبینیم که بعد از اضافه کردن ماتریس k به سیستم، معادلات فضای حالت به صورت زیر میشود:
x˚ = (A-Bk)x+BU
y = CX
ما میتوانیم پاسخ حلقه بسته را به آسانی با استفاده از اضافه کردن خط زیر در انتهای m-file ببینیم:
t = 0:0.01:3;
sys_cl=ss(A-B*k,B,C,D);
step(sys_cl,t)
m-file را run میکنیم. نمودار به صورت زیر است:
۲-۸-۲ اضافه کردن یک ورودی مرجع:
از نمودار بالا متوجه میشویم که خطای فضای حالت بسیار بزرگ است. در مقایسه با سایر روشهای طراحی، که ما خروجی را فیدبک میکردیم و آن را با مرجع مقایسه میکردیم تا خطا را محاسبه کنیم، اینجا ما دو حالت را فیدبک میکنیم. ما نیاز داریم تا خطای ماندگار حالتها ضرب در gain انتخابی k را محاسبه کنیم و این مقدار جدید را به عنوان مرجع برای محاسبه ورودی استفاده میکنیم. این کار را با استفاده از یک gain ثابت Nbar بعد از مرجع یک جا انجام میشود.
ما با استفاده از دستور rscale در MATLAB میتوانیم عامل Nbar را پیدا کنیم. توجه کنید که تابع rscale یک تابع استاندارد MATLAB نیست، ما باید آن را قبل از استفاده از آن کپی کنیم. حالا ما میتوانیم نمودار پاسخ بله را با استفاده از اضافه کردن کدهای زیر در m-file ببینیم.
t = 0:0.01:10;
step(sys*Nbar,t)
title(‘Step Response With k Controller and Nbar’)
این بار، خطای حالت ماندگار کمتر از ۱% و همه پارامترهای طراحی بسیار خوب هستند.
۹-۲ کنترل دیجیتال موتور dc با استفاده از کنترل کننده PID
در این بخش ما کنترل دیجیتال موتور dc را توضیح خواهیم داد. یک مدل موتور dc دیجیتال با استفاده از تبدیل مدل آنالوگ میتواند بدست آید. (به صورتی که توضیح میدهیم). کنترلکننده برای این موتور با استفاده از روش PID به دست میآید.
تابع تبدیل حلقه باز برای سرعت موتور dc به صورت زیر بدست میآید.
که در آن
R = 1Ω
L = 0.5H
kt = ke = k =0.01
J = 0.01
b = 0.1NmS
V = source viltage
Output(q˚) = Rotating speed
برای ورودی بله داریم :
- Setting time کمتر از ۲ ثانیه
- Overshoot کمتر از ۵%
- خطای حالت ماندگار کمتر از ۱%
۱-۹-۲ تبدیل پیوسته به دیجیتال
قدم اول در طراحی سیستمهای کنترل دیجیتال تبدیل تابع تبدیل پیوسته به تابع تبدیل گسسته است. دستور C2d در «MATLAB» برای ما این کار را انجام میدهد. دستور C2d به بخشهای زیر نیاز دارد:
سیستم sampling time (ts زمان نمونهبرداری)
متد تبدیل
در اینجا ما از متد (‘Zoh‘) Zero-order hold استفاده میکنیم.
با توجه به خواستههای طراحی، Ts را مساوی با ۰٫۱۲s در نظر میگیریم که ثابت زمانی یک سیستم با setting time = 2s است. یک m-file جدید ایجاد میکنیم و دستورات زیر را در آن وارد میکنیم.
R = 1;
L = 0.5;
kt = 0.01;
J = 0.01;
b = 0.1;
num = kt ;
den = [(J*L) ((J*R)+(L*b)) ((R*b)+kt^2)];
motor = tf(num,den)
Ts = 0.12;
motor_d = C2d(motor,Ts,‘zoh‘)
m-file را run میکنیم. داریم :
Transfer function;
Sampling time = 0.12
حالا میخواهیم پاسخ حلقه بسته با gain تناسبی یک را ببینیم. دستور step این کار را برای ما انجام خواهد داد. کدهای زیر در انتهای m-file اضافه کرده و آن را run میکنیم.
sys_cl = feedback(motor_d,1)
[y,T] = step (sys_cl,12);
Stairs (T,y);
Xlable(‘time(s)‘)
Ylable(‘Velocity (rad/s)‘)
title(‘stair step response: original‘)
نمودار به صورت زیر خواهد بود:
۲-۹-۲ کنترلکننده PID :
همان طور که میدانیم تابع تبدیل یک کنترلکننده PID زمان پیوسته به صورت زیر است:
راههای مختلفی برای تبدیل s-plant به z-plant وجود دارد. دقیقترین روش Z=eTS میباشد. ما با این روش تابع تبدیل PID را نمیتوانیم بدست آوریم زیرا تابع تبدیل زمان گسسته، صفرها و قطبهای بیشتری خواهد داشت، که تحققپذیر نیستند. در عوض از تابع تبدیل دو خطی همان طور که در زیر نشان داده شده است، استفاده میکنیم.
همچنین دستور C2d در MATLAB به ما در تبدیل کنترلکننده PID زمان پیوسته به کنترلکننده PID گسسته زمان کمک خواهد کرد. (با استفاده از روش «tustin» کمک خواهد کرد). روش «tustin» از تقریب دو خطی برای تبدیل به گسسته زمان استفاده میکند. بر طبق PID برای پیوسته زمان kp=100 ، ki=200 ، kd=10 . ما همچنین gainهای پیوسته زمان را در اینجا استفاده میکنیم. حالا دستورات زیر را به انتهای m-file قبلی اضافه میکنیم.
%Discrete PID Controller with bilinear approximation
kp = 100;
ki = 200;
kd = 10;
PID = tf([kd kp ki] , [1 ۰]);
Contr = C2d(PID,Ts,‘tustin‘);
حالا میخواهیم ببینیم پاسخ حلقه-بسته با جبرانساز PID شرایط طراحی را ارضا میکند؟
کدهای زیر را به انتهای m-file اضافه کرده و آن را run میکنیم.
sys_cl = feedback(contr*motor_d,1);
[x2,T] = step(sys_Cl,12);
Stairs(T,X2)
Xlable(‘Time(seconds)‘)
Y lable (‘Velocity (rad/s)‘)
title(‘stair step response with PID controller‘)
پاسخ به صورت زیر است:
همان طور که در نمودار بالا میبینیم پاسخ حلقه-بسته پایدار نیست. بنابراین باید یک چیز اشتباه در سیستم جبرانسازی وجود داشته باشد. بنابراین نگاهی به مکان هندسی ریشههای سیستم جبرانسازی شده میاندازیم. دستورات زیر را در انتهای m-file اضافه میکنیم و آن را دوباره Run میکنیم.
rlocus (contr*motor_d)
title (‘Root Locus of Compensted System‘)
همان طور که در نمودار مکان هندسی ریشهها میبینیم، مخرج کنترلکننده PID یک قطب در(۱-) در صفحه Z دارد. ما میدانیم که اگر یک قطب سیستم بیرون دایره واحد باشد سیستم ناپایدار است. این سیستم جبرانسازی شده همواره برای هر گین مثبت ناپایدار خواهد بود زیرا یک زوج صفر و قطب در سمت راست ۱- وجود دارد. بنابراین قطب همواره به سمت چپ و بیرون دایره واحد حرکت خواهد کرد. قطب در ۱- از جبرانساز میآید و ما میتوانیم مکان آنرا با تغییر طراحی جبرانساز جابهجا کنیم. ما آن را به گونهای انتخاب میکنیم تا صفر در ۶۲.۰- را cancle کنیم. این کار باعث میشود سیستم حداقل برای بعضی از gain ها پایدار شود. بنابراین ما یک gain مناسب از نمودار مکان هندسی ریشهها برای ارضاء اهداف طراحی با استفاده از دستور rlocfind انتخاب میکنیم. Code زیر را به m-file اضافه میکنیم.
۱]);contr.den=conv([1 -۱],[
rlocus (contr*motor-d)
title(‘Root Locus of Compenstated System‘);
[k,poles] = rlocfind(contr*motor-d)
sys_cl=feedback(k*contr*motor_d,1);
[x3,T]=step(sys_Cl,12);
stairs(T,x3)
Xlable(‘Time(seconds)‘)
Ylable(‘Velocity (rad/s)‘)
title(‘Stair Step Response With PID Controller‘)
توجه میکنیم که خط اول کدهای بالا به ما اجازه تغییر مخرج تابع تبدیل سیستم را به طور مستقیم میدهد، بدون اینکه مجبور به این باشیم که سیستم را دوباره تعریف کنیم. قطبهای حلقه بسته جدید یک قطب در ۶۲۵.۰- به جای ۱- خواهد داشت که تقریباً صفر جبران نشده را حذف خواهد کرد. در پنجره MATLAB اکنون یک دستور که از ما میخواهد نقطهای روی نمودار مکان ریشهها را انتخاب کنیم، وجود دارد. ما باید روی نمودار کلیک کنیم به صورت زیر:
سپس MATLAB، gain مناسب و قطبهای جبرانسازی شده منطبق بر آن را نمایش میدهد و آن پاسخ جبرانسازی شده حلقه بسته را خواهد کشید. به صورت زیر:
همان طور که شکل نشان میدهد setting time کمتر از ۲ ثانیه و درصد overshoot حدود ۳% است. علاوه بر این خطای حالت ماندگار صفر است. gain از مکان هندسه ریشهها ۲۴۲۵.۰ است که منطقی نیز است. بنابراین این پاسخ همه شرایط طراحی را ارضاء میکند.
فصل سوم
در این فصل کنترل درایو موتور dc را با استفاده از بلوکهای Simpower و simUlink انجام میدهیم.
- مقدمه :
در این فصل ابتدا، با استفاده از بلوکهای simUlink درایو موتور dc را مدل خواهیم کرد، سپس با استفاده از کنترلکننده جریان و کنترلکننده سرعت که هر دو از نوع PI هستند به کنترل سرعت موتور dc میپردازیم.
۲-۳ شبیهسازی موتور الکتریکی :
موتور dc که در این بخش استفاده شده است دارای مشخصات زیر است:
سرعت موتور
ثابت اصطکاک ویسکوز
مقدار اینرسی روتور
اندوکتانس مدار آرمیچر
مقاومت مدار آرمیچر
ثابت ولتاژ = ثابت گشتاور
ولتاژ آرمیچر
جریان آرمیچر
گشتاور بار
۱-۲-۳ مدل موتور dc و بار مکانیکی
در اینجا میخواهیم موتور dc تحریک مستقل (با جریان میدان ثابت) را مدل کنیم. برای کار از روباط مربوط به موتور dc تحریک مستقل استفاده میکنیم.
زیر سیستم موتور dc را به صورت زیر ایجاد میکنیم:
- simUlink را باز کرده و یک پنجره مدل جدید باز میکنیم.
- ابتدا ما انتگرالهای شتاب دورانی و آهنگ تغییرات جریان آرمیچر را مدل خواهیم کرد.
یک بلوک انتگرالگیری (از Linear block library) در مدل قرار میدهیم و خطوط را از ترمینالهای ورودی و خروجیاش رسم میکنیم. خط ورودی را «» و خط خروجی را «» نامگذاری میکنیم. یک بلوک انتگرالگیری زیر بلوک قبلی قرار میدهیم و خطوط را از ترمینالهای ورودی و خروجیاش رسم میکنیم. خط ورودی را «» و خط خروجی را «i» مینامیم.
- سپس ما دو قانون Newton و krichoff را مدل میکنیم. این قوانین در سیستم موتور معادلات زیر را میدهند.
شتاب زاویهای برابر با حاصلضرب در جمع دو ترم (یکی با علامت مثبت و دیگری با علامت منفی) است. به طور مشابه جریان مساوی با حاصلضرب در جمع سه ترم (یکی با علامت مثبت و دو تا با علامت منفی) است.
دو بلوک gain (از Linear block library) برای هر کدام از انتگرالها قرار میدهیم.
مقدار یکی از این بلوکها را به تغییر میدهیم و نام آن را به «Inductance» تغییر میدهیم. مقدار بلوک دیگری را به تغییر میدهیم و نام آن را به «inertia» تغییر میدهیم.
دو بلوک SUM (از Linear block library به مدل کپی میکنیم و علامتهای آنها را به صورت «–+» و «-+-» تغییر میدهیم.
- حالا ما گشتاورهایی که در معادلات نیوتن وجود دارند را اضافه میکنیم. ابتدا ما گشتاور میرا را اضافه میکنیم. یک بلوک gain زیر بلوک «inertia» قرار میدهیم.
مقدار Gain را به b=0.01 تغییر میدهیم و آن را «damping» مینامیم.
خروجی انتگرالگیر زاویهای رابه ورودی بلوک damping gain وصل میکنیم.
یک خط از خروجی damping gain به ورودی منفی بلوک «rotational SUM» میکشیم.
حالا میخواهیم گشتاور آرمیچر را اضافه کنیم.
یک بلوک Gain را به ورودی مثبت بلوک «rotational SUM» وصل میکنیم.
مقدار آن را به k=1.274 تغییر میدهیم و آن را «k» مینامیم.
یک خط از انتگرالگیر جریان به بلوک«kt gain» وصل میکنیم.
- اکنون ترمهای ولتاژ که در معادلات kirchoff ظاهر میشوند را اضافه میکنیم. ابتدا ما افت ولتاژ مقاومت هسته را اضافه میکنیم.
یک بلوک gain بالای بلوک Inductance قرار میدهیم.
مقدار آن را به R=0.78 تغییر میدهیم و آن را «Resistance» مینامیم.
خروجی انتگرالگیر جریان و ورودی بلوک «Resistance gain» را به هم وصل میکنیم.
از خروجی «Resistance gain» به ورودی بالایی «SUM block» جریان وصل میکنیم.
مقدار آن را به k=1.274 تغییر میدهیم و آن را «ke» مینامیم.
خروجی انتگرالگیر زاویهای و بلوک «ke gain» را به هم وصل میکنیم.
- همان طور که میدانیم موتور ما دارای دو ورودی یعنی Va (که سومین ترم در معادله kirchoff است) و TL (گشتاور بار) و دو خروجی یعنی Ia (جریان آرمیچر) و W (سرعت موتور) است. بنابراین برای ایجاد زیر سیستم موتور دو بلوک وردی In (از Linear block library) و دو بلوک خروجی Out (از Linear block library) به مدل کپی میکنیم.
یکی از بلوکهای In (ورودی) را Va مینامیم و آن را به وسیله یک خط به ورودی مثبت بلوک SUM جریان وصل میکنیم. بلوک دیگری را TL مینامیم و آن را به ورودی منفی «Rotational SUM» با یک خط وصل میکنیم. حالا نوبت به خروجیها رسیده است. یکی از بلوکهای خروجی (Out) را Ia مینامیم و آن از بعد از بلوک انتگرالگیر جریان قرار میدهیم. از خروجی انتگرالگیر جریان خطی به ورودی بلوک خروجی Ia وصل میکنیم. بلوک خروجی دیگر را W مینامیم و از خروجی انتگرالگیر سرعت به ورودی آن وصل میکنیم.
اکنون میخواهیم مدل ایجاد شده را تبدیل به یک زیر سیستم (Subsystem) کنیم. در پنجره مدل گزینه Edit>select all را انتخاب میکنیم و سپس Edit>Creat Subsystem را انتخاب میکنیم. نام این زیر سیستم را به Motor Subsystem تغییر میدهیم.
اکنون مدل موتور در simUlink ایجاد شده است. قبل از اینکه به بحث کنترل سرعت این موتور dc بپردازیم ابتدا این موتور را به صورت حلقه باز (open loop) امتحان میکنیم.
این موتور دارای سرعت نامی (rad/s)150، ولتاژ نامی آرمیچر Va=220V و گشتاور بار TL=50 است.
ابتدا دو بلوک ثابت (از Commonly Used block) و سه بلوک To workspace (Sink library) و یک بلوک Clock (Source library) به مدل کپی میکنیم. یکی از بلوکهای constaint را Va مینامیم و مقدار آن را به V220 تغییر میدهیم. بلوک دیگر را TL مینامیم و مقدار آن را به ۵۰ تغییر میدهیم. بلوک Va زیر سیستم موتور و بلوک TL را به ورودی TL زیر سیستم موتور وصل میکنیم. یکی از بلوکهای To workspace را به خروجی W زیر سیستم موتور وصل میکنیم. با دوبار کلیک راست کردن روی این بلوک، پنجره مربوط به آن را باز میکنیم. در این پنجره نام بلوک را از To workspace به W تغییر میدهیم و در قسمت Structure گزینه array را انتخاب میکنیم. بلوک To workspace دیگر را به خروجی Ia زیر سیستم موتور وصل میکنیم. با دو بار کلیک راست کردن روی این بلوک، پنجره مربوط به آن را باز میکنیم. در این پنجره نام بلوک را از To workspace به I تغییر میدهیم و در قسمت Structure گزینه array را انتخاب میکنیم.
بلوک Clock را به بلوک To workspace بعدی وصل میکنیم. در پنجره مربوط به بلوک To workspace نام آن را به t و در قسمت Structure گزینه array را انتخاب میکنیم.
اکنون آماده ایم Simulation را run کنیم. Stop time راs5.1 انتخاب میکنیم و سپس Simulation را Start میکنیم. بعد از پایان شبیهسازی، در Work space MATLAB دستور plot(t,w) را تایپ میکنیم نمودار مربوط به سرعت به صورت زیر است:
سپس دستور plot(t,I) را تایپ میکنیم نمودار مربوط به جریان به صورت زیر است:
۳-۳ کنترل سرعت موتور dc
در اینجا، برای کنترل موتور dc از دو حلقه فیدبک استفاده میشود. حلقه اول (کنترلکننده سرعت) برای پایدارسازی جریان آرمیچر استفاده میشود. و حلقه دوم (کنترل کننده جریان) برای پایدارسازی موتور dc استفاده میشود.
خطای جریان آرمیچر (که اختلاف جران مرجع آرمیچر (Ia*) و جریان واقعی آرمیچر (Ia) است) (Ia*-Ia) سیگنال ورودی کنترلکننده جریان است. خروجی کنترلکننده جریان زاویه α مناسب برای pulse generator را فراهم میکند و خروجی pulse generator فرمان آتش کردن گیت یکسوساز تریستوری را میدهد. در حقیقت بوسیله کنترلکننده جریان زاویه آتش تریستورها و در نتیجه ولتاژ آرمیچر را کنترل میکنیم.
کنترلکننده سرعت و کنترل کننده جریان، یک سیستم کنترل سری را تشکیل میدهند. اختلاف سرعت مرجع و سرعت واقعی (w*-w) خطای سرعت را تولید میکند که به عنوان سیگنال ورودی کنترلکننده سرعت عمل میکند. خروجی کنترلکننده سرعت، سیگنال مرجع برای کنترلکننده جریان (Ia) است. توجه به این نکته ضروری است که در خروجی هر دو کنترلکننده یک محدودکننده قرار گرفته است. محدودکننده که در خروجی کنترلکننده سرعت قرار میگیرد جریان آرمیچر را محدود میکند تا از مقدار مجاز بالاتر نرود. محدودکننده موجود درخروجی کنترلکننده جریان، زاویه α را در بین مقادیر ۰ تا ۱۸۰ درجه محدود میکند.
۱-۳-۳ مدلسازی کنترلکننده سرعت:
کنترلکننده سرعت، یک PI کنترلر است. بنابراین از دو ترم تناسبی و انتگرالی تشکیل شده است. برای ایجاد زیر سیستم کنترلکننده سرعت مراحل زیر را انجام میدهیم:
- ابتدا دو بلوک Gain، یک بلوک انتگرالگیر (از Linear block library) به پنجره مدل خود کپی میکنیم.
- نام یکی از بلوکهای گین را به kp۱ تغییر میدهیم. همچنین مقدار آن را نیز به kp1 تغییر میدهد. بلوک گین دیگر را ki1 مینامیم و مقدار آن را نیز به ki1 تغییر میدهیم.
- خروجی بلوک گین ki1 را به ورودی بلوک انتگرالگیر وصل میکنیم.
- دو بلوک sum (از Linear block library) و یک بلوک محدودکننده (از Discontinuties ) به پنجره مدل کپی میکنیم.
- علامت یکی از بلوکهای SUM را به صورت «++» تغییر میدهیم و خروجی بلوک گین kp1 و خورجی بلوک انتگرالگیر را به ورودیهای آن وصل میکنیم. خروجی بلوک SUM را نیز به ورودی بلوک محدودکننده وصل میکنیم. پنجره مربوط به محدودکننده را با دوبار کلیک راست کردن روی آن باز میکنیم. در این پنجره حد پایین Lower limit راصفرو حد بالا Upper limit را )از آنجایی که جریان آرمیچر A40 است( ۴۰ وارد میکنیم.
- قبل از اینکه زیر سیستم را کامل کنیم به این نکته توجه میکنیم که هم در کنترلکننده سرعت و هم در کنترلکننده جریان برای از بین بردن هارمونیکهای ناخواسته سرعت و جریان موجود در سیگنالهای اندازهگیری شده از فیلترهای مرتبه اول استفاده میکنیم. این هارمونیکهای ناخواسته بوسیله ولتاژ خروجی یکسو شده یکسوساز سه فاز بوجود میآیند. فرکانس ریپل اصلی، ایجاد شده بوسیله یکسو کننده سه فاز، ۶ برابر فرکانس منبع تغذیه است. (ششمین هارمونیک). چون فرکانس منبع ما Hz50 است بنابراین اولین فرکانس Hz300 میباشد. بنابراین فرکانس قطع فیلتر مرتبه اول که استفاده میشود باید خیلی پایینتر از این فرکانس باشد تا harmonic rejection خوب و منطقی داشته باشیم. (البته فرکانس قطع خیلی کم میتواند سیستم را ناپایدار کند).
برای ایجاد فیلتر مرتبه اول یک بلوک Transfer Fcn (از Linear block library) به پنجره مدل کپی میکنیم و نام آن را به Filter تغییر میدهیم. پنجره مربوط به این بلوک را با دوبار کلیک کردن روی آن باز میکنیم در قسمت مربوط به Num عدد [۱]، و در قسمت مربوط به den اعداد [۱۱e-5 ] را وارد میکنیم سپس Ok میکنیم.
- دو بلوک ورودی In (از Linear block library) و یک بلوک Out خروجی (از Linear block library) به پنجره مدل کپی میکنیم.
نام یکی از بلوکهای In را به w* تغییر میدهیم و آن را به ورودی مثبت بلوک SUM دومی وصل میکنیم. نام بلوک دیگر In را به w تغییر میدهیم و آن را به ورودی بلوک Filter وصل میکنیم. خروجی بلوک Filter را به ورودی متن بلوک SUM دومی وصل میکنیم. از خروجی این بلوک SUM به ورودی بلوک گین kp1 و بلوک گین ki1 وصل میکنیم.
خروجی بلوک محدود کننده را به ورودی بلوک Out که نام آن را به Ia* تغییر دادهایم، وصل میکنیم اکنون آمادهایم که زیر سیستم را ایجاد کنیم از منوی Edit گزینه Select all را انتخاب میکنیم. سپس از همین منو گزینه Creat Subsystem را انتخاب میکنیم. زیر سیستم مربوطه ایجاد میشود. نام این زیر سیستم را به speed controller تغییر میدهیم.
۲-۳-۳ مدلسازی کنترلکننده جریان
کنترل کننده جریان نیز مانند کنترلکننده سرعت، یک PI کنترلر است. برای ایجاد این کنترلکننده مراحل زیر را طی میکنیم:
- دو بلوک Gain (از Linear block library) و یک بلوک انتگرالگیر از (از Linear block library) به پنجره مدل کپی میکنیم.
- نام یکی از بلوکهای گین را به kp2 تغییر میدهیم. همچنین مقدار آن را نیز به kp2 تغییر میدهیم. بلوک گین دیگر را ki2 مینامیم و مقدار آن را نیز به ki2 تغییر میدهیم.
- خروجی بلوک گین ki2 را به ورودی بلوک انتگرالگیر وصل میکنیم.
- سه بلوک SUM (از Linear block library) و سه بلوک محدود کننده (از Discontinuties) به پنجره مدل کپی میکنیم.
- علامت یکی از بلوکهای SUM را به صورت «++» تغییر میدهیم. خروجی بلوک گین kp2 و خروجی بلوک انتگرالگیر را به ورودیهای آن وصل میکنیم. خروجی بلوک SUM را نیز به ورودی یک بلوک محدودکننده وصل میکنیم. از آنجایی که میخواهیم از خروجی محدودکننده acoss بگیریم (coss وارون) و این تابع فقط ورودی بین ۱- و ۱+ را میپذیرد، در بلوک محدود کننده حد پایین را ۱- و حد بالا را ۱+ تنظیم میکنیم.
- یک بلوک Fcn MATLAB (از User defined function) به پنجره مدل کپی میکنیم و با دو بار کلیک راست کردن روی آن، پنجره مربوط به این بلوک را باز میکنیم. تابع acoss را برای این بلوک انتخاب میکنیم.
خروجی بلوک محدود کننده را به ورودی این بلوک وصل میکنیم.
خروجی تابع acoss به رادیان محاسبه میشود ولی puls generator ورودی را به درجه میپذیرد پس لازم است خروجی رادیان به درجه تبدیل شود. پس از یک بلوک ثابت Constaint برای این تبدیل استفاده میکنیم.
- یک بلوک Constaint (از Linear block library) به پنجره مدل کپی میکنیم. مقدار آن را به تغییر میدهیم . خروجی بلوک acoss را به ورودی بلوک ثابت وصل میکنیم.
- یکی از بلوکهای Sum را به صورت «++» تغییر علامت میدهیم. خروجی بلوک ثابت را به یکی از ورودیهای این Sum وصل میکنیم.
- همان طور که در بخش قبل گفته شد، باید در این کنترلکننده از فیلتر استفاده کنیم. بنابراین یک بلوک Transfer Fcn (از Linear block library) به پنجره مدل کپی میکنیم. در پنجره این بلوک در قسمت Num عدد [۱]، و در قسمت den اعداد [۱۱e-5 ] را وارد میکنیم. نام این بلوک را به Filter تغییر میدهیم.
- دو بلوک ورودی In و یک بلوک خروجی Out (از Linear block library) به پنجره مدل کپی میکنیم.
یکی از بلوکهای ورودی را به نام Ia* تغییر میدهیم و بلوک ورودی دیگر را به نام Ia تغییر میدهیم. یک بلوک SUM را به صورت «- +» تغییر علامت میدهیم. خروجی بلوک ورودی Ia* را به ورودی مثبت بلوک SUM وصل میکنیم. خروجی بلوک ورودی Ia را به ورودی بلوک Filter وصل میکنیم. خروجی بلوک فیلتر را به ورودی منفی بلوک SUM وصل میکنیم.
- از خروجی بلوک ورودی Ia* ، خط دیگری به ورودی یکی دیگر از بلوکهای Saturation (محدودکننده) وصل میکنیم. حد پایین این محدودکننده را در ۱- و حد بالای آن را در ۱+ تنظیم میکنیم (چون میخواهیم از خروجی آن acoss بگیریم).
- یک بلوک Fcn MATLAB (از User defined function) به پنجره مدل کپی میکنیم و در پنجره آن acoss را انتخاب میکنیم. خروجی بلوک محدودکننده را به ورودی بلوک acoss وصل میکنیم.
یک بلوک ثابت از (Commonly Used Block) به پنجره مدل کپی میکنیم و مقدار آن را به ۳/۵۷ تغییر میدهیم. خروجی بلوک acoss را به ورودی بلوک ثابت وصل میکنیم و خروجی بلوک ثابت را به ورودی بلوک SUM آخری وصل میکنیم.
اکنون آماده ایجاد زیر سیستم کنترلکننده جریان هستیم. از گزینه Edit>select all استفاده میکنیم سپس Edit>creat subsystem را استفاده میکنیم. زیر سیستم مربوطه ایجاد میشود. نام این زیر سیستم را به Current Controller تغییر میدهیم.
۴-۳ اضافه کردن منبع سه فاز:
در این طرح کنترلی از یک یکسوساز سه فاز و همچنین pulse generator استفاده میشود، که هر دوی آنها از منبع سه فاز تغذیه میشوند. پس نیاز داریم که یک منبع سه فاز به plant خود اضافه کنیم.
زیر سیستم منبع سه فاز را به صورت زیر ایجاد میکنیم:
- در ابتدا سه منبع ولتاژ تک فاز (از Electrical Source library) به پنجره مدل کپی میکنیم. یکی از این سه منبع را Va مینامیم و در پنجره مربوط به این بلوک اصلاحات زیر را انجام میدهیم:
- peak amplitude(V)=220*sqrt(2)
- phase(deg)=0
- frequency=50Hz
منبع ولتاژ دیگری را Vb مینامیم و در پنجره مربوط به این بلوک اصلاحات زیر را انجام میدهیم:
- peak amplitude=220*sqrt(2)
- phase(deg)=-120
- frequency=50Hz
منبع ولتاژ آخری را Vc مینامیم و در پنجره مربوط به این بلوک اصلاحات زیر را انجام میدهیم:
- peak amplitude=220*sqrt(2)
- phase(deg)=120
- frequency=50Hz
- سه بلو خروجی (Out) (از Linear block library) به مدل کپی میکنیم. آنها را Out1,Out2,Out3 مینامیم. Out1 را به پایانه مثبت Va، Out2 را به پایانه مثبت Vb، Out3 را به پایانه مثبت Vc وصل میکنیم.
اکنون آماده ایجاد زیر سیستم منبع سه فاز هستیم. از منوی Edit گزینه select all را انتخاب میکنیم. سپس از منوی Edit گزینه creat subsystem را انتخاب میکنیم. زیر سیستم مربوطه ایجاد میشود. نام این زیر سیستم را به ۳-phase source تغییر میدهیم.
۵-۳ اضافه کردن پالس ژنراتور و یکسوساز:
همان طور که گفتیم خروجی کنترلکننده جریان به پالس ژنراتور (pulse generator) وارد میشود. این بلوک را از Extras/Control box library به پنجره مدل اضافه میکنیم. این بلوک دارای ۵ ورودی به نامهای Alpha (بر حسب درجه)، AB، BC، CA (تغذیه پالس ژنراتور) و Block است.
بلوک یکسوساز (Universal Bridge) را از Power Electronical library به پنجره مدل اضافه میکنیم. این بلوک دارای ۴ ورودی به نامهای g (که گیت تریستورها از این طریق تریگ میشوند)، A و b و C (تغذیه یکسوساز) است.
۶-۳ مدلسازی کل سیستم
اکنون که کنترلکننده سرعت، کنترل کننده جریان، زیر سیستم موتور، زیر سیستم منبع سه فاز را مدلسازی کردیم، و یکسو ساز و پالس ژنراتور را به پنجره مدل اضافه کردیم، کل سیستم را میتوانیم مدلسازی کنیم.
ابتدا زیر سیستم کنترلکننده سرعت را قرار میدهیم. خروجی زیرسیستم کنترلکننده سرعت (Ia*) را به ورودی Ia* زیرسیستم کنترلکننده جریان وصل میکنیم. خروجی زیرسیستم کنترلکننده جریان را به ورودی Alpha مربوط به پالس ژنراتور وصل میکنیم. خروجی پالس ژنراتور را به ورودی g از یکسوساز (Universal Bridge) وصل میکنیم.
از آنجا که خروجی یکسوساز ولتاژ آرمیچر است، باید خروجی یکسوساز را به ورودی Va ، زیرسیستم موتور وصل کنیم، از آنجا که پایانههای خروجی یکسو ساز به صورت دو مستطیل است و نه به صورت مثلث باید برای اتصال خروجی یکسوساز به ورودی Va، زیرسیستم موتور از یک بلوک Voltage measurment استفاده میکنیم. پس یک بلوک Voltage measurment از simpower/measurment به مدل کپی میکنیم. خروجی یکسوساز را به ورودی این بلوک وصل میکنیم، خروجی بلوک Voltage measurment را به ورودی Va از زیر سیستم موتور وصل میکنیم.
اکنون باید تغذیه پالس ژنراتور باید از سه بلوک Voltage measurment استفاده میکنیم. سه بلوک Voltage measurment از simpower/measurment library به پنجره مدل کپی میکنیم. خروجی Out1 ، Out2 از زیرسیستم منبع سه فاز را به ترتیب به ورودیهای مثبت و منفی یک بلوک Voltage measurment وصل میکنیم و خروجی این بلوک را به ورودی AB پالس ژنراتور وصل میکنیم. خروجی Out1,Out3 از زیر سیستم منبع سه فاز را به ترتیب به ورودیهای مثبت و منفی یک بلوک Voltage measurment دیگر وصل میکنیم و خروجی ابن بلوک را به ورودی CA پالس ژنراتور وصل میکنیم. برای ورودی Block پالس ژنراتور، یک بلوک ثابت (Constant) (از Commonly used block) به پنجره مدل کپی میکنیم، مقدار این بلوک را به صفر تغییر میدهیم. خروجی بلوک را به ورودی Block، پالس ژنراتور وصل میکنیم.
خروجی w، زیرسیستم موتور را به ورودی w، کنترلکننده سرعت وصل میکنیم. همچنین خروجیI، زیرسیستم موتور را به ورودی I، کنترلکننده جریان وصل میکنیم.
برای ورودی TL از زیرسیستم موتور، نیاز به یک مقدار ثابت و یک مقدار بله داریم. بنابراین یک بلوک ثابت (Constant) (از Commonly used block) و یک بلوک Step (از Source switch) و یک کلید دستی (Manual Switch) به پنجره مدل کپی میکنیم. مقدار بلوک ثابت را به ۵۰ تغییر میدهیم. مقدار بله را به صورت Initial value=50 و Final value=60 تغییر میدهیم. Manual Switch را طوری قرار میدهیم که بتوانیم بین Constant و Step، عمل Switch را انجام دهیم.
برای ورودی w* از زیر سیستم کنترلکننده سرعت، نیز نیاز به یک مقدار ثابت و همچنین یک مقدار بله داریم بنابراین طبق بخش بالا، یک بلوک ثابت، یک بلوک Step و یک Manual Switch به پنجره مدل کپی میکنیم. مقدار بلوک ثابت مقدار مطلوب سرعت است و مقدار اولیه و نهایی بله نیز مقدار Step است که ما میخواهیم در سرعت قرار دهیم.
۷-۳ تنظیم پارامترهای کنترلکننده سرعت و کنترلکننده جریان با استفاده از NCD :
برای تنظیم پارامترهای کنترلکنندهها، از بلوک NCD استفاده میکنیم. طبق نکانی که در فصل «مقدمهای بر Simulink Response Optimization » گفتیم. اولین قدم در این راه این است که بلوک NCD از «Simulink Response Optimization» را به پنجره مدل کپی میکنیم.
سپس پارامترهای مدل را در «Work space MATLAB» وارد میکنیم. مقادیر اولیه برای kp1 ، ki1 ، kp2 ، ki2 (که از آزمون سعی و خطا به دست آمدهاند عبارتند از kp1=1.6 , ki1=16 , kp2=0.5 , ki2=5). بنابراین این مقادیر را در «Work space MATLAB» وارد میکنیم.
روی NCD Block دوبار کلیک میکنیم. تا پنجره مربوط به آن باز شود. در انتهای این پنجره Check box Enforce Signal bounds را انتخاب میکنیم.
از منوی Optimization گزینه Tuned parameter را انتخاب میکنیم. هنگامی که پنجره مربوط به parameter Tuned باز شد، روی گزینه Add که در سمت پایین و چپ این پنجره قرار دارد کلیک میکنیم. با این کار لیستی از پارامترهایی که ما در MATLAB workspace وارد کردهایم (یعنی kp1 ، ki1 ، kp2 ، ki2 ) ظاهر میشود. در این لیست ما، ki1 ، ki2، kp1 ، kp2 را انتخاب میکنیم.
(به عنوان پارامترهایی که قرار است تنظیم شوند) و سپس ok میکنیم. با این کار این پارامترها جز لیست Tuned parameter که در سمت چپ پنجره مربوطه قرار دارد، قرار میگیرند. مشخصات این پارامترها را که در سمت راست این پنجره Tuned parameter قرار دارند، به صورت زیر اصلاح میکنیم.
در مورد پارامتر kp1 ، مقدار ماکزیمم آن را به ۷.۱ و مقدار مینیمم آن را به ۵.۱ تغییر میدهیم.
در مورد پارامترkp2 ، مقدار ماکزیمم آن را به ۶.۰ و مقدار مینیمم آن را به ۴.۰ تغییر میدهیم.
در مورد پارامتر ki1 ، مقدار ماکزیمم آن را به ۱.۱۶ و مقدار مینیمم آن را به ۹.۱۵ تغییر میدهیم.
در مورد پارامتر ki2 ، مقدار ماکزیمم آن را به ۱.۵ و مقدار مینیمم آن را به ۹.۴ تغییر میدهیم.
در پایان در پنجره Tuned parameter روی ok کلیک میکنیم تا تنظیمات انجام شده، save گردد.
حالا به سراغ تنظیم قیود setting time، over shoot، rise time میرویم..
از منوی Goals گزینه Desired Response را انتخاب میکنیم. در پنجره باز شده ما گزینه specify step response characteries را انتخاب میکنیم. با این کار پنجره مربوط به تنظیمات پاسخ پله ظاهر میشود. در این پنجره اصلاحات زیر را انجام میدهیم.
- در قسمت مربوط به ورودی پله مقدار اولیه را به صفر، مقدار نهایی را به ۱۵۰ و step time را به صفر تغییر میدهیم.
- rise time را به ۱.۰ تغییر میدهیم.
- setting time را به ۴.۰ تغییر میدهیم.
- over shoot را به ۱۰% تغییر میدهیم.
- Setting% را به ۰۰۰۵.۰ تغییر میدهیم.
حالا که پارامترهای تنظیمپذیر را تعیین کردیم و پاسخ بله مطلوب را تعیین کردیم، میتوانیم Optimization را شروع کنیم. قبل از شروع بهینهسازی دقت میکنیم که بلوک موجود در مدل simUlink نیز باید دارای step time =0 باشد.
با انتخاب optimization>simulation optimization، پنجره مربوط به تنظیمات شبیهسازی را انتخاب میکنیم و در آن stop time را به ۱٫۵s تغییر میدهیم از آنجائیکه مدل ما شامل بخشهای غیرخطی میشود در بخش slove باید ode15 یا ode45 را انتخاب کنیم. سپس روی ok کلیک میکنیم. optimization>start را انتخاب میکنیم تا بهینهسازی run شود. نمودارهای رسم شده در پنجره signal constraint به صورت زیر است.
همچنین پنجره progress window نتیجه محاسبات برای ki1 ، ki2، kp1 ، kp2 را به صورت زیر نشان میدهد.
kp1=1.6,ki1=16,kp2=0.5,ki2=5
در پایان برای اطمینان از نتیجه حاصل شده Simulation را با مقادیر بدست آمده برای kp1 ، kp2، ki1 ، ki2برای چندین سرعت مختلف و گشتاور run میکنیم. که نتایج به صورت زیر است.
فصل چهارم
در این فصل تلاش میکنیم با مدلسازی بخشهای مختلف (مثل موتور، یکسوساز و …) به طراحی کنترلکنندهها بپردازیم.
- مقدمه:
طرح کنترلی ما در این فصل بر اساس مدل ریاضی plant استوار است. plant واقعی همیشه غیر خطی است. پارامترهای الکتریکی موتور dc که غیر خطی هستند، باعث اشباع و گرم شدن موتور میشوند. پارامترهای بار مکانیکی و اینرسیها (نظیر J وb) نیز ممکن است ثابت نباشند و بین دو مقدار ماکزیمم و مینیمم تغییر کنند.
۲-۴ شبیهسازی مدل درایو الکتریکی
در این فصل از یک مدل خطی برای درایو dc استفاده خواهد شد. مدل درایو الکتریکی شامل بخشهای زیر است:
موتور الکتریکی با بار (سیستم مکانیکی) و یکسوساز تریستوری (thyristor converter) که موتور dc را تغذیه میکند. یک مدل درایو dc با سیستم کنترل کلاسیک که با استفاده از بلوکهای simUlink ساخته شده است، در شکل زیر نشان داده شده است.
شکل (۱)
موتور dc که در این بخش استفاده شده است دارای مشخصات زیر است:
w = 150(rad/s) سرعت موتور
B = 0.01N.m/s ثابت اصطکاک ویسکوز
J = 0.05kgm2/s2 مقدار اینرسی روتور
La = 0.016H اندوکتانس مدار آرمیچر
Ra = 0.78Ω مقاومت مدار آرمیچر
k = kt = kv = 1.274 ثابت ولتاژ = ثابت گشتاور
Va = 220V ولتاژ آرمیچر
Ia =40A جریان آرمیچر
TL = گشتاور بار
۱-۲-۴ مدل موتور dc و بار مکانیکی
در این جا میخواهیم موتور dc تحریک مستقل (با جریان میدان ثابت) را مدل کنیم. برای این کار از روابط مربوط به موتور dc تحریک مستقل استفاده میکنیم.
زیر سیستم موتور dc را به صورت زیر ایجاد میکنیم:
- simUlink را باز کرده و یک پنجره مدل جدید باز میکنیم.
- ابتدا ما انتگرالهای شتاب دورانی و آهنگ تغییرات جریان آرمیچر را مدل خواهیم کرد.
یک بلوک انتگرالگیر (از Linear block lobrary) در مدل قرار میدهیم و خطوط را از ترمینالهای ورودی و خروجیاش رسیم میکنیم. خط ورودی را خط ورودی را «» و خط خروجی را «» نامگذاری میکنیم. یک بلوک انتگرالگیر دیگر زیر بلوک قبلی قرار میدهیم و خطوط را از ترمینالهای ورودی و خروجیاش رسم میکنیم. خط ورودی را «» و خط خروجی را «i» مینامیم.
- سپس ما دو قانون Newton و krichoff را مدل میکنیم. این قوانین در سیستم موتور معادلات زیر را میدهند.
شتاب زاویهای برابر با حاصلضرب در جمع دو ترم (یکی با علامت مثبت و دیگری با علامت منفی) است. به طور مشابه جریان مساوی با حاصلضرب در جمع سه ترم (یکی با علامت مثبت و دو تا با علامت منفی) است.
دو بلوک gain (از Linear block library) برای هر کدام از انتگرالها قرار میدهیم.
مقدار یکی از این بلوکها را به تغییر میدهیم و نام آن را به «Inductance» تغییر میدهیم. مقدار بلوک دیگری را به تغییر میدهیم و نام آن را به «inertia» تغییر میدهیم.
دو بلوک SUM (از Linear block library به مدل کپی میکنیم و علامتهای آنها را به صورت «- – +» و «- + -» تغییر میدهیم.
- حالا ما گشتاورهایی که در معادلات نیوتن وجود دارند را اضافه میکنیم. ابتدا ما گشتاور میرا را اضافه میکنیم. یک بلوک gain زیر بلوک «inertia» قرار میدهیم.
مقدار Gain را به b=0.01 تغییر میدهیم و آن را «damping» مینامیم.
خروجی انتگرالگیر زاویهای رابه ورودی بلوک damping gain وصل میکنیم.
یک خط از خروجی damping gain به ورودی منفی بلوک «rotational SUM» میکشیم.
حالا ما گشتاور آرمیچر را اضافه کنیم.
یک بلوک Gain را به ورودی مثبت بلوک «rotational SUM» وصل میکنیم.
مقدار آن را به k=1.274 تغییر میدهیم و آن را «kt» مینامیم.
یک خط از انتگرالگیر جریان به بلوک«kt gain» وصل میکنیم.
- اکنون ترمهای ولتاژ که در معادلات kirchoff ظاهر میشوند را اضافه میکنیم. ابتدا ما افت ولتاژ مقاومت هسته را اضافه میکنیم.
یک بلوک gain بالای بلوک Inductance block قرار میدهیم.
مقدار آن را به R=0.78 تغییر میدهیم و آن را «Resistance» مینامیم.
خروجی انتگرالگیر جریان و ورودی بلوک «Resistance gain» را به هم وصل میکنیم.
از خروجی «Resistance gain» به ورودی بالایی «SUM block» جریان وصل میکنیم.
مقدار آن را به k=1.274 تغییر میدهیم و آن را «ke» مینامیم.
خروجی انتگرالگیر زاویهای و بلوک «ke gain» را به هم وصل میکنیم.
- همان طور که میدانیم موتور ما دارای دو ورودی یعنی Va (که سومین ترم در معادله kirchoff است) و TL (گشتاور بار) و دو خروجی یعنی Ia (جریان آرمیچر) و W (سرعت موتور) است. بنابراین برای ایجاد زیر سیستم موتور دو بلوک وردی In (از Linear block library) و دو بلوک خروجی Out (از Linear block library) به مدل کپی میکنیم.
یکی از بلوکهای In (ورودی) را Va مینامیم و آن را به وسیله یک خط به ورودی مثبت بلوک SUM جریان وصل میکنیم. بلوک ورودی (In) را TL مینامیم و آن را به ورودی منفی «Rotational SUM» با یک خط وصل میکنیم.
حالا نوبت به خروجیها رسیده است. یکی از بلوکهای خروجی (Out) را Ia مینامیم و آن را بعد از بلوک انتگرالگیر جریان قرار میدهیم. از خروجی انتگرالگیر جریان خطی به ورودی بلوک خروجی Ia وصل میکنیم.
بلوک خروجی دیگر را w مینامیم و از خروجی انتگرالگیر سرعت به ورودی آن وصل میکنیم.
اکنون میخواهیم مدل ایجاد شده را تبدیل به یک زیر سیستم (Subsystem) کنیم. در پنجره مدل گزینه Edit>select all را انتخاب میکنیم و سپس Edit>Creat Subsystem را انتخاب میکنیم. نام این زیر سیستم را به زیرسیستم موتور تغییر میدهیم.
۲-۲-۴ مدل کردن یکسوساز
یکسوساز پل سه فاز اغلب در سیستمهای کنترلی مورداستفاده قرار میگیرد. در کنترل دور موتور dc از یک یکسوساز کنترلشده ۶ پالسه استفاده میشود.
مدل یکسوساز به صورت ساده با یک تابع تبدیل مرتبه اول مطابق فرمول زیر توضیح داده میشود:
که در آن
Va ولتاژ خورجی یکسوساز که در اینجا ولتاژ آرمیچر است.
V ولتاژ ورودی یکسوساز که در اینجا خروجی کنترلکننده جریان است.
Kp گین یکسوساز
Tmip زمان مرده (dead time)
میباشد.
ما مقادیر kp و Tmip را به ترتیب ۱۰۰ و (s)0.02 فرض کردهایم.
همان طور که در بالا اشاره شد، ولتاژ خروجی کنترل کننده جریان (V) برای کنترل زاویه آتش تریستورها در یکسو کننده تمام موج که موتور dc را تغذیه میکند، استفاده میشود.
بنابراین برای مدل کردن یک یکسوساز در simUlink فقط نیاز به یک بلوک تابع تبدیل داریم.
یک بلوک تابع تبدیل یعنی Transfer Fcn (از Linear block library) به پنجره مدل کپی میکنیم و نام آن را به Converter Transfer تغییر میدهیم. روی این بلوک دو بار کلیک راست میکنیم تا پنجره مربوط به آن باز شود. در این پنجره در قسمت مربوط به Num «kp» و در قسمت مربوط بهden [tmip ۱] را وارد میکنیم. سپس روی ok کلیک میکنیم.
از خروجی Converter Transfer به ورودی Va زیر سیستم موتورdc وصل میکنیم.
۳-۴ کنترل سیستم درایو موتور dc :
سیستم کنترل درایو موتور dc با دو حلقه فیدبک، در این فصل توضیح داده میشود. حلقه اول برای پایدارسازی جریان آرمیچر (گشتاور الکتریکی) و حلقه دوم برای پایدارسازی موتور dc استفاده میشود. سیستم کنترل موتور dc با دو کنترلکننده PI کلاسیک در شکل زیر نشان داده شده است.
خطای جیان آرمیچر، سیگنال ورودی کنترلکننده جریان است و این خطا اختلاف جریان مرجع آرمیچر و جریان واقعی آرمیچر (iaz – ia) است.
کنترلکننده سرعت و کنترلکننده جریان یک سیستم کنترل سری را تشکیل میدهند. اختلاف سرعت مرجع و سرعت واقعی (nz-ns)، خطای سرعت را تولید میکند که به عنوان سیگنال ورودی کنترلکنندهسرعت عمل میکند. خروجی کنترلکننده سرعت، سیگنال مرجع کنترل کننده جریان آرمیچر (iaz) است. لازم به ذکر است که در خورجی هر دو کنترلکننده سرعت و جریان یک محدودکننده (saturation) قرار میگیرد.
۱-۳-۴ تنظیم پارامترهای کنترل کنندههای PI کلاسیک :
Nonlineal Control Design Blockset (NCD) (به منظور برآوردن معیارهای طراحی برای سیستم با ورودی پله واحد) استفاده میشود.
همان طور که در فصل «مقدمهای بر Simulink Response Optimization»، توضیح داده شد، NCD blockkset به طور اتوماتیک معیارهای طراحی (مرزها و قیود و اطلاعات متغیرهایی که قرار است تنظیم شوند) رابه یک مسئله بهینهسازی تبدیل میکند. همان طور که میدانیم،قدم اول در راه استفاده از Simulink Response Optimization تعیین متغیرهایی است که باید تنظیم گردند. مقادیر اولیه برای این متغیرها، در سرعت بهینهسازی بسیار مهم هستند. این مقادیر اولیه را از طریق آزمون سعی و خطا تعیین میکنیم.
در مرحله بعد، مدل simUlink برای plant و کنترلکنندهها باید طراحی شوند و NCD block به سیگنالهایی که میخواهیم روی آنها قیود، قرار دهیم، وصل میشوند.
۲-۳-۴ تنظیم پارامترهای کنترل کننده جریان :
برای ساختن مدل plant در مدار حلقه جریان، از اتصالات سری تابع تبدیل یکسوساز و تابع تبدیل مدار جریان آرمیچر استفاده میکنیم.
تابع تبدیل یکسوساز را در بخش ۲-۲-۴ به دست آوردیم. اکنون تابع تبدیل مدار جریان آرمیچر را به دست میآوریم. تابع تبدیل مدار آرمیچر را به صورت زیر توضیح میدهیم.
که در آن
گین مدار جریان آرمیچر
است.
برای مدلسازی این تابع تبدیل در simUlink فقط نیاز به یک بلوک تابع تبدیل داریم. یک بلوک Transfer Fcn (از Linear block library) به پنجره مدل کپی میکنیم. نام این بلوک را به Transfer Current armiture تغییر میدهیم. روی ابن بلوک دوبار کلیک راست میکنیم تا پنجره مربوط به آن باز شود. در این پنجره در بخش مربوط به Num، «kia» و در بخش مربوط به den، [Ta ۱] را وارد میکنیم. سپس روی ok کلیک میکنیم تا نتایج ثبت شوند.
حالا میخواهیم کنترلکننده جریان را مدلسازی کنیم. این کنترلکننده، یک کنترلکننده PI است پس معادله آن مطابق رابطه زیر است.
برای مدلسازی این تابع تبدیل در simUlink یک زیر سیستم با نام Regulator-I ایجاد میکنیم. در این زیرسیستم به این ترتیب عمل میکنیم.
دو بلوک Gain، (از Linear block library) به پنجره مدل خود کپی میکنیم. نام یکی از آنها را kp۱ مینامیم و همچنین مقدار آن را نیز به kp1 تغییر میدهیم. نام بلوک Gain دیگر را ki1 مینامیم و مقدار آن را نیز به ki1 تغییر میدهیم. یک بلوک انتگرالگیر (از Linear block library) به مدل کپی میکنیم دو بلوک جمعکننده (SUM) (از Linear block library) به مدل کپی میکنیم و علامتهای یکی از آنها را به صورت «+ -» و علامت دیگری را به صورت «+ + »تغییر میدهیم.
بلوک sum که علامت آن رابه صورت «+ -» تنظیم شده است را در ابتدای مدل قرار میدهیم. خروجی آن را به ورودی گینهای kp1 و ki1 وصل میکنیم. خروجی گین kp1 را به ورودی sum دوم وصل میکنیم، خروجی گین ki1 را به ورودی انتگرالگیر وصل میکنیم و خروجی انتگرالگیر را به ورودی دیگر sum دوم وصل میکنیم.
دو بلوک ورودی (In) (از Linear block library) و یک بلوک خروجی (Out) (از Linear block library) به پنجره مدل کپی میکنیم. نام یکی از بلوکهای ورودی را به Iaz تغییر میدهیم و آن را به ورودی با علامت مثبت بلوک SUM اول وصل میکنیم. نام بلوک ورودی دیگر را به Ia تغییر میدهیم و آن را به ورودی با علامت منفی بلوک SUM اول وصل میکنیم.
خروجی بلوک SUM دوم را به بلوک خروجی (Out) وصل میکنیم. نام این بلوک خروجی را «V» مینامیم. اکنون آماده ایجاد زیرسیستم کنترلکننده جریان هستیم. گزینه Edit>select all را از پنجره مدل انتخاب میکنیم سپس Edit>Creat Subsystem را انتخاب میکنیم. زیر سیستم ایجاد شده را Regulator-I مینامیم.
مدلی با نام Current controller ایجاد میکنیم و زیرسیستم Regulator-I و تابع تبدیل یکسوساز، تابع تبدیل مدار جریان آرمیچر را به آن کپی میکنیم.
زیرسیستم Regulator-I رادر ابتدا قرار میدهیم، خروجی آن را به ورودی تابع تبدیل یکسوساز وصل میکنیم خروجی تابع تبدیل یکسوساز را به ورودی تابع تبدیل مدار جریان آرمیچر وصل میکنیم. از خروجی تابع تبدیل مدار جریان آرمیچر به ورودی Ia زیرسیستم Regulator-I وصل میکنیم.
یک بلوک step (از source library) و یک بلوک NCD (از Simulink Response Optimization) به مدل کپی میکنیم. بلوک step را به ورودی Iaz زیر سیستم Regulator-I وصل میکنیم. از خروجی تابع تبدیل مدار جریان آرمیچر به ورودی بلوک NCD وصل میکنیم.
اکنون که plant مربوط به کنترلکننده جریان آماده شد، میتوانیم برای تنظیم پارامترهای kp1 و ki1 از «Simulink Response Optimization » استفاده کنیم.
اولین قدم، وارد کردن پارامترهای مدل در « MATLAB Work space » است.
مقادیر اولیه برای kp1 و ki1 (که از آزمون سعی و خطا بدست آمدهاند) به ترتیب عبارتند از kp1=0.01 و ki1=0.5 . این مقادیر را به همراه kp=100، Tmip=0.02، Ta=0.0205 در «Work space MATLAB» وارد میکنیم.
روی NCD block دوبار کلیک میکنیم. تا پنجره مربوط به آن باز شود. درانتهای این پنجره Checkbox Enforce Signal bounds را انتخاب میکنیم.
از منوی Optimization گزینه Tuned parameter را انتخاب میکنیم و هنگامی که پنجره مربوط به parameter Tuned باز شد، روی button Add در سمت پایین و چپ این پنجره کلیک میکنیم. با این کار لیستی از پارامترهایی که ما در MATLAB workspace وارد کردهایم (یعنی kp ،Tmip، kia ،Ta،ki1 ، ki2 ) ظاهر میشود. در این لیست ما، ki1 ، ki2، را انتخاب میکنیم. (به عنوان پارامترهایی که قرار است تنظیم شوند) و سپس ok میکنیم. با این کار این دو پارامتر جز لیست Tuned parameter که در سمت چپ پنجره مربوطه قرار دارد، قرار میگیرند. مشخصات این پارامترها را که در سمت راست این پنجره Tuned parameter قرار دارند، به صورت زیر اصلاح میکنیم.
در مورد پارامتر kp1 ، مقدار ماکزیمم آن را به ۰۵.۰ و مقدار مینیمم آن را به صفر تغییر میدهیم و در مورد پارامتر ki1 ، مقدار ماکزیمم آن را به ۶.۰ و مقدار مینیمم آن را به ۴.۰ تغییر میدهیم.
در پایان در پنجره Tuned parameter روی button ok کلیک میکنیم تا تنظیمات انجام شده، save گردد.
حالا به سراغ تنظیم قیود setting time، over shoot، rise time میرویم.
از منوی Goals گزینه Desired Response را انتخاب میکنیم. پنجرهای باز میشود که ما در آن گزینه specify step response characteries را انتخاب میکنیم که با این کار پنجره مربوط به تنظیمات پاسخ بله ظاهر میشود. در این پنجره اصلاحات زیر را انجام میدهیم.
- در قسمت مربوط به ورودی بله زمان «step time» را به ۰۰۲.۰، صفر تغییر میدهیم.
- rise time را به ۰۲۵.۰ تغییر میدهیم.
- setting time را به ۰۷۵.۰ تغییر میدهیم.
- over shoot را به ۲% تغییر میدهیم.
- Setting% را به ۰۰۰۵.۰ تغییر میدهیم.
سپس روی ok کلیک میکنیم تا تنظیمات save گردد.
حالا که پارامترهای تنظیمپذیر را تعیین کردیم و پاسخ بله مطلوب را تعیین کردیم، میتوانیم بهینهسازی (Optimization) را شروع کنیم. قبل از شروع بهینهسازی دقت میکنیم که بلوک step موجود در مدل simUlink نیز باید دارای step time =0.002 باشد.
با انتخاب optimization>simulation optimization، پنجره مربوط به تنظیمات شبیهسازی را انتخاب میکنیم و در آن stop time را به ۵.۰ تغییر میدهیم. روی دکمه ok کلیک کرده و سپس optimization>start را انتخاب میکنیم تا بهینهسازی run شود. در حین بهینهسازی، نمودار اولیه به رنگ آبی، نمودارهای میانی به رنگهای مختلف و نمودار نهایی به رنگ سفید رسم میشود.
همچنین پنجره progress window نتیجه محاسبات برای ki1 ، kp1 ، را به صورت زیر نشان میدهد.
kp1=0.018
ki1=۰٫۳۹۵۵
در پایان برای اطمینان از نتیجه حاصل شده Simulation را با مقادیر =۰٫۰۱۸ kp1 و ki1=0.3955، run میکنیم. که نتایج به صورت زیر است که حاکی از درستی محاسبات است.
در این جا می خواهیم کمی بیشتر در مورد کنترلکننده PI که در مدل استفاده کردهایم، توضیح دهیم.
نخستین موضوع مهم که باید به آن پرداخته شود بحث پایداری سیستم کنترلکننده جریان است. برای بحث پایدار بودن و یا پایدار نبودن سیستم از معیار روث-هوروتیز به صورت زیر استفاده میکنیم:
در سیستم کنترلکننده جریان، G۱ را تابع حلقه باز و T1 را تابع تبدیل حلقه بسته مینامیم به این ترتیب داریم:
به این ترتیب معادله مشخصه سیستم به صورت زیر است.
اکنون جدول راث-هورویتز را تشکیل میدهیم.
| Kp1 ×kia×۱+kp | Ta ×Tmip | S3 |
| Ki1×kia×kp | Tmip+Ta | S2 |
| ۰ | b1 | S1 |
| Ki1×kia×kp | S0 |
که در آن
است. همان طور که میدانیم معیار پایداری راث-هوریتز این است که در ستون اول تغییر علامت نداشته باشیم. از آنجایی که Ta، Tmip، kp، kia همگی مثبت هستند برای پایداری باید دو شرط زیر را داشته باشیم.
- ki1>0
- b1>0 و در نتیجه
با جایگزین کردن kia، kp، Tmip و Ta داریم :
اکنون با جایگزینی kp1=0.018 و ki1=0.3955 داریم :
که از ۰۰۰۴۱/۰ بزرگتر است پس به ازای این مقادیر سیستم پایدار است.
حالا میخواهیم اثر کنترل کننده تناسبی و کنترل کننده تناسبی-انتگرالی را جداگانه بررسی کنیم. برای این منظور، ابتدا در کنترل کننده جریان فقط از ترم تناسبی استفاده میکنیم. M-file به صورت زیر مینویسیم:
Kp=100;
Tmip=0.02;
Kia=1.282;
Ta=0.0205;
num=kp*kia
den=[(Tmip*Ta) (Tmip+Ta) (۱)];
motor=tf (num,den);
Kp1=0.018;
Contr=kp1;
sys_cl=feedback(contr*motor,1);
t=0:0.002:0.5;
step(sys_cl,t);
title(‘Step Response With Proportional Control‘)
m-file را run میکنیم. Plot زیر را مشاهده میکنیم:
همان طور که در plot بالا مشاهده میکنیم، خطای حالت ماندگار داریم، بنابراین برای از بین بردن خطای حالت ماندگار ترم انتگرالگیر را به کنترلکننده اضافه میکنیم.
m-file به صورت زیر ایجاد میکنیم:
Kp=100;
Tmip=0.02;
Kia=1.282;
Ta=0.0205;
num=kp*kia
den=[(Tmip*Ta) (Tmip+Ta) (۱)];
motor=tf(num,den);
Kp1=0.018;
Ki1=0.3955;
Contr=tf([kp1 ki1] , [1 ۰]);
sys_cl=feedback(contr*motor,1);
t=0 : 0.002 : 0.5;
Step(sys_cl,t);
title(‘PI Control With kp1 & ki1’)
m-file را run میکنیم. Plot زیر را مشاهده میکنیم:
همان طور که در plot بالا مشاهده میکنیم، پاسخ شرایط مطلوب را دارد و خطای حالت ماندگار از بین رفته است.
اکنون میخو اهیم مکان هندسی کنترلکننده جریان به همراه کنترلکننده آن را رسم کنیم. کاری که میخواهیم در اینجا انجام دهیم این است که روی مکان هندسی ریشهها، مقادیر k، و پاسخ بله مربوط به این مقدار k را رسم میکنیم. برای این منظور m-file زیر را ایجاد میکنیم:
Kp=100;
Tmip=0.02;
Kia=1.282;
Ta=0.0205;
num=kp*kia
den=[(Tmip*Ta) (Tmip+Ta) (۱)];
motor=tf(num,den);
Kp1=0.018;
Ki1=0.3955;
Contr=tf([kp1 ki1] , [1 ۰]);
rlocus(motor*contr);
[k,poles]=rlocfind(motor*contr);
sys_cl=feedback(k*motor*contr,1);
t=0 : 0.002 : 0.5;
Step(sys_cl,t);
title(‘Step Response With Controller’)
m-file را run میکنیم. Plot زیر را مشاهده میکنیم:
در مکان هندسی ریشهها بااستفاده از خطوط قطری نقطهدار میتوانیم k و پاسخ بله مربوط به آن را ببینیم با انتخاب k های مختلف و دیدن پاسخهای مربوط به آن ما k=0.5312 را انتخاب میکنیم که قطبهای مربوط به این مقدار k عبارتند از i9130.48+5284.41- و i9130.48-5284.41- و پاسخ بله مربوط به آن به صورت زیر است:
۳-۳-۴ تنظیم پارامترهای کنترل کننده سرعت :
یک مدل plant، برای مدار حلقه سرعت با اتصال سری تابعهای حلقه جریان که در بخش قبلی طراحی شد و سیستم مکانیکی ساخته میشود.
تابع تبدیل موتور و بارش به صورت زیر است:
که در آن
، گین مدار سرعت
، ثابت زمانی الکترومکانیکی است.
برای مدلسازی تابع تبدیل موتور در simUlink، یک بلوک transfer Fcn (از Linear block library) به پنجره مدل کپی میکنیم. با دو بار کلیک راست کردن روی این بلوک، پنجره مربوط به ان را باز میکنیم، و در قسمت مربوط به Num، عدد ۰۱۲۷.۰ که مربوط به گین مدار سرعت است را وارد میکنیم و در قسمت مربوط به den، اعداد [۱ ۵] که مربوط به Tm است را وارد میکنیم. سپس روی ok کلیک میکنیم.
اکنون باید کنترلکننده سرعت، که یک کنترلکننده PI است را پیادهسازی کنیم. همان طور که در بخش کنترلکننده جریان گفته شد، یک زیر سیستم با نام Regulator-n میسازیم به این ترتیب:
دو بلوک Gain (از Linear block library)، یک بلوک انتگرالگیری و دو بلوک جمعکننده (SUM) (از Linear block library) به پنجره مدل کپی میکنیم.
یکی از بلوکهای گین را kp2 مینامیم و مقدار آن را نیز به kp2 تغییر میدهیم.
بلوک گین دیگر را ki2 مینامیم و مقدار آن را نیز به ki2 تغییر میدهیم.
یک بلوک SUM در ابتدای مدل قرار میدهیم. علامت آن را به صورت «- +» اصلاح میکنیم. از خروجی به ورودی بلوکهای گین kp2 و ki2 وصل میکنیم. بلوک SUM بعدی را در ادامه مدل قرار میدهیم و علامت آن را به صورت «+ +» اصلاح میکنیم. خروجی گین kp2 را به یکی از ورودیهای این بلوک SUM وصل میکنیم. خروجی گین ki2 را به ورودی بلوک انتگرالگیر وصل میکنیم و خروجی بلوک انتگرال گیر را به ورودی دوم بلوک SUM (بلوک SUM دومی) وصل میکنیم.
دو بلوک ورودی (In) و یک بلوک خروجی (Out) (از Linear block library) به پنجره مدل کپی میکنیم. یکی از بلوکهای ورودی را nz مینامیم و آن را به ورودی مثبت بلوک SUM اولی وصل میکنیم. بلوک ورودی دیگر را ns مینامیم و آن را به ورودی منفی بلوک SUM اولی وصل میکنیم. بلوک خروجی (Out) را Iaz مینامیم و خروجی بلوک SUM دومی را به ورودی این بلوک وصل میکنیم.
اکنون زیرسیستم Regulator-n را ایجاد میکنیم.
از منوی Edit گزینه select all را انتخاب میکنیم. سپس Edit>Creat subsystem را انتخاب میکنیم. به این ترتیب زیر سیستم مربوطه ایجاد میشود. ما نام این زیر سیستم را به Regulator-n تغییر میدهیم.
برای مدلسازی plant کنترلکننده سرعت، یک پنجره مدل با نام speed controller ایجاد میکنیم. زیر سیستمهای Regulator-n، Regulator-n، تابع تبدیل یکسوساز، موتور مدار جریان آرمیچر را به این مدل کپی میکنیم. همچنین یک بلوک step (از Source library) و یک بلوک NCD (از Simulink Response Optimization) به مدل کپی میکنیم.
خروجی بلوک step رابه ورودی nz از زیر سیستم Regulator-n وصل میکنیم. خروجی زیرسیستم Regulator-n را به ورودی Iaz از زیر سیستم Regulator-I وصل میکنیم. از خروجی زیر سیستم Regulator-I یک خط به ورودی تابع تبدیل یکسوساز وصل میکنیم. از خروجی تابع تبدیل یکسوساز به ورودی تابع تبدیل مدار آرمیچر وصل میکنیم. از خروجی تابع تبدیل مدار آرمیچر یک خط به ورودی Ia از Regulator-I وصل میکنیم و یک خط به ورودی تابع تبدیل موتور وصل میکنیم. از خروجی تابع تبدیل موتور یک خط به ورودی ns از Regulator-n وصل میکنیم. و یک خط به ورودی بلوک NCD وصل میکنیم.
اکنون که plant کنترلکننده سرعت آماده شد، میتوانیم از Simulink Response Optimization برای تنظیم پارامترهای kp2 و ki2 استفاده کنیم.
اولین قدم در این راه، وارد کردن پارامترهای مدل در «Work space MATLAB» است. مقادیر اولیه برای kp2 و ki2 از آزمون سعی و خطا به دست میآید. این مقادیر عبارتند از kp2=1 و ki2=2.5. این مقادیر را به همراه kp=100، Tmip=0.02، kia=1.282 و Ta=0.0205، kp1=0.018، ۰٫۳۹۵۵=ki1در «Work space MATLAB» وارد میکنیم.
روی بلوک NCD دوبار کلیک میکنیم تا پنجره مربوط به آن باز شود.درانتهای این پنجره Check box Enforce Signal bounds را انتخاب میکنیم.
از منوی Optimization گزینه Tuned parameter را انتخاب میکنیم و هنگامی که پنجره مربوط به parameter Tuned باز شد، روی button Add در سمت پایین و چپ این پنجره کلیک میکنیم. با این کار لیستی از پارامترهایی که ما در MATLAB workspace وارد کردهایم (یعنی kp ،Tmip، kia ،Ta،ki1 ،kp1، ki2 ، kp2) ظاهر میشود. در این لیست، kp2 ، ki2، را انتخاب میکنیم. (به عنوان پارامترهایی که قرار است تنظیم شوند) و سپس ok میکنیم. با این کار این دو پارامتر جز لیست Tuned parameter (که در سمت چپ این پنجره قرار گرفته)، قرار میگیرند. مشخصات این پارامترها را که در سمت راست این پنجره Tuned parameter قرار دارند، به صورت زیر اصلاح میکنیم.
در مورد پارامتر kp2 ، مقدار ماکزیمم آن را به ۲ و مقدار مینیمم آن را به ۹.۰ تغییر میدهیم و در مورد پارامتر ki2 ، مقدار ماکزیمم آن را به ۵ و مقدار مینیمم آن را به ۲ تغییر میدهیم.
در پایان در پنجره Tuned parameter روی ok کلیک میکنیم تا تنظیمات انجام شده، save گردد.
حالا به سراغ تنظیم قیود setting time، over shoot، rise time میرویم.
از منوی Goals گزینه Desired Response را انتخاب میکنیم. پنجرهای باز میشود که ما در آن گزینه specify step response characteries را انتخاب میکنیم که با این کار پنجره مربوط به تنظیمات پاسخ بله ظاهر میشود. در این پنجره اصلاحات زیر را انجام میدهیم.
- در قسمت مربوط به ورودی بله زمان «step time» را به ۰۰۲.۰، صفر تغییر میدهیم.
- rise time را به ۰۵.۰ تغییر میدهیم.
- setting time را به ۱۵.۰ تغییر میدهیم.
- over shoot را به ۲% تغییر میدهیم.
- Setting% را به ۰۰۰۵.۰ تغییر میدهیم.
سپس روی ok کلیک میکنیم تا تنظیمات save گردد.
حالا که پارامترهای تنظیمپذیر را تعیین کردیم و پاسخ بله مطلوب را نیزتعیین کردیم، بهینهسازی را run میکنیم. قبل از شروع بهینهسازی دقت میکنیم که بلوک step موجود در مدل simUlink نیز باید دارای step time =0.002 باشد.
با انتخاب optimization>simulation optimization، پنجره مربوط به تنظیمات شبیهسازی را باز میکنیم و در آن stop time را به ۵.۰ تغییر میدهیم. روی دکمه ok کلیک کرده و سپس optimization>start را انتخاب میکنیم تا بهینهسازی run شود.
در حین بهینهسازی، نمودار اولیه به رنگ آبی، نمودارهای میانی به رنگهای مختلف و نمودار نهایی به رنگ سفید رسم میشود.
همچنین progress window نتیجه محاسبات برای kp2 ، ki2 ، را به صورت زیر نشان میدهد.
Kp2=1.1909 ki2=1.9129
در پایان برای اطمینان از نتیجه حاصل شده Simulation را با مقادیر Kp2=1.1909 و Ki2=1.9129، run میکنیم. نمودار زیر حاکی از درستی محاسبات است.
در این جا می خواهیم کمی بیشتر در مورد کنترلکننده PI که در مدل استفاده کردهایم، توضیح دهیم.
نخستین موضوع مهم که باید به آن پرداخته شود بحث پایداری سیستم است. در این مورد از معیار راث-هوروتیز استفاده میکنیم.
G1 تابع تبدیل حلقه باز سیستم کنترل کننده جریان است.
T1 تابع تبدیل حلقه بسته کنترلکننده جریان است.
G2 تابع تبدیل حلقه باز سیستم کنترکننده سرعت است.
T2 تابع تبدیل حلقه بسته، سیستم کنترلکننده سرعت است.
در نتیجه معادله مشخصه سیستم کنترلکننده سرعت، به صورت زیر محاسبه میشود:
برای پایداری در ستون اول تغییر علامت نباید داشته باشیم. جدول راث هورویتز را تشکیل میدهیم:
| ۲٫۳۱+۰٫۰۲۹ki2+۰٫۶۴۵kp2 | ۳٫۳۴۸ | ۰٫۰۰۲۰۵ | S5 |
| ۰٫۶۴۴ki2 | ۲۵۶٫۸۳+۰٫۰۲۹kp2 | ۰٫۲۰۹۱ | S4 |
| ۰ | b | a | S3 |
| ۰ | ۰٫۶۴۴ki2 | c | S2 |
| ۰ | d | S1 | |
| ۰٫۶۴۴ki2 | S0 |
که در آن :
اگر kp2=1.1901 و ki2=1.9129 را جایگزین کنیم ومقادیر a و b و c و d را محاسبه کنیم نتایج به صورت زیر خواهد بود.
a=0.825 , b=5.81 , c=255.39 , d=0.996
همان طور که مشاهده میکنیم به ازای مقادیر محاسبه شده برای kp2 و ki2 یعنی kp2=1.1901 و ki2=1.9129 تمام a و b و. C و d مثبت هستند. یعنی در ستون اول جدول راث- هورویتز تغییر علامت نداریم و بنابراین سیستم کنترل سرعت پایدار است.
اکنون میخواهیم اثر کنترلکننده تناسبی و انتگرالی را به صورت جداگانه بررسی میکنیم. بنابراین در کنترلکننده سرعت مقدار kp2 را ۱۹۰۹.۱ و مقدار ki2 را صفر قرار میدهیم. Simulation را run میکنیم. نمودار حاصل به صورت زیر خواهد بود:
همان طور که میبینیم در نمودار بالا خطای حالت ماندگار وجود دارد. بنابراین برای از بین بردن آن ترم انتگرالی را به کنترل کننده تناسبی اضافه میکنیم. یعنی ki2 را از صفر به ۹۱۲۹.۱ تغییر میدهیم دوباره Simulation را run میکنیم. نمودار حاصل به صورت زیر خواهد بود:
همان طور که میبینیم خطای حالت ماندگار در نمودار بالا، از بین رفته است.
حالا که کنترل کننده سرعت و جریان را جداگانه طراحی کنیم. باید این کنترلکنندهها را در plant اصلی قرار دهیم.
۴-۴- plant اصلی :
زیرسیستمهای کنترل کننده جریان و سرعت را به پنجره مدل کپی میکنیم. همچنین زیر سیستم موتور و تابع تبدیل یکسوساز را نیز به پنجره مدل کپی میکنیم. دو بلوک ثابت، دو بلوک step برای ورودیهای wz (از زیرسیستم کنترلکننده سرعت) و TL (از زیرسیستم کنترلکننده جریان)، دو بلوک workspace to، یک بلوک clock دو بلوک manual switch به پنجره مدل کپی میکنیم.
زیرسیستم کنترلکننده سرعت ار در ابتدا قرار میدهیم. یک بلوک ثابت و یک بلوک step را طوری قرار میدهیم که به وسیله manual switch بتوانیم بین این دو مقدار عمل Switch را انجام دهیم. خروجی بلوک manual switch را به ورودی wz از زیرسیستم کنترلکننده سرعت وصل میکنیم.
خروجی زیرسیستم کنترلکننده سرعت را به ورودی Iaz زیرسیستم کنترلکننده جریان وصل میکنیم. خروجی زیر سیستم کنترل کننده جریان را به ورودی تابع تبدیل یکسوساز وصل میکنیم. خروجی تابع تبدیل یکسوساز را به ورودی Va از زیرسیستم موتور وصل میکنیم.
یک بلوک ثابت، یک بلوک step را طوری قرار میدهیم که به وسیله manual switch بتوانیم بین این دو مقدار Switch کنیم. خروجی manual switch را به ورودی TL، زیرسیستم موتور وصل میکنیم. خروجی w زیرسیستم موتور را به ورودی ws، زیرسیستم کنترلکننده سرعت وصل میکنیم، خروجی Ia زیرسیستم موتور را به ورودی Ia از زیر سیستم کنترلکننده جریان وصل میکنیم.
از خروجی w زیرسیستم موتور یک خط به ورودی بلوک To workspace وصل میکنیم. پنجره مربوط به این بلوک را باز میکنیم. نام این بلوک را به w تغییر میدهیم و در قسمت structure گزینه array را انتخاب میکنیم. بلوک clock را نیز به بلوک workspace To دیگر وصل میکنیم. نام این بلوک workspace To را به t تغییر میدهیم و در قسمت structure گزینه array را انتخاب میکنیم.
اکنون باید مقادیر kp1=0.018 و ki1=0.3955 و kp2=1.1909 و ki2=1.9129 ، این مدل simUlink را Run میکنیم. فراموش نمیکنیم که برای سرعت مرجع و گشتاور بار باید ورودی ثابت یا بله را انتخاب کنیم. نمودار سرعت برای چند سرعت مرجع در زیر نشان داده شده است:
خروجی متلب:
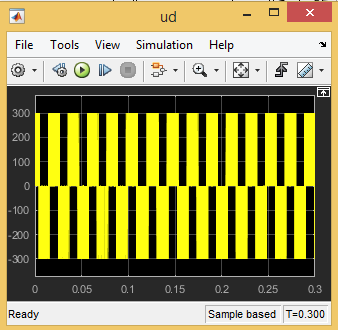
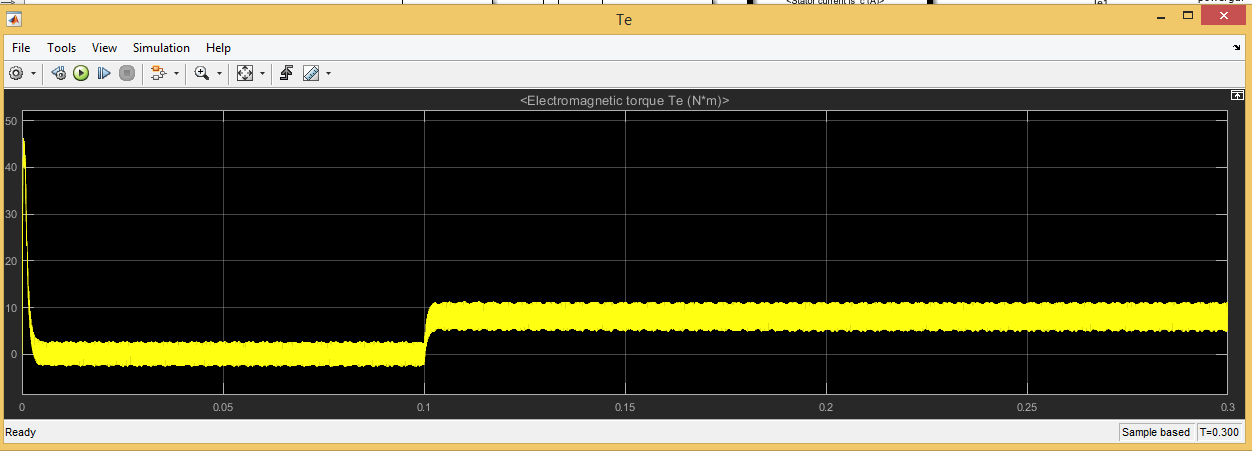
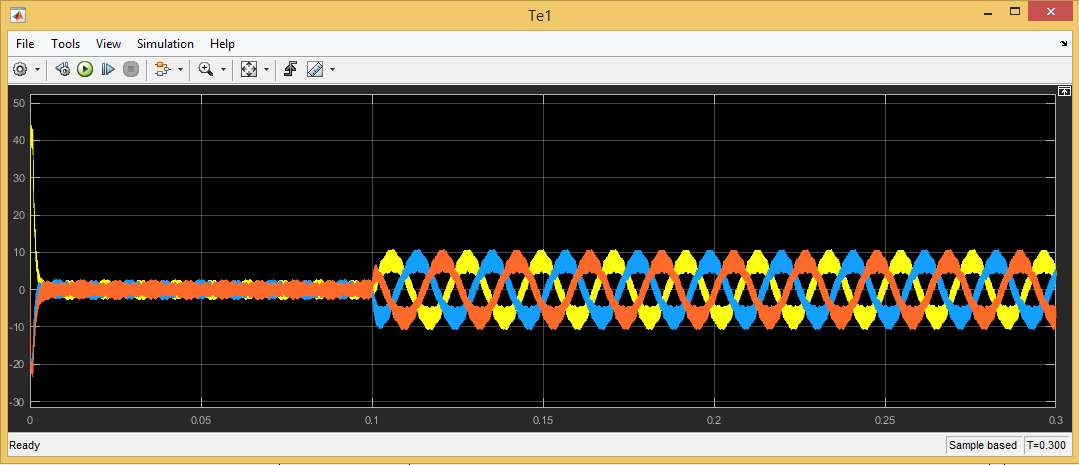
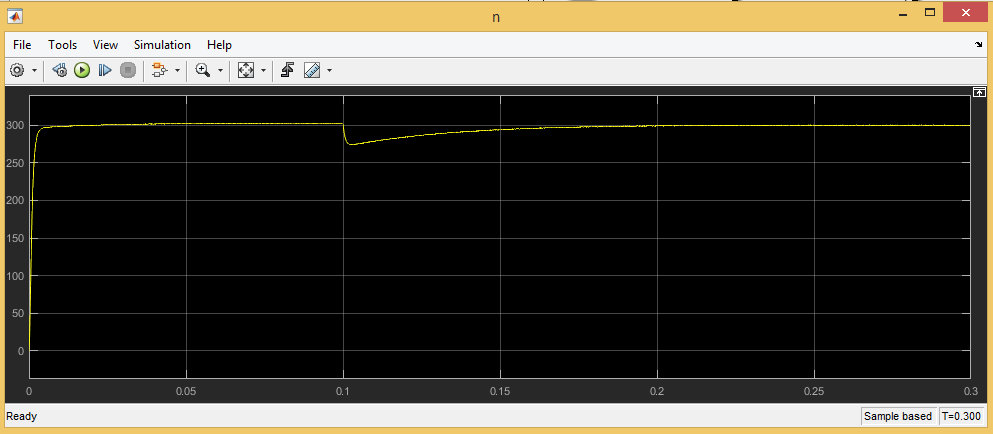
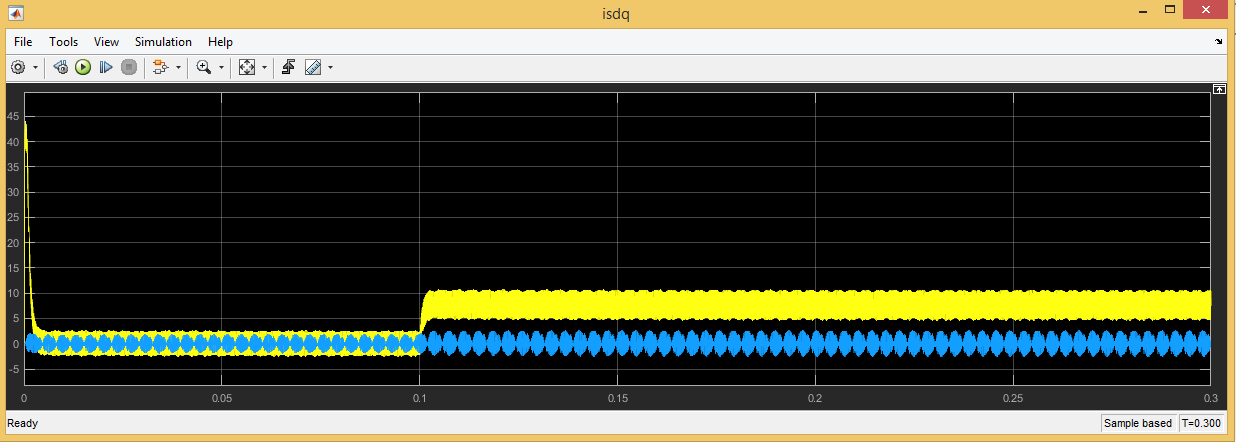
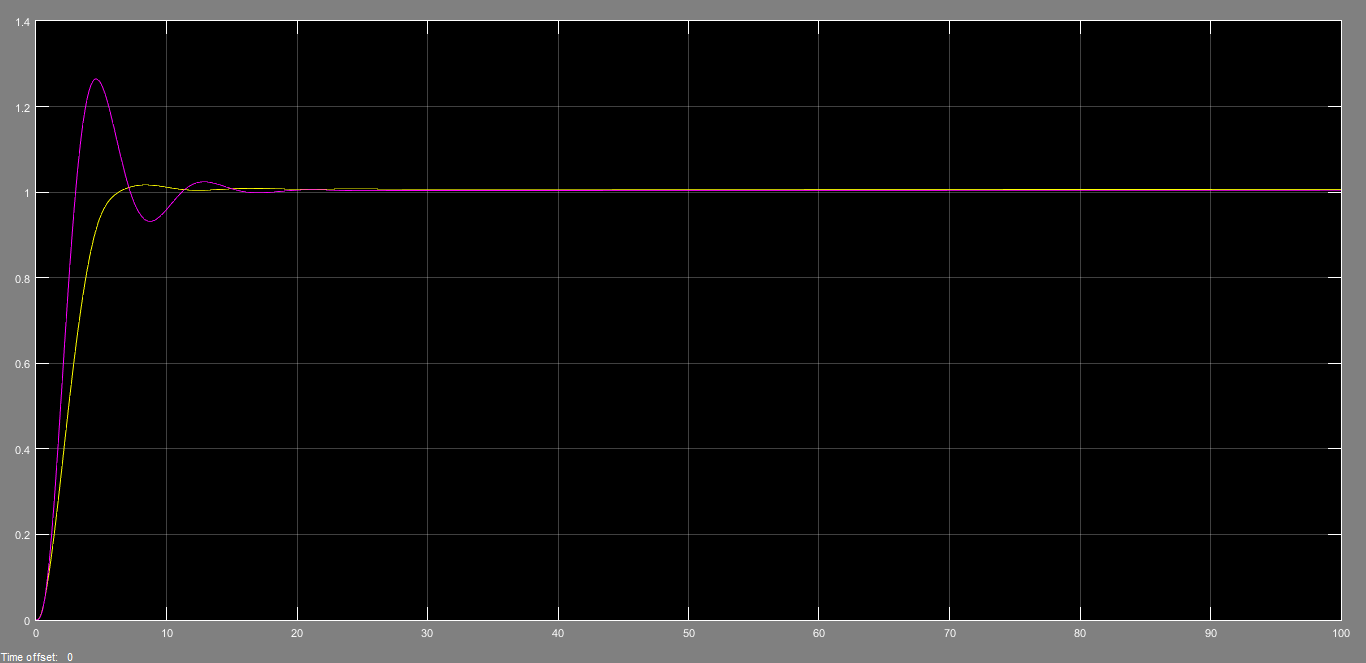

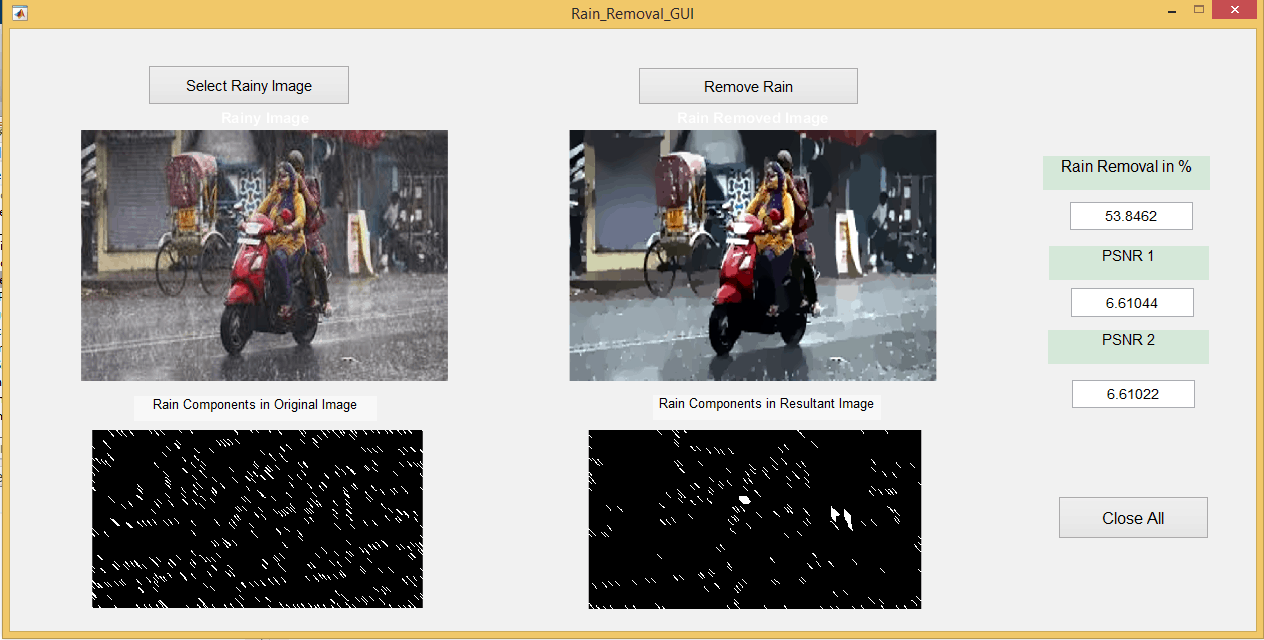

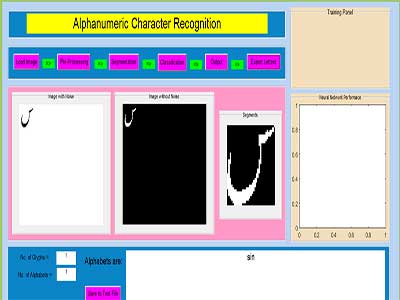
لطفاً براي ارسال دیدگاه، ابتدا وارد حساب كاربري خود بشويد