حل معادله فاکنر اسکن Falkner Skan در متلب
حل معادله فاکنر اسکن Falkner Skan در متلب :پروژه متلب
پروژه متلب در این پروژه با کمک متلب معدله فاکنر اسکن را حل کرده ایم و میتوانید با تغییر پارامترهای معادله
پروژه متلب در این پروژه یک روش تحلیلی ، روش هموتوپی-پرتوربیشن ، برای حل معادلات حاکم بر لایه مرزی دو بعدی برای سیال تراکم ناپذیر به کار برده شده است. این روش یکی از روش های تحلیلی برای حل معادلات غیر خطی است . مزیت استفاده از روش هموتوپی- پرتوربیشن، برطرف کردن محدودیت های دو روش هموتوپی و پرتوربیشن کلاسیک میباشد. در کار حاضر، معادله فالکنر- اسکن برای شرایط خاص ( جریان بلازیوس، جریان نقطه سکون) حل شده است.
پروژه متلب مشاهده شد که این روش نتایج بسیار دقیقی به دست میدهد و همچنین یک ابزار قدرتمند ریاضی است که برای حل مسایل زیاد خطی و غیر خطی در شاخههای مختلف علوم و مهندسی مخصوصاً برخی معادلات مکانیک سیالات به کار برده میشود. پروژه متلب در حال حاضر سعی شده است یک تکنیک خاصی استفاده گردد که توانستیم نتایجی را که خیلی نزدیک به نتایج دقیق معادله است به دست آوریم. مقایسه جوابها با جوابهای حاصل از روشهای دیگر نشان میدهد که تطابق بسیار خوبی برقرار است،پروژه متلب دقت بالا و سهولت محاسبات از مزایای مهم این روش میباشد.
اگر تابعی از متغیر حقیقی باشد و ضابطه آن و متغیر تابع یا مقدار تابع باشد، آنگاه مشتق با یکی از نمادهاینمایش داده می شود. همچنین مشتق دوم، سوم،… و ام آن نیز به ترتیب با نمادهای
نمایش داده می شوند. اگر تابعی از دو متغیر حقیقی باشد آنگاه مشتق های جزئی با نمادهای نمایش داده می شوند. همچنین اگر آنگاه مشتق های جزئی با نمادهای و یا نمایش داده می شوند.
همچنین داریم:
که این توابع مشتقات جزئی مرتبه دوم و مراتب بالاتر است.
همچنین برای توابع متغیر حقیقی داریم:
که فرض می کنیم همه مشتقات جزئی تا مرتبه مورد نظر پیوسته باشند.
حال برای تابع از متغیر حقیقی با مقدار حقیقی را دیفرانسیل تابع گویند. اگر تابع از متغیر حقیقی باشد. را دیفرانسیل کامل تابع گویند. که در حالت خاص اگر از دو متغیر حقیقی با مقدار حقیقی باشد داریم:
معادلات دیفرانسیل معمولی و با مشتقات جزئی
یک معادله دیفرانسیل هر کدام از توابع ضمنی از متغیر یا متغیرهای مستقل، متغیر یا متغیرهای تابع و مشتق های متغیر یا متغیر های تابع نسبت به متغیر یا متغیرهای مستقل می تواند باشد که حتماً باید لا اقل یک مشتق ساده یا جزئی در آن حضور داشته باشد.
معادله دیفرانسیل یک نوع از معادلات دیفرانسیل است که فقط یک متغیر مستقل در آن وجود دارد. و متغیر تابع و مشتقات مرتبه اول تا ام نسبت به است. متغیر می توانند در معادلات دیفرانسیل نباشند ولی حضور لااقل یک مشتق الزامی است. معادله دیفرانسیل یک نوع معادله است که شامل متغیر مستقل است و فقط یک متغیر تابع دارد که در آن تابعی از ها است.
برای دسته بندی معادلات دیفرانسیل می گوییم هرگاه همه مشتق های ظاهر شده در معادله مشتق ساده باشند آنگاه معادله را معادله دیفرانسیل معمولی (یا ساده یا عادی) می نامیم. اما اگر در عبارت معادله لااقل یک مشتق جزئی ظاهر شود آن را یک معادله دیفرانسیل با مشتقات جزئی یا معادله دیفرانسیل نسبی می نامیم.
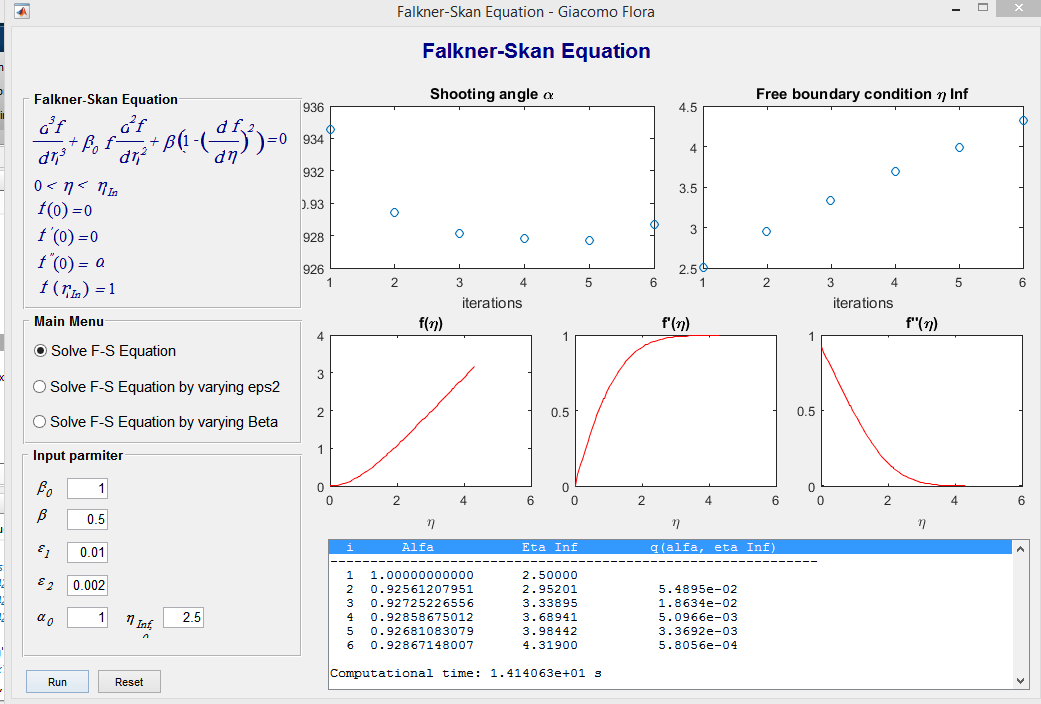
خروجی متلب :
دیدگاه ها